Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Одним из основных источников питания высокогорных рек и озер является ледниковый сток; его объем и распределение во времени определяют гидрологический режим водных объектов. С начала XXI в. многие горные ледники реагируют на глобальное потепление сокращением площадей поверхности и объемов. При этом таяние ледников приводит к образованию прорывоопасных озерно-ледниковых комплексов в районах деградации оледенения. Зачастую для решения широкого спектра задач в рамках водопользования, прогнозов состояния водных ресурсов и обеспечения безопасности горных регионов необходимы оценки величин стока с водосборов, имеющих оледенение.

Для расчета стока с ледников часто используются региональные зависимости, в основу которых положены данные измерений абляции. Последние проводятся эпизодически и далеко не на всех ледниках. Возможность использования эмпирических формул часто ограничена конкретным регионом, а создание новых требует обширных данных фактических наблюдений. В этом случае целесообразно применение математических моделей, основанных на физических закономерностях, не зависящих от конкретного горного региона. В условиях недостатка данных (регулярные гидрометеорологические наблюдения приурочены к редким метеостанциям или постам, чаще всего расположенным значительно ниже по высоте) алгоритм модели должен использовать относительно легко определяемую исходную информацию об объекте, а также рассчитывать сток с любого ледника с минимально возможной погрешностью.

В настоящее время наибольшее применение имеют модели, основанные на уравнениях теплового баланса [1–4]. Среди них – уравнение П.П. Кузьмина [5, с. 235], применимое как для расчета таяния снега, так и для моделирования ледникового стока, а также модель A-melt, которая показала хорошую сходимость результатов рассчитанных и измеренных значений абляции при расчете стока ледникового бассейна Джанкуат на Кавказе [6].

Целью данной работы является тестирование алгоритмов расчета величин талого ледникового стока в условиях недостатка данных на примере ледника Некрасова (Алтай).

Материалы и методы исследования

Объектом исследования, на примере которого выполнены расчеты, является карово-долинный ледник Некрасова, расположенный на территории Южно-Чуйского хребта Центрального Алтая (рис. 1). Его площадь составляет 0,91 км2, средняя высота – 3000 м.

Для оценки поверхностной абляции ледника производились измерения по деревянным рейкам (12 реек, длиной 1,5 и сечением 40 × 15 мм), которые были размещены в узлах сетки близкой к регулярной, покрывающей зону абляции ледника (рис. 2). Абляционные рейки устанавливались на характерных для ледника участках. Отсчеты снимались с помощью рулетки с точностью 0,5 см (погрешность 0,25 см) 1 раз в сутки с лицевой и обратной стороны рейки с последующим осреднением. С 12 (начало наблюдений) до 15 июля работы производились на рейках 1–8 (рис. 2), после чего были забурены рейки 9–12. Отсчеты по всем 12 рейкам продолжались до 29 июля.

В настоящей статье были рассмотрены два алгоритма расчета слоя таяния ледника. В основе первого лежит уравнение теплового баланса, представленное в модели A-melt [6]. Второй алгоритм основан на уравнении теплового баланса в форме, предложенной П.П. Кузьминым [5, с. 235].

Слой абляции в обоих случаях рассчитывается на основе теплового баланса ω кал/кв.см:

А = (10ω) / L = ω / 8, (1)

где А – слой абляции (мм), L – скрытая теплота плавления льда (80 кал/г) [6].

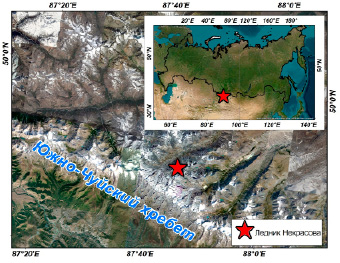
Рис. 1. Месторасположение ледника Некрасова

Рис. 2. Схема расположения абляционных реек на леднике Некрасова

Тепловая энергия ω кал/кв.см определяется с помощью уравнений теплового баланса, записанных для первого и второго случая уравнениями (2) и (3) соответственно:

ω = Sср + Еа – ЕЗ ± ωТ ± ωЛК ± QM ± S. (2)

ω = Sср + ЕЗ + Еа + ωТ, (3)

где Sср – приходная коротковолновая радиация, кал/см2; Еа – встречное излучение атмосферы, кал/см2; EЗ – длинноволновое излучение земной поверхности, кал/см2; ωТ –турбулентный теплообмен с атмосферой, кал/см2; ωЛК – скрытый поток тепла, возникающий за счет испарения, кал/см2; QM – поток тепла через чехол моренных отложений, кал/см2; S – тепло, приносимое с дождевыми осадками, кал/см2.

Несмотря на то, что оба алгоритма основаны на уравнении теплового баланса, в первом учитывается бóльшее количество составляющих (табл. 1), а также есть различия в используемых формулах и коэффициентах при их расчетах. Так, расчет суммарной приходной коротковолновой радиации различается только в использовании коэффициентов для учета нижней (NH) и общей облачности (N0). При N0 = NH формулы становятся одинаковыми. Встречное излучение атмосферы принимается как константа в первом алгоритме, но рассчитывается во втором как составляющая уравнения П.П. Кузьмина. Испарение при расчете турбулентного теплообмена определяется по формуле П.П. Кузьмина [5, с. 71]. Длинноволновое излучение поверхности рассчитывается по уравнению Стефана – Больцмана. Отметим также, что параметры с 5 по 7 (табл. 1) в уравнении П.П. Кузьмина (второй алгоритм) не учитываются.

Сумма kS’ + kDN в уравнении (10) (табл. 1) зависит от прозрачности атмосферы. Коэффициент kS’ является табличным значением (табл. 2). Коэффициент kD при наличии устойчивого снежного покрова рассчитывается по формуле (11) (табл. 1). Отношение D/S’ = (D/S)∙(1/sin hП), где D/S является табличным значением (табл. 2). Полученное значение (Q+q)0 необходимо умножить на долю светлого времени суток – DZ. Таблицы с описанными выше коэффициентами также приведены в [7, с. 130, 158–165].

Альбедо (αs) определено с помощью формулы (12) (табл. 1). Расчет по данному уравнению начинается с момента последнего снегопада. В начальный момент времени n = 0 значение альбедо будет минимальным, так как на поверхности ледника будет лежать свежевыпавший снег. В дальнейшем снег начинает стареть и его альбедо постепенно растет в экспоненциальной зависимости от количества дней с последнего выпадения снега. Влияет на альбедо и то, какая температура воздуха была на момент снегопада: при положительных ее значениях рост альбедо будет быстрее, чем при отрицательных [8, 9].

В связи с отсутствием измеренных данных на леднике при расчете принимались следующие допущения: скорость ветра при тестировании обоих алгоритмов была принята как константа (в зависимости от высоты местности, [10]); температура поверхности ледника – равной нулю, то есть температуре тающего льда; нижняя облачность равной общей. В табл. 2 приведены значения используемых при расчетах параметров.

Таблица 1

Формулы, используемые в расчетах элементов теплового баланса

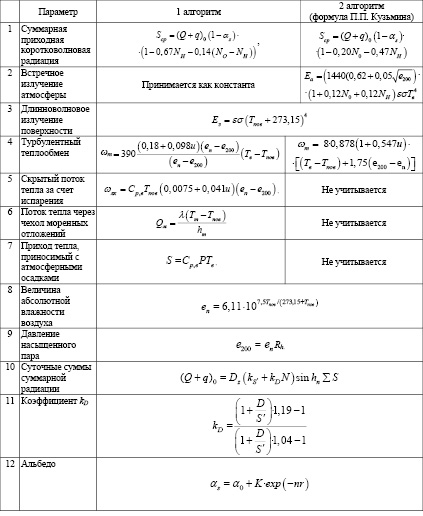
Примечание: обозначения составляющих уравнений, значения коэффициентов и констант приведены в табл. 2.

Таблица 2

Значения параметров, используемых при расчетах

Оценка сходимости рассчитанных и измеренных величин слоя таяния оценивались относительно критического коэффициента корреляции:

Ккрит = 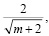(4)

где m – период, для которого производилось сравнение результатов моделирования и измерений абляции.

Результаты исследования и их обсуждение

Анализ полученных результатов показал удовлетворительную сходимость суточных слоев таяния ледника, рассчитанных с помощью обоих алгоритмов и величиной абляции по данным измерений на леднике (рис. 3). Коэффициенты корреляции К между расчетными и измеренными значениями составили 0,59 и 0,61 для первого и второго алгоритмов соответственно, что превысило в обоих случаях критическое значение коэффициента корреляции Ккрит, составляющее 0,46 (при уровне значимости α = 5%).

Ккрит =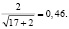

Абсолютная и относительная погрешности расчетов, средняя квадратическая ошибка оказались меньше по второй модели (табл. 3). Таким образом, несмотря на упрощенную запись уравнения теплового баланса, второй алгоритм точнее описывает таяние ледника, хотя обе модели можно считать приемлемыми.

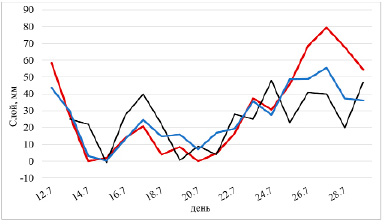
Рис. 3. Графики хода значений слоя таяния ледника Некрасова: черным цветом обозначены измеренные значения 12–29 июля 2022 г.; красным – рассчитанные по первому алгоритму; синим – рассчитанные по второму алгоритму

Таблица 3

Статистические характеристики расчетов

Таблица 4

Величины суммарного слоя таяния

Рассчитанная величина суммарного стока за рассмотренный период по первому алгоритму завышает суммарный сток на 10 %, по второму – на 4 % (табл. 4), что в целом можно считать удовлетворительным результатом в обоих случаях.

Несмотря на то, что рассматриваемые алгоритмы основаны на уравнении теплового баланса, результаты расчета заметно различаются. Было выявлено, что наибольшую погрешность в расчете первой модели вносит турбулентный теплообмен, для определения которого необходимо рассчитывать суточные величины испарения. В случае расчета последнего по формуле Семенова турбулентный теплообмен не зависит от влажности воздуха, что вносит ошибку в расчет. Кроме того, при расчете по первому алгоритму величина встречного излучения атмосферы принимается как константа (табл. 2) и не отражает реально существующую динамику, что также может вносить большую погрешность. Отметим также, что существенную ошибку при расчетах может вносить неточное определение значений суммарной солнечной радиации [5, с. 157]. Также рекомендуется использовать значения альбедо, полученные с помощью специального оборудования в полевых условиях. Особое внимание хотелось бы обратить на коэффициент Dz. Необходимость его применения была выявлена в процессе численных экспериментов.

Все вышеприведенные факторы способны вызывать в той или иной мере погрешности и ошибки расчета. Первый алгоритм явно завышает данные, полученные в результате расчетов, из-за неподходящего уравнения для вычисления суточного испарения и одновременно занижает из-за принятия значения встречного излучения атмосферы как константы. Наиболее интересен тот факт, что в сумме эти параметры дают близкие друг к другу значения, то есть ошибки нивелируют друг друга. Модель П.П. Кузьмина может занижать рассчитанные слои стока из-за недоучета тепла, приносимого с осадками.

Заключение

При тестировании алгоритмов наилучшие результаты показала модель, основанная на уравнении П.П. Кузьмина, коэффициент корреляции для расчетов стока с ледника составил 0,61 при критическом значении 0,46. Вторая модель при учете бо́льшего количества составляющих теплового баланса показала менее точный результат из-за существенных погрешностей в расчете испарения и недоучете изменения величины встречного излучения атмосферы (принималась как константа).

В дальнейшем для расчета слоев стока с ледников Алтая планируется использовать алгоритм, основанный на уравнении П.П. Кузьмина с учетом тепла, приносимого с осадками, и измеренных в полевых условиях значений приходящей радиации и скорости ветра.