Как правило, в процессе гравитационного обогащения в концентрат переходят пустые минералы высокой плотности, в том числе материалы с высокой магнитной восприимчивостью, в первую очередь магнетит и железный скрап. Наличие их в концентратах усложняет процесс получения высококачественных концентратов. А процесс доводки их сложен, энергоемок и требует многоцикловой переработки с последовательным удалением магнитной сепарацией.
Наряду с применением обычных методов магнитной сепарации с использованием традиционных магнитных сепараторов в практике золотодобычи широко применяются магнитогидродинамический, магнитогидростатический методы, магнитно-флокуляционная, магнитно-гравитационная сепарации [1–3], а также магнитная сепарация в импульсных градиентных полях [4].
Вместе с тем проблема поиска новых технологических решений в эффективной переработке и доводке концентратов остается актуальной.
В лаборатории ОПИ разработан способ обогащения в отсадочной машине с магнитной системой. Применение комбинированного воздействия гравитационных и магнитных полей на процесс разделения золота из магнитных материалов при отсадке позволяет совмещать процессы магнитной сепарации и гравитационной доводки шлихов и концентратов в одном аппарате – отсадочной машине с магнитной системой.
Цель исследования – исследование проницаемости тяжелых ценных компонентов через толщу магнитной постели в камерный продукт отсадочной машины в поле действия полюсопеременного магнитного поля и разработка модели вероятности осаждения.
В известных способах извлечения золота с использованием магнитного поля, например на шлюзе с уложенными на донной части постоянными магнитами, достигается концентрация золота по принципу формирования улавливающего магнитно-сфлокулированного коврика (постели). Золото концентрируется на таком коврике, но при нарастании количества материала и минералов с магнитными свойствами становится проблема последующего разделения золота от такого «ковра» [5].
Для решения данной проблемы был предложен способ отсадки в магнитном поле, достигаемый за счет установки постоянных магнитов на отсадочном решете. Однако эксперименты показали, что в этом случае происходило интенсивное накопление (спрессование) магнитных материалов. Образующаяся структура сложно поддается разрыхлению гидродинамическими силами (восходящие и нисходящие циклы отсадки). При усилении параметров отсадочного цикла, амплитуды и частоты, равномерность распределения материала в постели нарушается, образуются зоны пробивания, и процесс разделения расстраивается. Таким образом, определяющим фактором эффективного извлечения золота при отсадке в поле действия магнитного поля является обеспечение разрыхленного состояния постели, но и не менее важным – обеспечение однородности постели по всей площади.
Следовательно, магнитное поле, создаваемое магнитной системой, должно быть динамичным. Наиболее рациональные условия обеспечения разрыхленности и однородности постели достигаются при использовании полюсопеременного магнитного поля [6].
Нами разработан электроимпульсный источник для создания полюсопеременного магнитного поля, позволяющий обеспечить разрыхленное состояние постели. На решето устанавливается ячейка с расположением на специальных держателях постоянных магнитов и электромагнитов (рис. 1).
Рис. 1. Общий вид электромагнитной ячейки и электроимпульсного источника на отсадочной машине МОД-0,2; 1 – электромагнитная ячейка; 2 – электроимпульсный источник; 3 – отсадочная машина МОД-0,2
Благодаря постоянным магнитам в постели поддерживается постоянная концентрация магнитных минералов. При этом в результате непрерывной перемены полюсов источника магнитного поля (электромагнитов) в ячейке образуется подвижная постель, тем самым достигается ее разрыхленное состояние. При этом исключается переуплотнение постели и благодаря обеспечению подвижности и разрыхленности постели под действием пульсирующих циклов отсадки обеспечивается сегрегационное осаждение и проницаемость тяжелых частиц извлекаемых полезных компонентов (золото) через толщу постели в камерный продукт отсадочной машины.
Физико-математическое моделирование
Для моделирования процесса отсадки используется теория броуновской частицы, где решается уравнение типа Фоккера – Планка [7].
На поддержание разрыхленного состояния постели, сформированной из магнитных материалов, вследствие образования сфлокулированных структур, выстраивающихся вдоль линий магнитной индукции, недостаточно использования пульсирующих нисходящих и восходящих потоков воды. При применении постоянного магнитного поля постель отсадочной машины не способна пропускать через себя тяжелые немагнитные частицы. А при применении полюсопеременного магнитного поля магнитные частицы переходят в дополнительное колебательное перемещение (движение) за счет периодического изменения силовых линий примерно на 90° (при сочетании действия постоянного магнитного поля и электромагнитного поля) с частотой, соответствующей частоте периодического изменения полюсов источника магнитного поля. Физическая модель процесса основана на представлении вероятности выхода немагнитных тяжелых частиц из области окружения колеблющихся магнитных частиц, которые совершают колебательные движения с амплитудой примерно равной размеру зерен и с частотой, соответствующей частоте источника переменного магнитного поля. Последние, совершая колебательные движения с определенной частотой и амплитудой, бомбардируют исследуемую частицу. В результате частица совершает марковский процесс, т.е. случайные дискретные перемещения, независящие от предыстории, но под воздействием силы тяжести перемещается вниз. Такой процесс описывается уравнением типа Фоккера – Планка, решение которого представлено в теории движения броуновской частицы [8].
На основании уравнения типа Фоккера – Планка для отсадочного процесса, находящегося в поле действия полюсопеременного магнитного поля, в результате физико-математического моделирования определена формула расчета вероятности прохождения немагнитной частицы с массой m в плотной постели определенной толщины, сформированной частицами с высокой магнитной восприимчивостью (магнитных шлихов) в зависимости от времени:
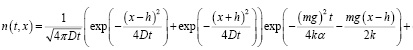
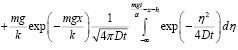, (1)
где х [м] – координаты исследуемой частицы, отсчитываемые от нижней поверхности постели отсадочной машины, h [м] – высота постели, m [кг] – масса частицы, g – [м/с2] ускорение свободного падения, D = k / α [м2/с],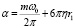 
[кг/с] – коэффициент сопротивления среды, ω0 [1/с] – частота колебаний зерен шлиха, η [кг/м с] – вязкость среды, r1 [м] – радиус исследуемой частицы, k [Дж] – коэффициент градиентной силы, которая пропорциональна энергии бомбардирующих частиц окружающей среды, n(t, x) [1/м] – плотность вероятности.
В модели рассматривается движение частицы меньшего размера (принята шарообразная форма частицы), чем окружающие. Определяется зависимость вероятности выхода данной немагнитной частицы с массой m и с размером r1 из окружения частиц с условными радиусами r0. Моделируется вероятность перемещения тяжелой частицы под воздействием силы тяжести и условий отсадки через толщу постели (высоты h).
Рассматривается поведение частицы в полой области, которая появляется вокруг исследуемой частицы, при колебательных процессах плотноупакованной системы. Полую область можно рассматривать как сферическую поверхность определенного размера l с проемами (рис. 2). Размер полой области зависит от амплитуды колебательных движений системы a, т.е. l = 2r0 + a. С расширением полой области увеличиваются проемы между частицами, где может протиснуться рассматриваемая частица радиуса r1.
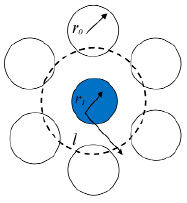
Рис. 2. Область движения исследуемой частицы радиуса r1, r0 – радиус окружающих шаров
Площади этих проемов, через которые может протиснуться частица, зависят от амплитуды колебаний постели, а вероятность прохождения частицы через нее – от размера исследуемой частицы, частоты колебаний постели и площади проемов. Так, просуммировав эти площади и обозначив S, мы можем полую область рассматривать как сферу с проемом, площадь которого пропорциональна квадрату радиуса сферы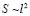 
, т.е.:
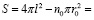
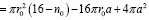, (2)
где n0 – количество частиц ближайшего окружения рассматриваемой частицы при плотной упаковке.
Вероятность того, что частица покинет данную сферу, пропорциональна потоку частиц через эту площадь:
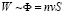, (3)
где n – «концентрация» частиц внутри полой области, которая пропорциональна частоте колебательных движений системы, v – скорость частицы, равная скорости частиц окружающей среды, которая пропорциональна также частоте колебаний среды и ее амплитуде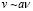 
.
Если исследуемая частица размером меньше, то вероятность увеличивается как отношение площади S к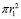 
. Таким образом, для вероятности прохождения частицы через проемы получается следующее выражение:
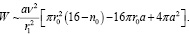(4)
Выражение (4) в уравнение для вероятности (1) входит как множитель к коэффициенту диффузии:
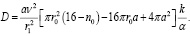(5)
На рис. 3 представлены графики распределения вероятности местонахождения исследуемой частицы в постели отсадочной машины с различными размерами, рассчитанные по формулам (1) и (4). Приводятся зависимости плотности вероятности местонахождения исследуемой частицы по высоте постели отсадочной машины. По вертикали – координаты частицы, по горизонтали – плотности вероятности. Например, через 2 мин после начала движения наиболее вероятное местонахождение исследуемой частицы (максимальное значение красной линии) находилось на высоте 1 м, через десять минут вероятное положение частицы расползается и опускается вниз (синяя пунктирная линия) и т.д. Дальше изображены вероятности через 22, 32, 42 мин. На рис. 3, б, представлены графики вероятностей для частицы меньшего в 1,5 раза размера при тех же условиях. Рисунок наглядно показывает, что, согласно модели, движение частицы меньшего размера происходит быстрее.
Экспериментальные исследования проводились с естественными шлиховыми концентратами месторождения Большой Куранах. Шлиховой материал представлен главным образом магнетитом, рыхлыми гидроокислами железа, гематитом и тяжелыми минералами.
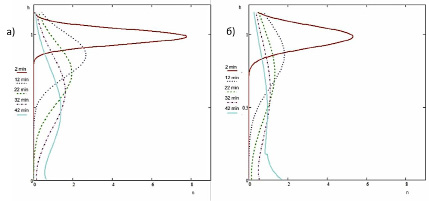
Рис. 3. Относительная вероятность местонахождения частицы в отсадочной машине с различными размерами при одинаковых условиях: a) движение частицы с радиусом r1, б) движение частицы с радиусом r1/1,5, через различные промежутки времени. По вертикали – высота координат частицы, по горизонтали – относительная вероятность
В качестве имитатора золота использовался вольфрам, как наиболее близкий металл по плотности, 19,3 г/см3. Были проведены эксперименты с использованием вольфрама разной крупности: -2,5+1,6 мм, -1,6+1 мм, -1+0 мм по следующей методике: загружается магнитный шлих крупностью -2,5+2 мм в ячейку, после того, как образуется ворсистая постель, включается отсадочная машина и электроимпульсный источник, подается песок (в качестве легкой фракции) с добавлением 10 шт. вольфрама, время проведения экспериментов – 3, 5, 7 мин. Экспериментальными исследованиями на отсадочной машине с электромагнитным источником установлены рациональные значения: частота отсадочного цикла 210 мин-1, высота постели 80 мм, амплитуда 6 мм, длительность импульсов полюсопеременного магнитного поля 0,1 с.
На основе разработанной теоретической модели рассчитана вероятность прохождения исследуемой частицы через толщу постели. На рис. 4 представлен алгоритм расчета вероятности прохождения частицы через постель высотой h. Плотность вероятности в определенный момент времени изображена красной линией. Желтая область есть вероятность проникновения исследуемой частицы через толщу постели. Она определяется интегрированием кривой от нуля до границы слоя как площадь желтой области. При расчетах параметры модели были адаптированы к экспериментальным данным.
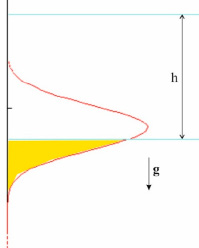
Рис. 4. Вероятность положения исследуемой частицы в постели отсадочной машины в некоторый момент времени. Желтая область – прошедшая через слой часть вероятности
На рис. 5 представлено сравнение расчетной вероятности и результатов экспериментальных данных прохождения вольфрама разной крупности 2,5+1,6 мм, -1,6+1 мм, -1+0 мм через толщу магнитной постели на отсадочной машине с электромагнитным источником по времени.
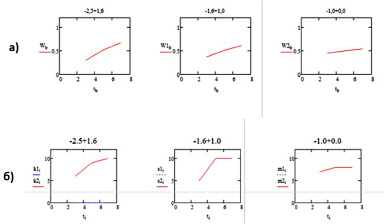
Рис. 5. Сравнение расчетной вероятности и экспериментальных значений проницаемости вольфрама по классам крупности: а) расчетная вероятность; б) экспериментальные данные
Полученная вероятность движения частицы моделирует движение тяжелой частицы вольфрама через постель отсадочной машины, сформированной из магнитных частиц (шлихов) по времени, которая согласуется с полученными экспериментальными данными.
Заключение
Важнейшим фактором процесса эффективного извлечения золота из шлиховых продуктов обогащения с содержанием железного скрапа и минералов с высокой магнитной восприимчивостью в отсадочной машине является постоянная разрыхленность формирующейся естественной постели, поддерживаемая полюсопеременным магнитным полем. Разработана физико-математическая модель на основании уравнения типа Фоккера – Планка по определению вероятности прохождения через толщу постели тяжелых минеральных частиц при условии требуемого состояния разрыхленности.
Апробация модели показывает, что полученные расчеты коррелируются с результатами экспериментов на отсадочной машине с электромагнитной установкой при условиях отсадочного процесса: частоте отсадочного цикла 210 мин-1, высоте постели 80 мм, амплитуде 6 мм и длительности импульсов полюсопеременного магнитного поля с 0,1 с.