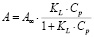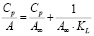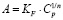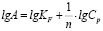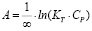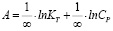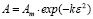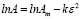Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

В богатой палитре природных ресурсов России представлены обширные запасы опал-кристобалитовых пород. В их числе значительный объем занимают диатомитовые залежи. Диатомиты различных месторождений схожи по химическому составу [1–3]. Это биоморфные тонкозернистые породы пелитоморфной структуры, в минералогическом составе которых преобладает аморфный кремнезем, а также имеются глинистые включения. Общей особенностью породы является наличие пористой структуры.

Химический состав, пористая структура и физические свойства диатомита определяют широкий спектр применения в различных технологиях. Микроэлементный состав породы позволяет использовать его как фильтровальный материал [1, с. 101].

Отмеченные особенности диатомита определяют практическую значимость его использования в развитии технологической культуры в рамках «зеленой повестки». При этом в современных условиях особое значение в природосообразной деятельности имеет водоочистка от экологически опасных для окружающей среды тяжелых металлов [4–6]. Характерным и распространенным загрязнителем природных и сточных вод являются ионы цинка. Цинк мигрирует в гидросферу в результате разрушения горных пород и минералов, недостаточной очистки сточных вод горно-обогатительных комбинатов, гальванических цехов, производств минеральных красок, вискозного волокна и других производств [7]. В этом контексте актуальным направлением исследований является изучение сорбционных характеристик фильтровальных материалов.

Цель исследования – изучение сорбционных свойств диатомита в растворах, содержащих ионы цинка, с возможным использованием данного природного сорбента в технологии обработки промышленных сточных вод.

Материалы и методы исследования

Исследования проводили на природном диатомите Ирбитского месторождения (Свердловская область). Он представляет собой мелкодисперсный пылеватый порошок светло-серого цвета. Химический состав диатомита был установлен с помощью сканирующей электронной микроскопии [4] и представлен в табл. 1. По результатам анализа видно, что основным компонентом природного минерала является диоксид кремния, что объясняет высокую кислотостойкость сорбента.

Сорбционную активность диатомита изучали в статических условиях на модельных растворах сульфата цинка при температурах 298, 318 и 333 К. Для этого 1 г сорбента заливали 50 мл модельного раствора с переменным содержанием ионов цинка. Приготовленные системы выдерживали при заданной температуре до установления сорбционного равновесия. Концентрацию ионов цинка определяли трилонометрическим методом. Количество поглощенных ионов (ммоль/г) рассчитывали по формуле

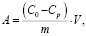ммоль/г ,

где С0 и Ср – исходная и равновесная концентрации ионов цинка в растворе, ммоль/мл; V – объем исходного раствора, мл; m – масса навески сорбента, г.

Для повышения сорбционной активности природного диатомита проводили химическую модификацию минерала растворами соляной кислоты, гидроксида натрия и хлорида натрия методом пропитки в течение одних суток с концентрацией модификаторов 0,2 М.

Для описания процесса сорбции использовали модели Ленгмюра, Фрейндлиха, Тёмкина и Дубинина – Радушкевича. Параметры моделей были определены по результатам статистической обработки эксперимента методом наименьших квадратов (МНК) с использованием онлайн-калькулятора «Math». При этом модельное представление было линеаризовано с помощью стандартных математических преобразований.

Таблица 1

Химический состав диатомита Ирбитского месторождения

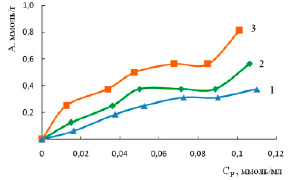
Рис. 1. Изотермы сорбции ионов цинка на природном диатомите при температурах, К: 298 (1), 318 (2), 333 (3)

Результаты исследования и их обсуждение

Любая разработка технологии сорбционной очистки требует изучения закономерностей процесса сорбции. Основные сведения о сорбционной способности диатомита могут быть получены из изотерм сорбции. На рис. 1 представлены изотермы адсорбции ионов цинка диатомитом в природной форме при различных температурах.

Как видно из рис. 1, сорбционная активность диатомита по отношению к ионам цинка с ростом температуры имеет эндотермический характер. Экспериментальные данные позволяют предположить хемосорбционное взаимодействие сорбата и сорбента. Вид полученных изотерм характерен для природных сорбентов [8].

Для количественной оценки закономерностей процесса сорбции ионов цинка на природном диатомите использовали модели сорбционных равновесий, приведенные в табл. 2.

Модель Ленгмюра предполагает наличие определенного числа активных сорбционных центров с одним и тем же сорбционным потенциалом, что способствует образованию монослоя сорбата. В данной модели А∞ – предельная адсорбционная емкость монослоя и KL – постоянная сорбционного равновесия. Модель Фрейндлиха применяют для описания адсорбции на неоднородной поверхности с неравномерным распределением активных адсорбционных центров по величинам энергии адсорбции. В данной модели KF – константа, относящаяся к адсорбционной емкости, 1/n – параметр, характеризующий интенсивность сорбционного процесса. Модель Тёмкина описывает изотерму адсорбции на равномерно неоднородной поверхности адсорбента. В данной модели KT – константа сорбционного равновесия, ∞ – константа, характеризующая теплоту адсорбции.

Представленные модели не дают информации о природе взаимодействия адсорбата и адсорбента. Для этих целей используют модель Дубинина – Радушкевича, которая позволяет установить физический или химический механизм адсорбционного взаимодействия. В даной модели Аm – максимальная сорбционная емкость, k – константа, связанная с энергией адсорбции (Е); ε – потенциал Поляни [9].

Графическую проверку выполнения соответствующих моделей проводили по линеаризованным формам уравнений, что позволяет констатировать выполнение той или иной закономерности без учета констант, входящих в эти уравнения. Графическая интерпретация линеаризованных экспериментальных данных для статистической обработки в модели Фрейндлиха представлена на рис. 2.

В процессе статистической обработки экспериментальных данных были определены:

− параметры уравнения линейной регрессии y = a + bx, линейный коэффициент корреляции с проверкой его значимости;

− теснота связи с помощью показателей корреляции и детерминации, МНК-оценка, статическая надежность регрессионного моделирования с помощью F-критерия Фишера и с помощью t-критерия Стьюдента, доверительный интервал прогноза для уровня значимости 0,05.

Таблица 2

Модели сорбционных равновесий

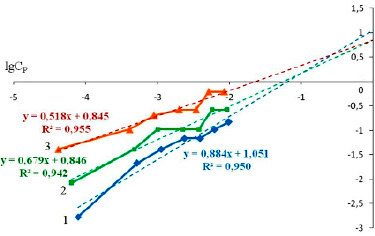
Рис. 2. Изотермы сорбции ионов цинка на диатомите при температурах, К: 298 (1), 318 (2), 333 (3), в линейных координатах (модель Фрейндлиха)

Таблица 3

Результаты математического описания изотермы сорбции при 318 К различными моделями

Что касается МНК-оценки, то проверка наличия предпосылок МНК была выполнена по следующим показателям:

− проверка на наличие автокорреляции остатков по критерию Дарбина – Уотсона;

− проверка нормальности распределения остаточной компоненты по RS-критерию;

− проверка гетероскедастичности и гомоскедастичности с использованием теста Спирмена.

В табл. 3 в качестве примера представлены результаты статистической обработки математического описания изотермы сорбции ионов цинка при 318 К различными моделями.

Выполнена оценка параметров моделей сорбции методом наименьших квадратов. Статистическая значимость уравнений проверена с помощью коэффициентов детерминации и критерия Фишера. Установлено, что в исследуемой системе от 77,39 до 96,81 % общей вариабельности количества поглощенных ионов цинка объясняется изменением равновесной концентрации ионов цинка в растворе (потенциалом Поляни в модели Дубинина – Радушкевича). Также определено, что параметры модели статистически значимы. Наряду с этим в модели Дубинина – Радушкевича не подтверждается значимость коэффициента а.

Однако в данном случае коэффициентом a нельзя пренебречь, что подтверждает оценка статистической значимости уравнения регрессии по F-критерию Фишера, а также адекватность модели по нормальности распределения остаточной компоненты. Представленные оценки уравнений регрессии позволяют использовать их для прогноза. Линейные коэффициенты корреляции изменяются от 0,88 до 0,984, следовательно, связь между количеством поглощенных ионов и равновесной концентрацией ионов цинка весьма высокая и прямая. Также подтверждена значимость линейных коэффициентов корреляции.

Значение ошибки аппроксимации (8,4–12,4 %) говорит об удовлетворительном качестве используемых моделей. Проверка предпосылок МНК подтвердила корректность использования данного метода для построения уравнений регрессии.

В результате статистической обработки экспериментальных данных изотерм сорбции были определены параметры в используемых моделях, табл. 4.

Таблица 4

Параметры сорбции ионов цинка природным диатомитом при различных температурах

Табличные данные показывают, что модель Ленгмюра не подходит для описания адсорбции ионов цинка на диатомите из-за низкого коэффициента детерминации (R2), который повышается с ростом температуры, что, вероятно, связано с перераспределением доли вклада протекаемого вида сорбции (физической, химической либо ионообменной). Увеличение температуры приводит к усилению взаимодействия сорбат – сорбент, что подтверждается возрастанием константы Ленгмюра (КL). По полученным в табл. 4 данным видно, что при описании адсорбционного равновесия ионов цинка на природном сорбенте можно применять уравнения для неоднородной поверхности (модели Фрейндлиха и Тёмкина). Активные адсорбционные центры по этим моделям обладают различными величинами энергии и происходит преимущественное заполнение адсорбционных центров с максимальной энергией. Модель Тёмкина хорошо описывает изучаемый сорбционный процесс, с ростом температуры усиливается взаимодействие между адсорбционными центрами природного диатомита и ионами цинка (КТ возрастает). Но модель Фрейндлиха лучше коррелирует с экспериментальными данными, поскольку для нее коэффициенты детерминации больше, чем в модели Тёмкина. Это указывает на экспоненциальное распределение энергии адсорбционных центров, и эта неоднородность с ростом температуры увеличивается (1/n→0).

По модели адсорбции Дубинина – Радушкевича коэффициенты детерминации достаточно высокие, с ростом температуры свободная энергия адсорбции (Е) возрастает, но всё в пределах физической природы взаимодействия адсорбата и адсорбента до 8 кДж/моль.

Путем сопоставления коэффициентов детерминации для описания сорбции ионов цинка природным диатомитом модели составляют следующие ряды:

298 К: Ленгмюра < Фрейндлиха < Тёмкина < Дубинина – Радушкевича;

318 К: Ленгмюра < Тёмкина < Фрейндлиха < Дубинина – Радушкевича;

333 К: Ленгмюра < Тёмкина < Дубинина – Радушкевича < Фрейндлиха.

По полученным рядам наглядно видно, что повышение температуры способствует протеканию сорбционного процесса на активных центрах с максимальной энергией неоднородной поверхности сорбента (по модели Фрейндлиха).

Природные диатомиты обладают достаточно хорошей сорбционной способностью, однако повысить их сорбционную емкость можно модифицированием поверхностных слоев. Химическая модификация сорбента может быть кислотной, щелочной [5, 6] либо их сочетанием [10], а также распространена солевая обработка поверхности [11]. При этом активация диатомита направлена на улучшение степени дисперсности и пористости сорбента, а также на изменение химической природы поверхности сорбента путем закрепления на активных центрах модифицирующего агента [3, 10]. Результат модифицирования определяется природой и концентрацией модификатора, природой сорбента, а также технологическими параметрами (температурой обработки, временем контактирования с модификатором, промывкой от мешающих ионов и др.).

На рис. 3 приведены изотермы сорбции ионов цинка на диатомите при химических модификациях. Из рисунка видно, что предварительная пропитка сорбента раствором соляной кислоты не приводит к увеличению сорбции. Эффект снижения поглощения ионов тяжелых металлов при кислотной активации диатомита также отмечен в работах [5, 6].

На начальном участке изотерм можно отметить эффект интенсификации процесса для щелочной и солевой форм сорбента. В целом величина сорбции диатомита, обработанного хлоридом натрия, возрастает по сравнению с природной формой, а при обработке щелочью снижается с ростом концентрации.

Найденные параметры сорбции ионов цинка на модифицированном диатомите позволяют сделать вывод, что при обработке сорбента модификаторами происходит изменение его поверхности в сторону большей неоднородности (1/n уменьшается) по сравнению с природной формой (табл. 5). Модель Тёмкина не описывает сорбцию на модифицированном диатомите (низкие значения коэффициентов детерминации). Из данных табл. 4 и 5 видно, что сорбционный процесс протекает с одинаковой интенсивностью, если его проводить при 333 К либо на солевой форме сорбента. Для разработки технологии сорбционной очистки предпочтительнее использование солевой формы диатомита, так как это менее энергозатратно.

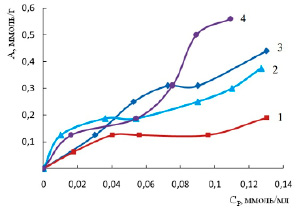
Рис. 3. Изотермы сорбции ионов цинка на диатомите при температуре 298 К, обработка сорбента: кислотная (1), щелочная (2), природная форма (3), солевая (4)

Таблица 5

Параметры сорбции ионов цинка природным и модифицированным диатомитом при 298 К

Заключение

Проведены исследования по изучению сорбционных свойств природного и модифицированного диатомита в водных растворах, содержащих ионы цинка. Поглощающая способность природной формы диатомита увеличивается с ростом температуры. Также повышение сорбционной емкости диатомита отмечено при солевой обработке сорбента. Поэтому изучаемый природный сорбент (диатомит) можно использовать в обработке промышленных сточных вод.