Введение
Часто бывает ситуация, когда на месторождениях полиметаллических руд при отборе проб преимущество отдается наиболее ценному компоненту. Например, на месторождении основным компонентом является золото, а попутным – серебро, и на определение золота в лабораторию отдаются абсолютно все пробы, а на определение серебра – лишь некоторая часть. Как итог – в базе данных имеем очень много проб с содержанием золота и лишь небольшую часть – с содержанием серебра. Встает вопрос: как корректно произвести оценку содержаний серебра на всем месторождении при малом количестве проб? В таком случае рекомендуется использовать кокригинг. Кокригинг – это метод интерполяции, который используется при наличии двух или более сильно коррелированных между собой компонентов, когда количество проб одного компонента значительно меньше, чем количество проб остальных компонентов [1]. При кокригинге оцениваемый компонент оценивается на основе его собственных измерений и данных по другим, коррелирующим компонентам. По сути, кокригинг представляет собой комбинацию кригинга и регрессии. Теоретически кокригинг не имеет ограничений на число компонентов, и добавление новой информации должно вести к улучшению оценки. На практике это не совсем так. В случае K переменных для кокригинга требуется К(К+1)/2 моделей вариограмм. Проверка всех гипотез для такого количества данных и последующее совместное моделирование становятся достаточно трудоемкими. Кроме того, оценка экспериментальных вариограмм, кросс-вариограмм и их моделирование на практике выполняются с некоторой ошибкой. Большое количество моделей вариограмм может настолько усложнить вычисление окончательной оценки, что результат даже ухудшится. Поэтому важно подбирать правильное количество компонентов и выбирать те, использование которых действительно приводит к улучшению оценки.
Чем выше корреляция между переменными, тем более эффективным будет кокригинг. Если корреляции между компонентами не наблюдается, то использовать кокригинг бессмысленно. Для достаточно большого числа точек опробования (несколько сотен и выше) коэффициенты корреляции, превышающие по модулю 0,5, оказываются значимыми, и, соответственно, применение кокригинга обосновано.
Исследование направлено на демонстрацию работы метода кокригинга на простом примере с целью популяризации данного метода у отечественных специалистов. В статье представлен пошаговый алгоритм работы кокригинга на примере нескольких проб, демонстрирующий его применение и эффективность в оценке содержаний. Следует отметить, что приведенный в статье пример, с квадратной сетью из 9 точек и расчетом ориентированной полувариограммы вдоль горизонтальных направлений, очень упрощенный и носит исключительно учебный характер.
Материалы и методы исследования
Вариограммы
Предположим, что необходимо оценить содержание золота в точке x. В пробе 1 имеется содержание только золота, в пробе 2 имеется содержание только серебра, а в пробе 3 – и золота, и серебра. Предположим, что предварительно по достаточно большому полю наблюдения и числу проб установлена значимая корреляционная зависимость между Au и Ag и присутствует желание использовать все 3 пробы для оценки золота в точке x.
Для этого, в первую очередь, необходимо подобрать модель вариограмм для каждого компонента. Назовем данные вариограммы простыми вариограммами. Формула для расчета простых вариограмм для рассматриваемого примера будет иметь вид:
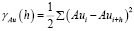
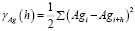
где i – номер пробы, а i+h – номер пробы, удаленной от предыдущей пробы на расстояние h.
Рисунок 1 иллюстрирует пример расчета значений простых вариограмм для двух компонентов в направлении с запада на восток с расстоянием между скважинами 5 метров.
Далее необходимо оценить пространственную связь между компонентами. Для этого рассчитываются перекрестные вариограммы, которые фиксируют корреляцию между компонентами [2]. По сути, перекрестные вариограммы являются произведением двух простых вариограмм.
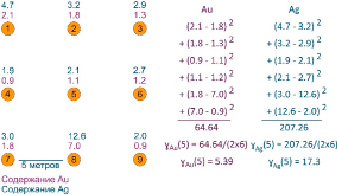
Рис. 1. Пример расчета значений простых вариограмм

Рис. 2. Пример расчета значений перекрестной вариограммы
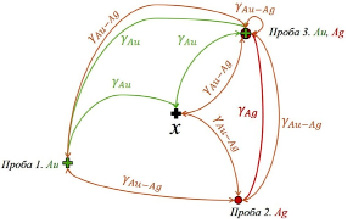
Рис. 3. Использование моделей вариограмм в зависимости от расстояния
Если принять, что в абсолютно каждой пробе измерены значения двух компонентов, то значение перекрестной вариограммы при расстоянии между пробами, равном h, рассчитывается как произведение значений вариограмм для всех проб одного компонента, находящихся друг от друга на расстоянии h, и значений вариограмм всех проб другого компонента, разделенных тем же расстоянием h [3]. Если записать предыдущее предложение формулой, то получим:
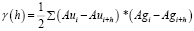
Рисунок 2 иллюстрирует пример расчета значений перекрестной вариограммы для двух компонентов в направлении с запада на восток с расстоянием между скважинами 5 метров.
Модели прямых и перекрестных вариограмм будут использоваться в качестве «таблицы подстановок», по которой определяются значения вариограммы, соответствующие определенному расстоянию [4, с. 151–211] (рис. 3).
По модели простой вариограммы по золоту будут рассчитываться значения вариограммы для расстояний между «пробой 1 и пробой 3», «пробой 1 и точкой x», «пробой 3 и точкой x». По модели простой вариограммы по серебру будет рассчитываться значение вариограммы только для расстояния между «пробой 2 и пробой 3», поскольку в пробе 1 нет серебра. По модели перекрестной вариограммы «золото – серебро» будут рассчитываться значения вариограммы для расстояний между «пробой 1 и пробой 2», «пробой 1 и пробой 3», «пробой 2 и пробой 3», «пробой 2 и пробой 2» (вариограмма на минимально возможном близком расстоянии), «пробой 2 и точкой x», «пробой 3 и точкой x».
Модели простых и перекрестных вариограмм необходимо подбирать в сочетании друг с другом. Ниже описаны основные правила подбора моделей вариограмм, которых рекомендуется придерживаться.
• Рекомендуется использовать как можно меньшее количество структур в моделях простых вариограмм, чтобы было проще впоследствии подобрать модели перекрестных вариограмм.
• Модели перекрестных вариограмм должны содержать такое же количество структур, как и модели прямых вариограмм.
• Зона влияния (range) определяется по простой вариограмме оцениваемого компонента и является неизменной основой для всех остальных моделей, как простых, так и перекрестных вариограмм.
• Эффект самородка (nugget) и пороги (sill) могут быть различны для всех моделей простых и перекрестных вариограмм.
• По возможности моделируйте простые вариограммы с одинаковой ориентацией для всех компонентов. Если разница в ориентации менее 10º, принимайте среднее значение или наиболее сильный тренд.
Оценка содержаний
Формула оценки ординарного кригинга имеет следующий вид:
Содержание в оцениваемой точке = ∑ (содержание в пробе × вес пробы)
Оценка кокригинга представляет собой линейную комбинацию оцениваемого компонента и коррелированных с ним дополнительных компонентов. Формула оценки кокригинга для двух компонентов имеет следующий вид:
Содержание в оцениваемой точке = ∑ (содержание в пробе (1 компонент) × вес пробы) + + ∑ (содержание в пробе (2 компонент) × вес пробы)
В кригинге за несмещенность оценки отвечало условие, что сумма весов всех проб должна быть равна единице. В кокригинге за несмещенность оценки отвечает условие, что сумма весов всех проб оцениваемого компонента должна быть равна единице, в то время как сумма весов всех проб дополнительных компонентов должна быть равна нулю.
Перепишем это в виде системы уравнений для трех проб из рассматриваемого примера:
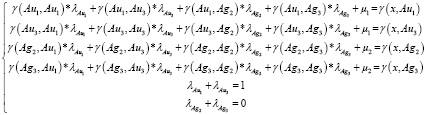
где Au – основной оцениваемый компонент, Ag – дополнительный оцениваемый компонент, γ(Au1, Au2) – значение вариограммы между точками опробования основного оцениваемого компонента, определяющееся по модели простой вариограммы, γ(Ag1, Ag2) – значение вариограммы между точками опробования дополнительного оцениваемого компонента, определяющееся по модели простой вариограммы, γ(Au1, Ag2) – значение вариограммы между точками опробования основного оцениваемого и дополнительного оцениваемого компонента, определяющееся по модели перекрестной вариограммы, λ – вес проб, μ1, μ2 – множители Лагранжа, γ(x, Au1) – значение вариограммы между оцениваемой точкой и пробой.
Один из способов решения данной системы уравнений, который используют большинство ПО, – матричный метод.

Рассчитанные веса используются в дальнейшем для нахождения содержания в оцениваемой точке [5] (рис. 4).
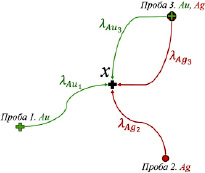
Рис. 4. Использование соответствующих весов проб при оценке
После интерполяции содержаний рекомендуется для каждого выделенного домена определить коэффициенты корреляции между оцениваемым и дополнительными компонентами в блочной модели и сравнить их с исходными коэффициентами корреляции по данным опробования [6]. Они должны быть схожи. Сильное различие говорит о возможно допущенных ошибках в процессе оценки [7, 8].
Результаты исследования и их обсуждение
В качестве упрощенного примера, для простоты расчетов, рассмотрим оценку одной ячейки блочной модели с дискретизацией 1х1x1 по направлениям X, Y, Z (рис. 5).
1. Производим поиск ближайших проб с использованием эллипсоида поиска. Эллипсоид поиска всегда размещается в центре материнской ячейки. В дальнейшем используются только те пробы, которые попали в эллипсоид поиска.
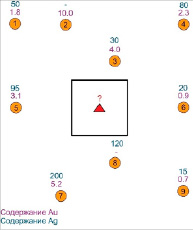
Рис. 5. Исходные данные для оценки
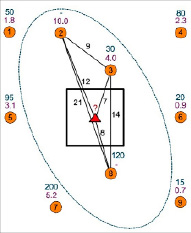
Рис. 6. Измеряется расстояние между всеми пробами и расстояние между каждой пробой и центром блока
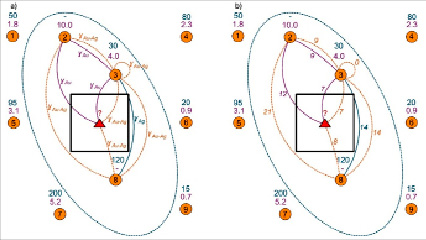
Рис. 7. Использование моделей вариограмм: a) используемые модели; b) используемые расстояния
2. Измеряем расстояние между всеми пробами и расстояние между каждой пробой и всеми точками дискретизации (рис. 6). В рассматриваемом примере это расстояние до центра блока.
3. На основании заранее построенных простых моделей вариограмм для Au и Ag и перекрестной модели вариограммы Au-Ag вычисляются значения вариограмм для каждого из расстояний. По сути, модели вариограмм в данном случае выступают в роли «таблицы подстановок», по которой определяется значение вариограммы, соответствующее определенному расстоянию (рис. 7, 8). По модели простой вариограммы по золоту будут рассчитываться значения вариограммы для расстояний между «пробой 2 и пробой 3», «пробой 2 и оцениваемой точкой», «пробой 3 и оцениваемой точкой». По модели простой вариограммы по серебру будет рассчитываться значение вариограммы только для расстояния между «пробой 3 и пробой 8», поскольку в пробе 2 нет серебра. По модели перекрестной вариограммы «золото – серебро» будут рассчитываться значения вариограммы для расстояний между «пробой 2 и пробой 3», «пробой 2 и пробой 8», «пробой 3 и пробой 8», «пробой 3 и пробой 3» (вариограмма на минимально возможном близком расстоянии), «пробой 3 и оцениваемой точкой», «пробой 8 и оцениваемой точкой».
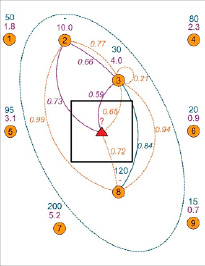
Рис. 8. Значения вариограмм для каждого из расстояний (см. цифры возле линий)
4. Значения вариограмм используются в системе уравнений кокригинга для определения весов проб. В рассматриваемом примере система уравнений будет иметь следующий вид:
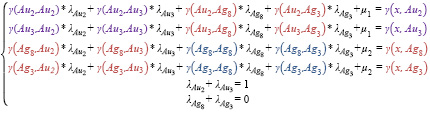
Первые четыре уравнения (по одному на каждое известное значение в пробах) в данной системе отвечают за второй принцип кригинга – наименьшую разницу между истинными и оцененными содержаниями. Последние два уравнения отвечают за первый принцип кригинга – несмещенность оценки. Поскольку нет возможности заранее знать истинные содержание в оцениваемой точке, в уравнении участвуют не содержания, а значения вариограмм [9].
После подстановки вычисленных значений вариограмм система уравнений будет иметь вид:
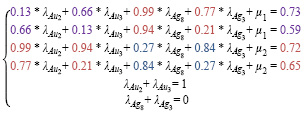
5. В результате решения уравнения рассчитываются следующие весовые коэффициенты:
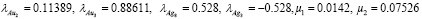
Множители Лагранжа в дальнейшей оценке не участвуют [10].
6. Подставляем весовые коэффициенты и содержания проб в основное уравнение кокригинга:
Содержание Ag в оцениваемой точке = 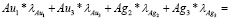
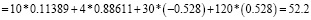
Заключение
В данной статье был представлен метод кокригинга как эффективный инструмент для оценки содержаний. На примере нескольких проб был продемонстрирован пошаговый алгоритм работы кокригинга, позволяющий учесть пространственную корреляцию. Этот метод позволяет улучшить точность прогнозирования из-за использования большего количества исходных данных, что делает его ценным инструментом для геологических исследований и практических применений в горнодобывающей промышленности.



