Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Введение

Удаление различного рода загрязнений из природных и сточных вод является одной из приоритетных проблем XXI века. Тяжелые металлы (ТМ) при повышенной концентрации оказывают токсическое воздействие на все живые организмы [1, с. 16]. Во всех водных объектах Тюменской области присутствуют ионы железа, марганца и меди, согласно мониторингу [2]. Марганец в водных объектах может находиться в разных степенях окисления: Mn2+, Mn3+, Mn4+. Для удаления тяжелых металлов из водной среды перспективным методом является сорбционная технология [3–5]. В качестве сорбентов используют различные материалы, обладающие обменной емкостью [6]. Уральский регион богат глинистыми минералами, способными проявлять сорбционную активность.

Цель исследования – оценка сорбционной активности монтмориллонитовой глины по отношению к ионам ТМ: Fe3+, Mn2+, Cu2+ и Pb2+ с дальнейшим применением исследуемого сорбента для водоочистки.

Материалы и методы исследования

В экспериментах использовалась природная монтмориллонитовая глина. На рисунке 1 представлен химический состав монтмориллонита, полученный рентгеноструктурным анализом (РСА) с применением сканирующего растрового микроскопа JEOLJSM 6510 LV (Япония).

Исследование сорбционных свойств природной монтмориллонитовой глины по отношению к ионам Cu2+, Mn2+, Pb2+, Fe3+ проводились на модельных растворах с концентрациями от 0,01 до 0,2 ммоль/мл. Растворы готовились путем растворения реактивов 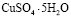, , 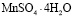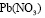и 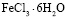в дистиллированной воде. Процесс адсорбции исследуемых ионов металлов проводился статическим способом при температурах 25, 45 и 600С до установления равновесного состояния. При проведении эксперимента во всех случаях объем раствора составлял 50 мл, в который добавляли 1 г монтмориллонита. После установления равновесия определялась остаточная концентрация ионов металлов комплексонометрическим титрованием [7, с. 229, c. 233, c.251, c. 293].

Используя значения концентраций ионов металлов до и после сорбции, рассчитывали сорбционную емкость монтмориллонита по формуле:

,

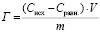где Г – обменная емкость, ммоль/г; Сисх – начальная концентрация ионов металлов, ммоль/мл; Сравн. – равновесное значение концентрации ионов металлов, ммоль/мл; V – объем исходного раствора, мл; m – масса сорбента, г.

По полученным значениям строили изотермы адсорбции, которые обрабатывали моделями Ленгмюра и Фрейндлиха.

Результаты исследования и их обсуждение

Сорбционные свойства монтмориллонитовой глины при сорбции ионов меди, марганца, свинца и железа определяли с помощью изотерм. По полученным экспериментальным данным рассчитывали величину адсорбции Г исследованных ионов с разной исходной концентрацией. На рисунке 2 представлены изотермы сорбции исследуемых катионов металлов на природной глине с содержанием монтмориллонита.

Полученные изотермы по классификации БЭТ для меди, марганца и свинца напоминают изотерму I типа, которая характеризует мономолекулярную адсорбцию, для железа – IV-a типа, характеризующую образование нескольких слоев.

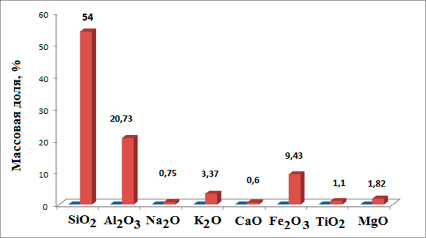
Рис. 1. Химический состав природной монтмориллонитовой глины

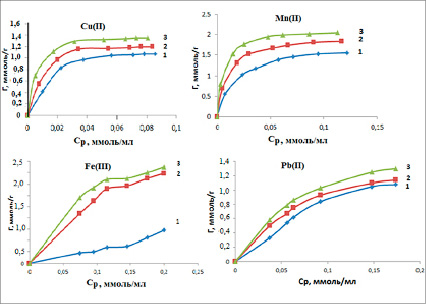
Рис. 2. Изотермы сорбции катионов Cu2+, Mn2+, Pb2+, Fe3+ на природной глине с содержанием монтмориллонита при Т, К: 298 (1), 318 (2), 333 (3).

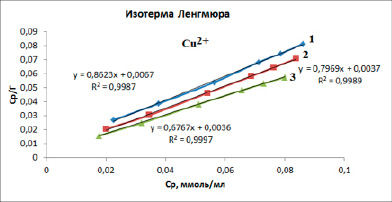
Рис. 3. Изотермы сорбции ионов меди (II) представленные в линейных координатах уравнения Ленгмюра

Наличие выпуклой части изотерм у меди, марганца и свинца обычно связывают с тем, что в сорбенте присутствуют микро- и макропоры. У изотермы железа при Т = 298К отсутствует выпуклый участок – это означает, что адсорбция за счет микропор почти не происходит. Для получения количественных характеристик процесса сорбции экспериментальные данные обрабатывали с использованием уравнения изотермы Ленгмюра (рис. 3) в линейной форме:

,

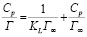где Cp – равновесная концентрация, KL – константа уравнения Ленгмюра, Г∞ – величина предельной сорбции;

и уравнения изотермы Фрейндлиха (рис. 4):

Г = KF ∙ C1/n

где Г – количество адсорбированного иона, ммоль/г, KF и n – константы Фрейндлиха.

Показатель степени n и коэффициент пропорциональности KF в уравнении Фрейндлиха определяли экспериментально. Для этого использовали логарифмические значения в координатах (lgГ)-(lgCp) и строили линейные изотермы. Используя линейное уравнение Ленгмюра, находили значения Г∞ и KL. В таблице 1 представлены результаты расчета констант по уравнению Ленгмюра и в таблице 2 – параметры уравнения Фрейндлиха.

Предельную величину адсорбции Г∞ определяли по графической линейной зависимости по отрезку прямой, отсекаемой на оси ординат. Константу сорбционного равновесия KL определяли по тангенсу угла наклона прямой.

Сорбируемость уменьшается с увеличением радиусов сорбируемых ионов. По значениям величин сорбируемости исследуемые двухзарядные ионы можно расположить в следующий ряд: Mn2+ > Cu2+ > Pb2+.

Известно [8], что изменение температуры оказывает существенное влияние на величину сорбируемости. При увеличении температуры величина сорбции у всех катионов металлов возрастает.

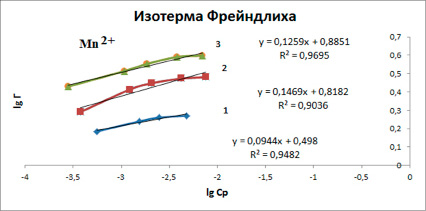
Рис. 4. Изотермы сорбции ионов марганца (II) представленные в линейных координатах уравнения

Таблица 1

Значения предельной величины сорбции Г∞ и константы сорбционного равновесия KL

Таблица 2

Сорбционные константы уравнения Фрейндлиха

Таблица 3

Термодинамические параметры исследуемых ионов металлов

Сравнивая изотермы сорбции катионов Cu2+, Mn2+, Pb2+, Fe3+ при разных температурах получаем следующие закономерности:

Т = 298К Mn2+ > Cu2+ > Fe3+ > Pb2+

Т = 318К Mn2+ > Cu2+ > Fe3+ > Pb2+

Т = 333К Mn2+ > Cu2+ > Pb2+ > Fe3+

Исследование влияния температуры на величину сорбции позволило рассчитать термодинамические параметры. Для расчета свободной энергии Гиббса использовали константу сорбционного равновесия KL:

ΔG = –RTlnKL

Энтальпию ΔH0 рассчитывали, используя уравнения изостеры. Метод расчета теплоты сорбции основан на применении уравнения Клаузиса–Клапейрона:

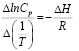, при Г = const

где Cp – равновесная концентрация, ммоль/мл; Т – температура, К; ΔH – изостерическая дифференциальная теплота сорбции, Дж/моль; R – универсальная газовая постоянная, Дж/моль·К.

По рассчитанным значениям ΔG и ΔH определяли значения энтропии по уравнению:

ΔG = ΔH – TΔS

Полученные расчетные данные по термодинамическим параметрам представлены в таблице 3.

Отрицательные значения свободной энергии Гиббса (табл. 3) показывают, что процесс сорбции на поверхности сорбента протекает самопроизвольно. Уменьшение ΔG0 с повышением температуры показывает благоприятное протекание сорбции.

Полученные результаты изотерм сорбции исследованных ионов металлов показывают, что величина ΔH имеет отрицательные значения. Это характеризует протекание сорбции как экзотермического процесса. Монтмориллонит относится к коллоидным слоистым сорбентам. При сорбции происходит изменение структуры сорбента, связанное с разрыхлением поверхностного слоя. В порах сорбента происходит разупорядоченность диполей воды при взаимодействии ионов металлов с активными центрами поверхности. Известно, что природный монтмориллонит имеет подвижную кристаллическую структуру, при увеличении содержания воды расстояние между слоями увеличивается. Это подтверждается и значениями величин энтропии ΔS > 0.

Заключение

Сорбционная способность монтмориллонитовой глины описана моделями Ленгмюра и Фрейндлиха. Определены константы этих уравнений и рассчитаны термодинамические функции сорбционного процесса. Вычисленные термодинамические функции показывают, что процесс сорбции на поверхности монтмориллонитовой глины протекает самопроизвольно. Таким образом, на основании полученных данных по сорбции исследованных ионов установлена возможность использования монтмориллонитовой глины в целях извлечения катионов тяжелых металлов из водных сред.