Введение
При решении широкого круга задач, связанных как с использованием и охраной поверхностных водотоков, так и с минимизацией вредного влияния вод, требуется оценка их транспортирующей способности по отношению как к взвешенным, так и влекомым наносам. В настоящее время прилагаются значительные усилия в исследовании этого вопроса, предлагается значительное количество различных аналитических расчетных соотношений. В то же время в монографии 1990 г. [1]. К.В. Гришанин писал: «Сегодня при применении формул расхода влекомых наносов к естественным потокам приходится встречаться с ошибками, исчисляемыми десятками, а иногда и сотнями процентов». Более того, в настоящее время все больше появляется работ, в которых авторы утверждают, что расчетные соотношения, полученные и отработанные на отдельных реках, тем более на экспериментальных лотках, очень трудно переносятся на другие водотоки, дают при таком переносе неприемлемо высокие погрешности [2–4] и др. В связи с этим стали появляться технологии, не включающие в себя такой, казалось бы, определяющий параметр, как размер транспортируемых частиц d [4].
В то же время при построении большинства расчетных соотношений, как правило, принимается, что исходные определяющие параметры задаются с достаточно высокой надежностью, погрешность их задания меньше, чем погрешность определения расчетных значений. К сожалению, данное условие нередко не выполняется, и исходные параметры задаются со значительной погрешностью. Состав транспортируемых частиц также характеризуется весьма существенной неравномерностью. Данные факторы могут очень существенно влиять на точность, надежность предлагаемых расчетных соотношений.
Материалы и методы исследования
При решении очень широкого круга гидрологических и водохозяйственных задач очень часто возникает задача оценки рассматриваемого параметра x(t) по его ограниченной выборке. При решении практических задач, как правило, в первом приближении принимается, что x(t) описывается нормальным распределением, а сами оценки являются робастными. В этом случае наилучшей оценкой определяющего параметра является среднее арифметическое значение, имеющее при данном объеме выборки минимальную погрешность. Однако в очень многих задачах x(t) входит в знаменатель расчетных соотношений, то есть 1/x(t). В то же время хорошо известно, что
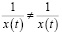, (1)
при этом величина 1/x(t) описывается обратным нормальным распределением [5, 6], для которого не существует первого, второго и более высоких моментов. В данной работе в качестве такого параметра рассматривается размер транспортируемых наносов d. При эйлеровом подходе в любой фиксируемой точке потока изменение размеров транспортируемых наносов будет представлять собой случайный процесс с определенным статистическим описанием. В то же время сами размеры частиц являются определяющим параметром, характеризующим транспортирующую способность водотока.
Аналитические расчетные зависимости являются основным рабочим инструментом в большинстве прикладных, инженерных областей знаний. От корректности данных соотношений зависят все последующие управленческие решения. При этом принципиальное значение приобретает оценка погрешностей рассматриваемой расчетной зависимости, исходя из погрешностей задания исходных параметров.
При этом, если расчетный показатель P, определяемый через N непосредственно измеряемых параметров, то есть P = f(X1, …, XN), а погрешности их определения характеризуются нормальным распределением, то дисперсия оцениваемого показателя будет составлять
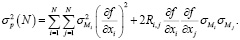(2)
Так как
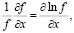(3)
то относительная погрешность оценки будет, соответственно,
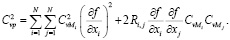(4)
При этом расчетные соотношения (3) и (4) являются неэффективными при σ2p ≥ σ2пр, где σ2р – приемлемая дисперсия для принятия управленческих решений, σ2пр – погрешность рассматриваемой зависимости. При этом возникает задача найти такое соотношение определяющих параметров, чтобы σ2р было бы минимально и удовлетворяло требованию
σ2p < σ2пр. (5)
Поэтому в первую очередь необходима оптимизация выбора определяющих параметров.
Как следует из соотношения (2), для уменьшения дисперсии оцениваемого параметра в расчетных соотношениях должны иметь место статистически независимые параметры. В установившихся прямолинейных водотоках основные морфометрические и динамические параметры потока тесно связаны, что приводит к существенному снижению количества определяющих параметров. Так, наиболее известное соотношение для оценки концентрации взвешенных наносов, г/м3 [7], имеет вид
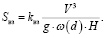(6)
При использовании соотношения Шези для оценки средней скорости потока V и уравнения Штриклера – Маннинга для параметризации коэффициента Шези, а для гидравлической крупности частиц – квадратичного закона сопротивления имеем
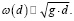(7)
При данных допущениях расчетное соотношение (6) существенно преобразуется и принимает следующий вид
Sвз ~ А / d, где A = kвз1 ∙ H ∙ I 3/2, (8)
где I – уклон водной поверхности, б/р; kвз1 – параметр, г/м3.
При этом уклон водной поверхности является значительно более инерционным показателем динамики потока в отличие от значений локальных скоростей потока. В большинстве расчетных соотношений для оценки расхода влекомых наносов также используют в качестве определяющих параметров скорость и глубину потока, а также размеры транспортируемых частиц [3, 4, 8]. Современные обзоры расчетных соотношений по оценке влекомых наносов даются в работах [9, 10].
Следует заметить, что, вне зависимости от конкретной рассматриваемой модели переноса, интенсивность транспорта частиц должна определяться двумя группами факторов – гидравлических, определяемых динамикой потока, и дисперсионным составом частиц. Соответственно, дисперсия расчетных соотношений также будет определяться особенностями задания этих параметров.
В связи с этим возникает принципиальный вопрос, что является определяющим фактором в формировании повышенной дисперсии при оценке потока наносов? Если перемещение, транспорт наносов определяется из соотношений действующих на частицу силы тяжести и подъемной динамической силы, то зависимость расхода наносов от размера транспортируемых частиц должна иметь в первом приближении следующий вид
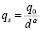, (9)
при этом 1 ≤ α ≤ 2. В достаточно общем случае гидравлическая крупность частиц представляет собой скейлинг от размера частиц
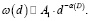(10)
В зависимости от режима осаждения частиц определяемого числом Бонителли D возможен как квадратичный режим турбулентного осаждения α(D) = 1/2 (при D >> 1), так и ламинарного осаждения α(D) = 2 (при D << 1). Таким образом, определяющий параметр для транспорта наносов – размер частиц – входит в знаменатель расчетных соотношений, и при этом размер частиц наносов представляют собой случайную величину, распределение которой существенно отличается от нормального. При этом наличие случайного параметра в знаменателе расчетных соотношений принципиально влияет на характер статистических функций распределения: Sтр(d), qвз(d), qвлк.
Для описания функций распределения скорости осаждения частиц, описываемых соотношением (10), следует воспользоваться соотношением для нелинейного преобразования случайного процесса [5], функция распределения будет описываться как
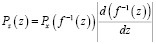, (11)
где f(z) – нелинейная функция преобразования случайного процесса z.
Соответственно, учитывая (8), (9), для статистической функции распределения Sтр(d) будем иметь
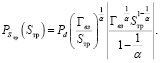(12)
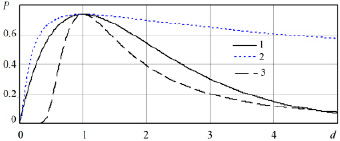
Рис. 1. Сопоставление функции плотности распределения при различных значениях α (1 – P(x) при α = –1; 2 – P2(x) при α = 0.5; 3 – P3(x) при α = –2)
Нелинейное преобразование с переходом аргумента в знаменатель очень существенно изменяет поведение статических функций распределения в области значительных отклонений от средних значений (рис. 1).
Как видно из рис. 1, при α < 0 значительно повышается вероятность наблюдения экстремальных значений, что принципиально меняет характер оценки статистических параметров. При этом значения плотности распределения характеризуются очень медленным снижением вероятностей при d → ∞. Эти распределения в математической статистике получили наименования распределения c «тяжелыми хвостами». Наличие данных «тяжелых хвостов» принципиально влияет на оценку статистических параметров рассматриваемых распределений.
Результаты исследования и их обсуждение
Базовым положением при оценке статистических параметров является априорное допущение их состоятельности, то есть σxср→0 при N → ∞, где σxср – средняя квадратичная погрешность оцениваемого параметра, N – объем рассматриваемой выборки. Выполнимость данной гипотезы относительно первых статистических моментов не вызывает каких–либо сомнений при использования традиционных для гидрологии распределений: нормального, гамма-распределения, логнормального и т.д. Однако в ряде случаев, когда статистические функции были получены в результате нелинейного преобразования данных распределений, ситуация усложняется, интенсивность снижения Р(S) при увеличении S существенно снижается и распределения приобретают свойства распределения с «тяжелыми хвостами».
Так как d в расчетных соотношениях (8, 9) является случайной величиной, то появляется задача оценки среднеквадратичной погрешности σSтр следующей величины:
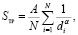(13)
где N – количество выделяемых фракций.
В настоящее время в стохастической гидрологии достаточно хорошо отработана технология моделирования случайных процессов по схеме Монте-Карло [11]. Пример оценки среднеквадратичной погрешности Sтр для среднего и медианы для логнормального распределения представлен на рис. 2.
Как следует из рис. 2, величина σx очень существенно зависит в первую очередь от однородности размеров частиц в исходных выборках. При коэффициенте вариации Сv < 1 рассматриваемые среднеарифметические оценки Sтр, как показали результаты статистического моделирования при N~100 000, вполне состоятельны и эффективны, а σx ~ 0.
В то же время при Сv > 1–1,5 эти оценки являются неустойчивыми. Таким образом, при Сv > 1–1,5 они практически не зависят от характера распределения размера частиц, среднеарифметические оценки становятся несостоятельными и неэффективными, поэтому они не могут быть использованы при оценке транспорта наносов. Установленная неэффективность среднеарифметических значений при Сv > 1–1,5 наглядно объясняет, почему расчетные схемы, отработанные на лотках с достаточно однородными размерами транспортируемых частиц, оказываются в ряде случаев совершенно неэффективными в естественных водотоках с широким диапазоном размеров транспортируемых наносов.
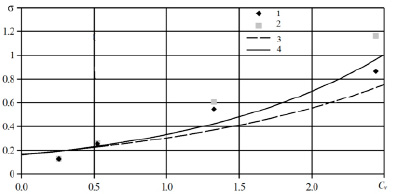
Рис. 2. Зависимость среднеквадратичной относительной погрешности (σx ) средних значений S и медианы (σM ) при S = 1/d1/2 от коэффициента вариации крупности частиц Cv для логнормального распределения d (1 – σx ; 2 – σM ; 3 – аппроксимация σx = f(Cv ); 4 – аппроксимация σМ = f(Cv ))
В настоящее время выполнено большое количество исследований по оценке параметров распределений с «тяжелыми хвостами» [12, 13] и др., для которых не существует не только вторых статистических моментов, но и первых. В простейшем случае предлагается использование в качестве характерных значений не средних арифметических значений, а медианы. Для ухода от «тяжелых хвостов», как правило, используется нелинейное преобразование исходной выборки с использованием некоторых монотонных возрастающих, взаимно-однозначных функций [13].
Выводы
1. Большинство расчетных соотношений по оценке транспорта наносов включает в качестве определяющего параметра размер транспортируемых частиц наносов. При этом, исходя из физики рассматриваемых процессов, они входят в знаменатель этих расчетных зависимостей. В то же время само распределение крупности этих частиц характеризуется существенной изменчивостью. В этом случае суммарные потоки наносов всех фракций будут иметь статистические распределения с очень «тяжелыми хвостами», для оценки которых использование параметрических оценок совершенно неэффективно.
2. Неэффективность использования параметрических оценок для оценки потоков наносов объясняет ситуацию, когда многочисленные расчетные соотношения, полученные на модельных лотках, каналах при переносе на естественные водотоки теряют свою эффективность. Более того, расчетные зависимости, полученные для одного естественного водотока, очень сложно переносятся на другой.
3. Для повышения эффективности расчетных зависимостей для оценки транспортирующей способности русловых потоков необходимо использовать более адекватные, более корректные оценки характерных размеров транспортируемых частиц.