Введение
Динамика параметров рудничной атмосферы и определяющие ее состав сопутствующие явления в значительной степени определяют оптимальный режим проветривания и сохранности горных выработок, соответствие рудничной атмосферы санитарным нормам, а также другие условия, обеспечивающие безопасность эксплуатации и проведения горных работ [1, с. 35; 2]. В условиях криолитозоны учет влияния паров влаги в рудничном воздухе приводит к необходимости рассмотрения их фазовых превращений. Этот момент существенно усложняет задачу конвективного теплопереноса рудничного воздуха, увеличивая фазовый состав рассматриваемой термодинамической системы и приводя к росту межкомпонентных взаимодействий. К подобным случаям можно отнести известный факт [3] нарушения пропускной способности вентиляционных стволов на рудниках ОАО «Алроса» за счет послойного обмерзания их поверхности конденсирующимися парами. Подобные явления успешно предотвращали, обеспечивая орошение стенок вентиляционных стволов концентрированными рассолами из карьерного пространства. Ранее исследователями установлено, что в условиях северных шахт и рудников процесс конденсации влаги в летний период эксплуатации проходит значительно интенсивнее, чем обратный ему процесс испарения в зимний период. Однако в условиях значительно более продолжительного зимнего периода велика вероятность иссушения поверхности горных выработок [4] и создания при этом условий для роста запыленности в выработке [5].
Целью работы является создание расчетной модели, адекватно описывающей процесс влагообмена между вентилируемым воздухом и поверхностью выработки с использованием функций равновесного содержания влаги в воздухе и окружающих породах.
Материалы и методы исследования
В данном контексте представлена математическая модель процесса конденсации влаги на стенках горной выработки, первоначально имеющей отрицательную температуру стенок. При этом, в отличие от ранних работ [5], используются функции равновесного содержания паров воды в рудничном воздухе и незамерзшей влаги в породном массиве, окружающем выработку, как известные из опыта и зависящие от температуры. Использование подобного базиса позволяет существенно повысить методическую точность и адекватность определения параметров состояния рудничной атмосферы выработок криолитозоны и породного массива.
Процесс понижения температуры потока влажного воздуха моделируется уравнением, учитывающим его теплообмен со стенками выработки.
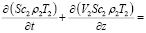
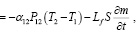(1)
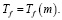
Здесь первый член уравнения (1) представляет собой положительную динамику изменения температуры воздушного потока в выработке за счет конвективного переноса (второй член уравнения (1); понижение температуры потока за счет теплообмена воздушного потока с поверхностью стенок выработки, имеющих отрицательную температуру, и третий член уравнения (1) определяет вклад теплоты фазовых переходов водяного пара в общий энергетический баланс.
Последнее уравнение в системе (1) представляет собой равновесное содержание влаги в рудничном воздухе для различных значений температуры.
Решение системы уравнений (1) строится по упрощенной вычислительной технологии расщепления по физическим процессам [6, с. 85], перечисленным абзацем выше:
а) движение потока воздуха
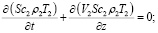
б) конвективный теплообмен с поверхностью породного массива
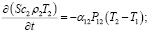
в) учет теплоты фазового перехода при конденсации пара
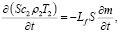
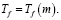
Для параметров уравнений (1 а, в) использованы следующие сокращения: Т1 – температура внутренней поверхности породного массива в выработке оС; S – величина поперечного сечения рудничной выработки в м2; Т2 – температура входящего потока влажного воздуха оС ; Lf – теплота фазового превращения при испарении поровой влаги или льда дж/кг; с2 – теплоемкость рудничного воздуха с учетом содержащихся в нем компонентов дж/(кг.град); V2 – средняя скорость воздушного потока рудничного воздуха м/с; m – весовое содержание влаги в воздухе кг/м3.
Геометрия расчетной области представляет собой внешний граничный контур с размерами 20 м на 20 м с размещенном в центре сечением квадратной выработки размерами с размерами 3 м на 3 м. Выработка и внешний контур размещены в плоскости (x, y), движение воздушного потока осуществляется вдоль оси z. Краевые условия по температуре имитируют тепловое взаимодействие поверхности выработки с потоком рудничного воздуха имеющей на входе в выработку при z = 0 температуру Т2, меняющуюся по синусоидальному закону уравнения
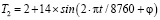. (2)
Считаем, что распределения влаги и температуры в воздушном потоке являются однородными, не зависящими от координат (x, y), следовательно, на границах отсутствует их диффузионный перенос и в балансовых уравнениях (1, а, в) активны лишь конденсационные процессы на поверхностях контакта компонентов вдоль оси z.
Обобщенная математическая модель баланса тепла и влаги в мерзлом породном массиве, представленная в работе [7], адаптирована для рассматриваемого случая породного массива, вмещающего горную выработку. Модель состоит из двух уравнений диффузионного типа с источниковыми членами, отражающими влияние процессов промерзания – оттаивания [7]:
▪ уравнение кондуктивного переноса тепла в породном массиве
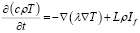, (3)
▪ уравнение диффузионного переноса влаги в породном массиве
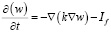. (4)
Уравнение (5) служит дополнительным соотношением, описывающим фазовое состояние незамерзшей влаги в зависимости от параметров породного массива, его температуры и концентрации порового раствора.
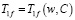. (5)
Решение системы уравнений (3)–(5) осуществляется согласно алгоритму, изложенному в работе [7].
Для решения системы уравнений (3)–(5), так же как и ранее, использована процедура расщепления по физическим процессам в соответствии с [6, с. 85]. В качестве этих процессов выбраны: а) диффузионное выравнивание полей температуры и влажности и б) фазовый переход в термодинамических изолированных подсистемах, составляющих исходную физическую систему. Поэтому решение исходной задачи (3)–(5) представляется в виде последовательного решения подзадач;
а) диффузии:
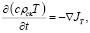
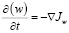; (6)
б) фазового перехода:
,
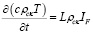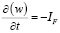. (7)
Система уравнений (7) дополняется уравнением фазового состояния
T1F = T1F(w,C).
Для решения системы (6) с заданными граничными и начальными условиями использован конечно-разностный метод [7] с расщеплением по физическим процессам.
Система (7) определяет действие фазовых превращений на локальные содержания тепла и влаги [7]. Она представляет собой взаимосвязанные уравнения баланса тепла и влагосодержания для термодинамических изолированных подсистем, расположенных в узлах элементарных ячеек сетки Wh. Так как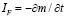 
мощность стока влаги (при превращении вода – лед), то, подставляя его во второе уравнение системы (7), получим для влажности
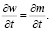(8)
Решая последнее на каждом шаге по времени, получим
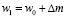, (9)
где 0 и 1 относятся к нижнему и верхнему временным уровням.
Для определения стока влаги Δm на каждом временном шаге используем уравнение теплового баланса (первое уравнение из системы (7)), а также условие, что температура в зоне фазового перехода определяется диаграммой состояния раствора:
,
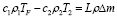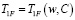. (10)
При этом переход Т1 → T2 определяется решением разностных аналогов системы (6), и температура T2, отражая энергетический баланс процесса, носит фиктивный характер (не учитывает фазовый переход). Переход T2 → T1F определяется решением системы (10). Рассматривая путь Т1 → Тf, полагаем с точностью до бесконечно малых величин первого порядка:
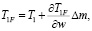(11)
которое определяет изменение состояния (температуры) в замкнутой подсистеме.
После подстановки выражения (11) в уравнение (10), получим, ограничиваясь членами со степенями Δm не выше первой:
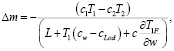(12)
определяя тем самым интенсивность стока влаги в узле при промерзании. Данная методика применима как к фазовым превращениям лед – вода в породном массиве так и к задачам конденсации – испарения.
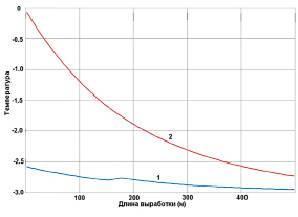
Рис. 1, а. Профиль значений температуры вдоль борта выработки (1) и температура потока воздуха на оси (z) (2)
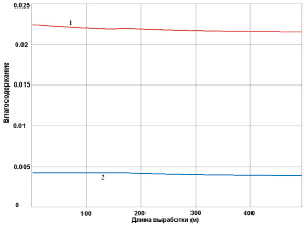
Рис. 1, б. Профиль значений влагосодержания вдоль борта выработки (1) и влагосодержание потока воздуха по оси (z) в (кг/м3) (2)
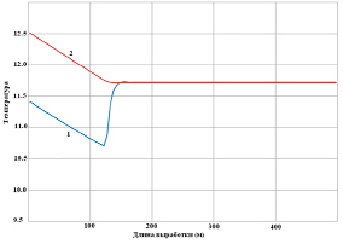
Рис. 2, а. Профиль значений температуры вдоль борта выработки (1) и температура потока воздуха на оси (z) (2)
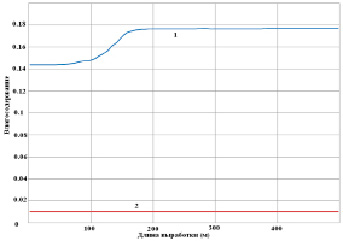
Рис. 2, б. Профиль значений влагосодержания вдоль борта выработки (1) и содержание влаги в потоке воздуха по оси (z) в (кг/м3) (2)
Результаты исследования и их обсуждение
На рис. 1, а, показаны профили значений температуры рудничной атмосферы вдоль оси потока (z) и в борту выработки для начального периода времени ~ 1 ч. Аналогичные результаты для влагосодержания показаны на рис. 1, б. Расчеты показали существенную зависимость интенсивности процесса от коэффициента теплоотдачи (скорости потока) и его входной температуры, то есть второй и третий члены уравнения (1), определяющие количество паровой влаги в единице объема поступающего в выработку воздуха в соответствии с уравнением состояния Тf (m).
На графиках видно, что для начального периода времени характерно интенсивное охлаждение входящего воздушного потока, за счет конденсационных и теплообменных процессов на поверхности горной выработки. Конденсация влаги в рудничной атмосфере носит ограниченный характер и происходит в зоне 100–150 м от входа в выработку, сохраняя тенденцию к росту при наличии плюсового значения температуры воздушного потока на входе.
На рис. 2, а, показаны профили значений температуры рудничной атмосферы вдоль оси потока (z) и в борту выработки для периода времени ~ 1000 ч. Аналогичные результаты для влагосодержания показаны на рис. 2, б. Расчет процесса конденсации влаги из рудничного воздуха подтверждает локальный характер процесса, обусловленный формированием зон конденсации, где значения температуры потока, определяющие равновесное содержание влаги в рудничном воздухе и формирующиеся в условиях нестационарного теплообмена с поверхностью стенок выработки оказываются ниже их равновесных значений. Этот факт и вызывает выпадение влаги, формируя зоны конденсации влаги в выработках на входе в выработку, постепенно смещаясь по направлению движения рудничного воздуха. Длина участка конденсации способна к росту по мере увеличения температуры, влагосодержания и скорости воздушного потока.
В этом случае система близка к квазистационарному режиму теплообмена. Разница между температурой потока воздуха и температурой поверхности выработки составляет ~ 1 oC. Изменение температуры потока и стенки вдоль выработки носит линейный характер по ходу выработки. Из-за практически полного отсутствия конденсационных процессов влагосодержание в воздушном потоке меняется незначительно.
Заключение
Представлена математическая модель тепломассообменных процессов при движении влажного воздуха в горных выработках криолитозоны. Установлены закономерности массообмена влаги, находящейся в рудничном воздухе и взаимодействующей с поверхностью породного массива при конденсационных процессах. Достоверность разработанной модели подтверждается использованием функций равновесного содержания паров воды в рудничном воздухе и незамерзшей влаги в породном массиве, окружающем выработку, как известных из опыта и зависящих от температуры, в соответствии с ранее изложенной методикой. Результатами моделирования процессов переноса в горной выработке установлена форма профилей температуры и содержания влаги в бортах горной выработки и на оси (z) в воздушном потоке. Установлены размеры областей выпадения конденсационной влаги и ее избыточного отложения. Результаты расчетов по представленной модели, основанной на учете функций равновесного содержания влаги в рудничной атмосфере и породном массиве, позволяют строить адекватные картины распределения влагосодержания и температуры в рудничном пространстве и окружающих породах.