Введение
На данный момент основным направлением развития крупных городов является строительство высотных и сверхвысотных многофункциональных комплексов. Объекты такого типа требуют особого подхода к геодезическому обеспечению их возведения [1]. Важнейшей задачей является обеспечение вертикальности сооружения и соосности его несущих элементов. Но высотные здания не остаются неподвижными в течение всего времени строительства. Под действием различных факторов, таких как неравномерный нагрев несущих конструкций и ветровая нагрузка, здания могут испытывать значительные вертикальные и горизонтальные перемещения даже в течение суток.
Одним из решений поставленной выше задачи является комплексное использование геотехнических датчиков, спутниковой геодезической аппаратуры и электронных тахеометров1 [2; 3]. Практическая эффективность такого комплексного подхода, сочетающего ГНСС-наблюдения и высокоточные тахеометрические измерения для мониторинга крена высотных зданий, подтверждена экспериментальными исследованиями [4]. При этом использование GNSS-технологий, интегрированных в системы мониторинга, позволяет обеспечить независимую от высоты точность и постоянный контроль деформаций, что особенно важно для уникальных высотных объектов [5]. Но такое решение требует большого количества аппаратуры, специального программного обеспечения и большого числа высококвалифицированных геодезистов. Кроме того, практика показывает, что даже успешные методики, примененные на знаковых объектах (например, система мониторинга Бурдж-Халифа), не всегда могут быть напрямую адаптированы к другим стройплощадкам из-за уникальных архитектурных, технологических и климатических условий, что требует разработки новых специализированных решений [6]. Также разрабатываются методики, позволяющие определять деформации высотных зданий при помощи анализа спутниковых фотоснимков [7].
Особое внимание уделяется учету температурных деформаций и деформаций, вызванных ветровой нагрузкой [8; 9]. Актуальность этой задачи подчеркивается тем, что в реальных условиях неравномерный нагрев конструкций солнцем приводит к значительным деформациям изгиба, величина которых для высотных зданий может существенно превышать точность, регламентированную нормами на производство геодезических работ [10].
Альтернативным решением может стать компьютерное моделирование деформаций железобетонных конструкций. Работы по моделированию деформаций зданий и работе железобетонных конструкций [11; 12] ведутся достаточно давно.
Основой для моделирования может служить метод конечных элементов (МКЭ), широко применяемый для задач проектирования и расчета несущих конструкций. Данный метод лежит в основе ряда программных комплексов, таких как ПК «ЛИРА-САПФИР», RSTAB 9, SCAD и др. Вопросу о возможности применения подобных программных комплексов для задач моделирования и учета температурных деформаций посвящена данная работа.
Цель исследования – изучение возможности применения компьютерного моделирования и расчетов по методу конечных элементов для задачи учета температурных деформаций высотных железобетонных зданий при геодезическом сопровождении строительства.
Материалы и методы исследования
Прежде всего необходимо определить понятие «моделирование» в соответствии с нормативными документами. Для этого обратимся к ГОСТ Р 57412–2017 [13]. Согласно [13]:
− модель: сущность, воспроизводящая явление, объект или свойство объекта реального мира;
− объект моделирования: явление, объект или свойство объекта реального мира;
− моделирование: изучение свойств и/или поведения объекта моделирования, выполненное с использованием его моделей;
− математическая модель: модель, в которой сведения об объекте моделирования представлены в виде математических символов и выражений;
− компьютерная модель (электронная модель): модель, выполненная в компьютерной (вычислительной) среде и представляющая собой совокупность данных и программного кода, необходимого для работы с данными.
В основе любой модели заложен некоторый математический аппарат. Определить поведение объекта моделирования или его свойства в заданных условиях можно, либо используя формулы, описывающие физику происходящих в нем процессов, либо используя выражения для интерполяции/экстраполяции некоторых величин, основываясь на экспериментальных данных. Подход, основанный на применении формул, описывающих физику процесса теплового расширения высотных зданий и сооружений, применяется для решения геодезических задач довольно давно. Так, в диссертации В.Я. Раинкина «Геодезические работы при строительстве и эксплуатации высотных сооружений башенного типа: на примере Останкинской телевизионной башни» [14, с. 99–163] рассмотрены основные принципы учета перемещений высотных зданий, вызываемых температурными факторами.
В настоящее время этот метод дополнен и усовершенствован. Сейчас для учета деформаций, вызванных температурными факторами, может применяться метод конечных элементов (МКЭ). Согласно ГОСТ Р 57188-2016 [15] Метод конечных элементов – сеточный метод численного решения задач математической физики, в котором дискретизация исходных краевых задач производится на основе вариационных или проекционных методов при использовании специальных конечномерных подпространств функций, определяемых выбранной сеткой. Опираясь на приведенное определение, можно описать суть МКЭ более просто: расчетную область (деталь, конструкцию, объем) разбивают на множество простых мелких частей – «конечных элементов», которые вместе образуют сетку; искомая сложная функция (например, поле перемещений, температур или давлений) аппроксимируется внутри каждого такого элемента с помощью простых кусочно-гладких функций (полиномов); затем для всей системы элементов составляется и решается глобальная система алгебраических уравнений. Ее решение дает приближенные значения искомой функции в узлах сетки и внутри элементов.
Для моделирования и дальнейшей проверки работоспособности модели было выбрано каркасное 23-этажное здание из монолитного железобетона, с архитектурной высотой 90 м. В соответствии с СП 267.1325800.2016 «Здания и комплексы высотные. Правила проектирования» данное здание является высотным, так как имеет высоту более 75 м. Таким образом выбор здания соответствует задачам исследования.
Для моделирования выбран программный комплекс «ЛИРА-САПФИР». Данный программный комплекс имеет весь необходимый функционал для создания трехмерной модели здания, преобразования модели в модель с конечными элементами, задания и расчета нагрузок и вычисления перемещения узлов. Также важно отметить удобный и интуитивно понятный (для опытного пользователя САПР) интерфейс, а также наличие свободно распространяемой некоммерческой версии программы. Важным фактором является и наличие статей по верификации расчетов, выполняемых данным программным комплексом. Данные материалы доступны на официальном сайте программного комплекса. Также применение программного комплекса «ЛИРА» для задач учета температурных деформаций описано в [16]. Возможности современных программных комплексов, включая «ЛИРА-САПФИР», позволяют учитывать поэтапность возведения зданий, что является критически важным для точного моделирования их напряженно-деформированных состояний на всех стадиях жизненного цикла [17].
Для полевых работ использовались следующие приборы:
1. Электронный тахеометр Leica TS06 R500. Основные характеристики:
a) точность угловых измерений 5»;
b) компенсатор двухосевой, диапазон работы ±4’;
c) дальность измерения на одну призму 1,3–3500 м;
d) точность линейных измерений на одну призму ±1,5 мм + 2 мм/км;
e) дальность измерения на отражающую пленку 1,3–400 м;
f) точность линейных измерений на отражающую пленку ±1,5 мм + 2 мм/км;
g) дальность измерений без отражателя 0,3–500 м;
h) точность линейных измерений без отражателя ±2 мм + 2 мм/км;
i) увеличение зрительной трубы 30x.
2. Пирометр RGK PL-7 MAX.
Использование высокоточных электронных тахеометров серии Leica TS, включая более ранние модели (например, TS09), является стандартной практикой при геодезическом сопровождении строительства уникальных и высотных объектов, что подчеркивает их роль в обеспечении точности разбивочных работ и мониторинга [18].
Результаты исследования и их обсуждение
Как было сказано выше, моделирование будет выполняться в программном комплексе «ЛИРА-САПФИР». Данный комплекс состоит из двух программ: «ЛИРА-САПР» и «САПФИР». Непосредственное создание модели по рабочей документации выполнено в программе «САПФИР». При этом работа ведется с такими элементами, как стена, колонна, балка и плита перекрытия, которые не являются конечными элементами и не подходят для расчетов нагрузок и перемещений. Моделирование велось в следующем порядке:
1. Создание строительных осей здания.
2. Создание нового этажа и отрисовка вертикальных несущих конструкций (стен).
3. Создание горизонтальных несущих конструкций (плит).
4. Создание типового этажа и отрисовка вертикальных несущих конструкций (стен и колонн).
5. Копирование типового этажа и редактирование вертикальных несущих конструкций для нетиповых этажей.
В результате моделирования по данным рабочей документации автором была получена полная модель здания (рис. 1) в программе «САПФИР», которая входит в комплекс «ЛИРА-САПФИР»

Рис. 1. Полученная модель здания Примечание: составлен автором по результатам исследования
Важно отметить, что в процессе отрисовки несущих конструкций задавались параметры бетона, соответствующие параметрам, указанным в рабочей документации.
После создания трехмерной модели здания был выполнен ее экспорт в ЛИРА-САПР с преобразованием всех элементов модели в конечные элементы, такие как стержни, узлы и т.п. Модель в конечных элементах представлена на рис. 2.

Рис. 2. Модель в конечных элементах Примечание: составлен автором по результатам исследования
На этом первая задача исследования была выполнена: получена трехмерная модель здания, подходящая для расчета нагрузок и перемещений. Далее проводились полевые работы по определению фактических перемещений марок-катафотов, закрепленных на здании. Схема расположения марок приведена на рис. 3.
Измерения положения геодезических марок, размещенных на здании, выполнялись электронным тахеометром относительно исходных пунктов, закрепленных на несущих стенах первого этажа моделируемого здания.
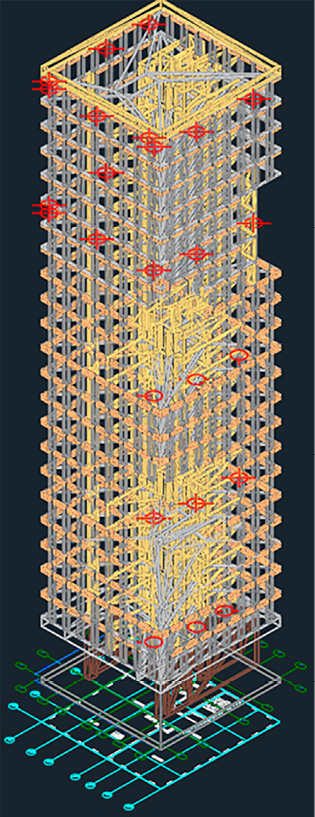
Рис. 3. Схема расположения марок на здании Примечание: составлен автором по результатам исследования
Для определения исходного положения пунктов измерения проводились в пасмурную погоду, когда температура всех элементов здания была одинакова и составляла +6 °С. Для определения деформаций измерения проводились в ясную погоду, когда часть здания была освещена солнцем. Также в этот момент выполнялись измерения температуры несущих элементов здания при помощи пирометра. Для более детального и непрерывного контроля температурного поля конструкции, являющегося ключевым фактором ее деформаций, перспективно применение беспроводных сенсорных систем мониторинга, позволяющих отслеживать распределение температуры в реальном времени [19].
После этого выполнялось моделирование по данным измерения температуры, вычислялись координаты марок в деформированном состоянии, путем сложения координат в недеформированном состоянии и величин перемещений из таблицы перемещений. Моделирование выполняется путем задания соответствующих нагрузок. В данном случае, помимо стандартных нагрузок от собственного веса здания, была задана нагрузка на стержни, называемая в программе «Неравномерный нагрев».
После этого выполнялся расчет при помощи соответствующей команды. После расчета формируются стандартные таблицы отчета, среди которых для данной работы необходима только таблица перемещений.
Марки были размещены на колоннах, которые после экспорта в ЛИРА-САПР были преобразованы в стержни. Места примыкания колон и плит перекрытий преобразованы в узлы. В результате расчета программа позволяет сформировать таблицу перемещений узлов по каждой оси координат. Но так как марки расположены не в узлах, а между ними, то для того, чтобы получить перемещение марки, необходимо выполнить интерполирование величины перемещения по каждой оси между двумя узлами. После этого, прибавив к исходным координатам вычисленные перемещения, были получены координаты марок в деформированном состоянии.
Также рассмотрим структуру таблицы «Перемещения», полученной в результате моделирования (таблица).
Структура таблицы «Перемещения»
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
ЗАГР |
УЗЕЛ |
X, мм |
Y, мм |
Z, мм |
UX, RD*1000 |
UY, RD*1000 |
UZ, RD*1000 |
|
2 |
1 -dT |
|||||||
|
3 |
1 |
3765 |
1,12345 |
0,22235 |
2,55461 |
-0,04885 |
0,22144 |
-0,66511 |
Примечание: составлена автором на основе таблицы «Перемещения» программного комплекса «ЛИРА-САПФИР».
Столбец 1 – номер загружения, обозначает тип нагрузки, вызывающей указанные в следующих столбцах перемещения; 2 – номер узла модели; 3, 4, 5 – перемещения узла из столбца 2 по соответствующим координатам (линейные перемещения в мм), 6, 7, 8 – угловая составляющая перемещения в данном узле.
Для определения перемещений геодезического знака, закрепленного на колонне, необходимо выполнить линейную интерполяцию.
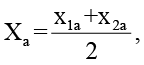 (1)
(1)
где Xa – перемещение отражателя по одной из координат, x1a – перемещение первого узла по соответствующей координате, x2a – перемещение второго узла по той же координате. Важно отметить, что формула (1) справедлива только для случая, когда геодезический знак закреплен в середине колонны. Система координат – локальная система программного комплекса, оси координат параллельны строительным осям здания. Для вычисления полных перемещений геодезического знака с учетом угловых величин необходимо воспользоваться следующими формулами:
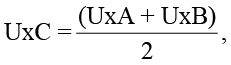 (2)
(2)
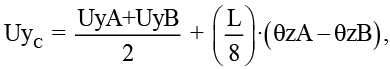 (3)
(3)
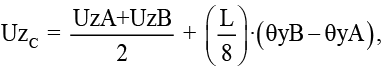 (4)
(4)
где UxC, UyC, UzC – полные перемещения середины стержня, UxA, UyA, UzA – линейные перемещения узла начала стержня (по таблице) UxB, UyB, UzB – линейные перемещения узла конца стержня (по таблице), L – длина стержня, θzA, θzB, θyB, θyA – величины угловых перемещений вдоль соответствующих осей (по таблице). Для первичной проверки модели угловые величины перемещений в узлах не учитывались.
Также важным моментом является оценка точности измерений, выполненных для проверки модели. Положение марок, размещенных на здании, определялось относительно базиса, закрепленного на несущих конструкциях первого этажа того же здания. Этот подход выбран, так как несущие конструкции первого этажа наименее подвержены неравномерному нагреву ввиду расположения здания, а также на их положение не влияют ветровая нагрузка и колебания, вызываемые подъемными механизмами. Также для данной задачи нельзя закреплять точки базиса вне исследуемого здания, так как осадки здания и другие виды деформаций в этом случае будут значительно влиять на качество измерений.
Прибор ориентируется относительно базиса методом обратной линейно-угловой засечки, который широко исследуется и применяется для задач деформационного мониторинга [20]. Схема засечки представлена на рис. 4.
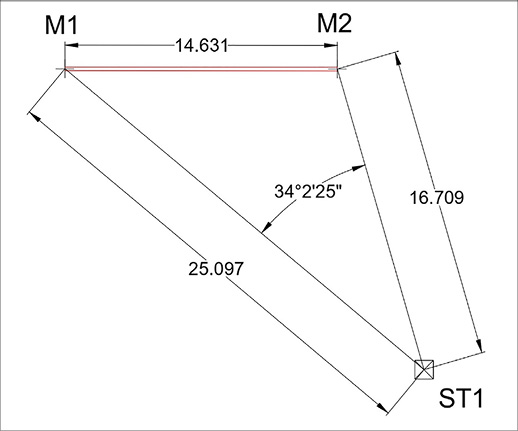
Рис. 4. Схема засечки Примечание: составлен автором по результатам исследования
На схеме ST1 – станция, место установки электронного тахеометра, М1 и М2 – точки базиса. Далее, можно принять координаты базиса безошибочными. Для оценки точности планового положения пункта ST1 воспользуемся формулой [21, с. 208–213]:
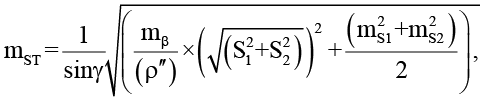 (5)
(5)
где sinγ – измеренный угол между направлениями ST1-M1 и ST1-M2, mβ – СКП измерения угла, ρʺ = 206265ʺ, S1, S2 – расстояния ST1-M1 и ST1-M2 соответственно, ms1, ms2 – СКП измерения расстояний ST1-M1 и ST1-M2 соответственно.
СКП измерения угла принята из технических характеристик прибора, она составляет 5ʺ. СКП измерения расстояний также указана в технических характеристиках прибора, с учетом длин измеряемых линий получено следующее значение: ms1 = ms2 = 1,5 мм. Измеренные величины указаны на рис. 4. Тогда, подставив все имеющиеся значения в формулу (5), mST = 3 мм.
Также нужно оценить точность определения высоты прибора относительно базиса методом тригонометрического нивелирования. Для этого была использована следующая формула [22, с. 752]:
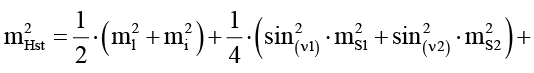
 (6)
(6)
где ml – погрешность измерения высоты отражателя, mi – погрешность измерения высоты прибора, ν1, ν2 – измеренные вертикальные углы, mν – СКП измерения вертикального угла, mH1, mh2 – СКП высотных отметок исходных точек. Развитие методик высокоточного тригонометрического нивелирования с использованием электронных тахеометров позволяет достигать точности, сопоставимой с геометрическим нивелированием II–IV классов, что подтверждает обоснованность его применения для оценки высотных отметок в деформационном мониторинге [23]. Для рассматриваемой ситуации примем ml и mi равными нулю, так как исходные пункты представляют собой геодезические марки, а высота прибора совпадает с высотой определяемой точки, mν = mβ, S1, S2 указаны на рис. 4, ν1 = 4о30ʹ 08ʺ ν2 = 7o 6ʹ 9ʺ, mH1, mh2 примем равными 1 мм. Тогда mHst = 1 мм.
Далее была рассчитана точность измерения координат определяемой точки, по следующим формулам [21, с. 214–215]:
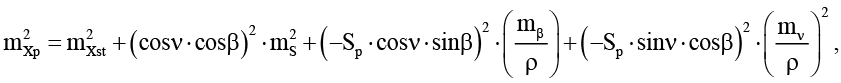 (7)
(7)
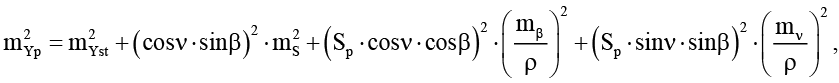 (8)
(8)
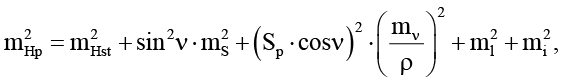 (9)
(9)
где mXst, mYst, mHst – СКП определения координат станции, Sp – расстояние от станции до определяемой точки, β – дирекционный угол направления на точку Р, ν – измеренный вертикальный угол. Для точки, расположенной на 18 этаже, примем: Sp=81,943 м., β = 355о 37ʹ 39ʺ, ν = 67o 27ʹ 05ʺ, mXst = mYs t= 3 мм., mHst = 1 мм. Подставив указанные значения в формулы (7)–(8), после извлечения корня получены следующие значения: mXp = 3 мм, mYp = 3 мм., mHp = 2 мм.
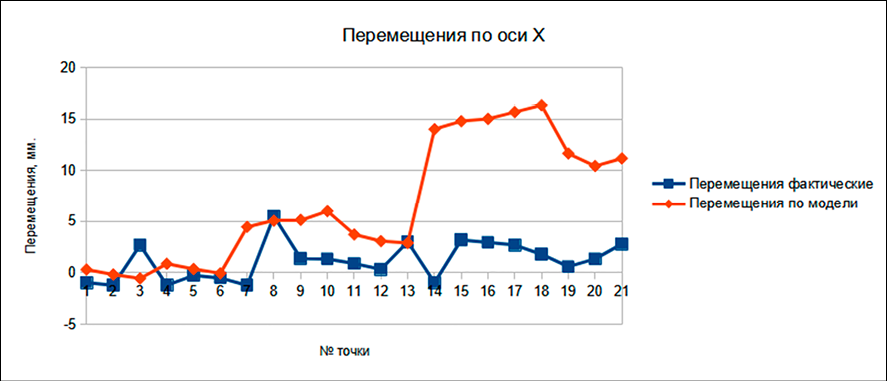
Рис. 5. Диаграмма перемещений по оси Х Примечание: составлен автором по результатам исследования
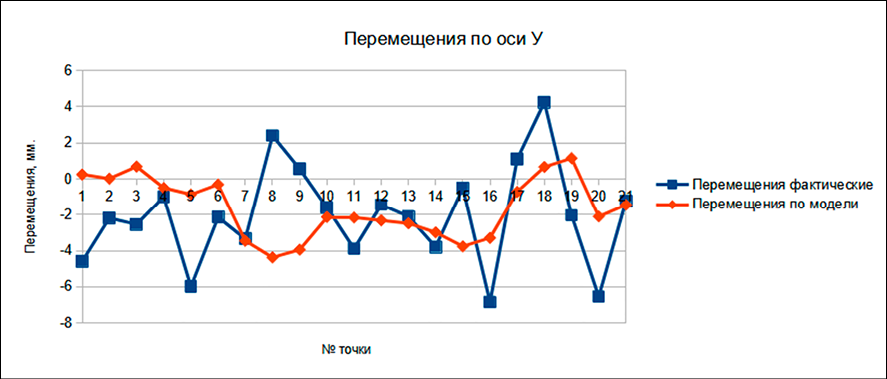
Рис. 6. Диаграмма перемещений по оси У Примечание: составлен автором по результатам исследования
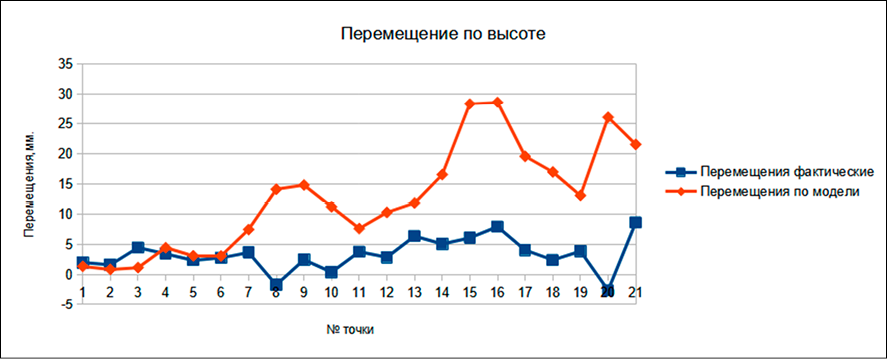
Рис. 7. Диаграмма перемещений по высоте Примечание: составлен автором по результатам исследования
Наиболее удобным для анализа форматом представления данных является диаграмма. Ниже представлены линейные диаграммы величин перемещения марок по каждой оси (рис. 5–7). На каждой обозначены как фактические перемещения, так и перемещения, рассчитанные по модели. Величины перемещений на диаграммах указаны в мм.
Результаты показали, что расчетные перемещения, полученные по модели, коррелируют с фактическими измерениями, при этом наибольшие расхождения наблюдались для марок, расположенных на верхних этажах. Подобные исследования, сочетающие непрерывный мониторинг деформаций в процессе строительства с верификацией конечно-элементных моделей, учитывающих реологические свойства бетона и условия строительства, также подтверждают хорошую корреляцию между расчетом и экспериментом для сверхвысоких зданий [24]. Увеличение расхождения данных модели и измерений может быть связано с тем, что марки с большим порядковым номером расположены на более высоких этажах. С учетом того, что все измерения проводились с земли, а марки расположены вертикально на колонах, можно предположить, что большое расхождение фактических данных и данных модели связано с бо́льшими погрешностями измерений более высоких марок, так как угол падения визирного луча на марки разных этажей различный, что, в свою очередь, вызывает дополнительные погрешности [25]. Экспериментальные исследования подтверждают, что при измерении расстояний в безотражательном режиме на больших углах падения луча (более 40–50°) может возникать систематическая ошибка, что особенно актуально для высоко расположенных марок [26]. Кроме того, при дальнейшей работе над темой необходимо учитывать влияние вертикальной рефракции по алгоритму, предложенному в [27].
Однако, несмотря на большие расхождения перемещений для более высоких марок, для марок нижних этажей расхождения небольшие. С учетом вышесказанного можно сказать, что модель является работоспособной, хоть и требует некоторой доработки, а также необходимо провести эксперимент, который позволит уменьшить погрешности измерения марок на верхних этажах. Перспективным направлением для повышения достоверности геодезического мониторинга высотных зданий является интеграция данных конечно-элементного моделирования с показаниями автоматизированных стационарных систем контроля, например, на основе волоконно-оптических датчиков [28].
Выводы
− Данные компьютерного моделирования позволяют получать информацию о деформациях железобетонного каркаса здания, вызванных тепловым расширением.
− Построенная модель требует доработки, для улучшения моделирования вертикальной составляющей деформаций.
− Для получения более надежных данных измерений, на высоких этажах необходимо разместить уголковые пленочные отражатели или призменные отражатели.
[1] CTBUH (Council on Tall Buildings and Urban Habitat). Инжиниринг самого высокого здания в мире: Бурдж Дубай / пер. с англ. [Электронный ресурс]. URL: https://global.ctbuh.org/resources/papers/download/1326-engineering-the-worlds-tallest-burj-bubai.pdf (дата обращения: 14.11.2025).



