Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

1. Вступление (о названии)

В истории физики от Аристотеля [1] до наших дней использовались многочисленные названия физических теорий, среди которых встречаются лаконичные (динамика, оптика...), составные (термодинамика, гидродинамика, электродинамика...), феноменологические (молекулярная физика, атомная физика...), многословные (специальная теория относительности, релятивистская теория гравитации...), но при внимательном рассмотрении каждого из названий мы вынуждены признать, что все названия являются феноменологическими, так как имеют своим предметом один или комплекс определенных, специально выделенных феноменов природы: взаимодействие тел, течение жидкостей или газов, тяготение...

Одновременно с исследованиями во всех областях многочисленных феноменологических теорий на протяжении всей истории физики учёные каждый раз убеждались, что в действительности ПРИРОДА едина, но многообразна в проявлениях частных своих свойств...

Этим обстоятельством и объясняется стремление физиков с эпохи А. Эйнштейна создать единую теорию поля (ЕТП), в которой бы объединялись законы электродинамики и тяготения, механики и оптики...[1], [2].

Такую теорию следовало бы назвать теорией единого поля (ТЕП), но исторически физика уже накопила знания о свойствах и законах многочисленных феноменов, которые мы называем полями электрическим, магнитным, гравитационным..., поэтому название «ТЕП» приведёт к недоразумениям, вызывая ассоциацию ещё об одном физическом поле...[2], [3]. Вместе с тем, преследуя цель изучить единые, самые общие законы и свойства материальной природы, атрибутами (неотъемлимыми свойствами) которой являются пространство и время, можно в соответствии с традицией использования древнегреческих терминов назвать этот подход стереохронодинамикой (СХД).

2. Происхождение проблемы

26 мая 1917 года Нобелевский лауреат, организатор и председатель Сольвеевских Конгрессов физиков Г. А. Лоренц по просьбе профессора Лейденского Университета П. Эренфеста представил на заседании Амстедамской Академии доклад П. Эренфеста «Каким образом в фундаментальных законах физики проявляется то, что пространство имеет три измерения?», в котором П. Эренфест выразил вековечную мечту мыслителей о ясном представлении себе всех свойств нашего мира [4]. Действительно, задолго до И. Р. Пригожина [5] специалисты из различных отраслей знания заподозрили существование различных размерностей в мирах различной природы: биологи и историки, геологи и химики, математики и философы с изумлением наблюдали такое поведение своих объектов, словно эти объекты находились в пространствах различных размерностей. Яркие примеры, иллюстрирующие этот феномен, можно привести из области физики ядерных сил, поведение которых резко отличается от поведения всех других сил в Природе, а фрактальная геометрия природы Р. Мандельброта [6] наглядно показала объективность такого феномена - зависимость размерности пространства от природы процессов. Совершенно ясно, что с целью исследования этой проблемы прежде всего необходимо обратиться к тем фундаментальным категориям, которые характеризуются размерностью. Как известно, современная топология широко применяет эту величину - размерность для своих категорий множества и многообразия, пространства и континуума, являющихся основными предметами топологических исследований.

3. Естественные модели содержания категорий топологии

Привлекая знания не только топологии, но и естественных наук, здесь с учётом корневых смысловых значений слов приходится отметить всего ПЯТЬ уровней иерархии категорий [7]:

I. Континуумы             (множеств).

II. Множества              (многообразий).

III. Многообразия        (пространств).

IV. Пространства        (миров конкретной природы).

V. Миры                       (взаимодействий конкретной природы).

Особенности этапов эволюции самоорганизующихся систем позволяют нам обозначить эти этапы соответствующими названиями как этапы S - образного закона эволюции систем (ПЯТЬ этапов):

1. самозарождение системы
2. самостановление _ « _
3. самоутверждение _ « _
4. самосовершенствование _ « _
5. самовырождение _ » _

Из последнего нашего вывода об эволюции систем приходится отметить корреляцию иерархии систем и этапов их S - образного закона эволюции, то есть соответствующее усложнение системы с достижением определенного этапа развития. Другими словами, более совершенная система является более сложной, включает в себя больше подсистем, или каждая надсистема является более развитой по отношению своих подсистем. Таким образом, отмечая иерархию миров по степени их развития можно отметить следующие ступени эволюции природы движения:

1. Физические миры.
2. Химические миры.
3. Биологические миры.
4. Психические миры.
5. Социальные миры.

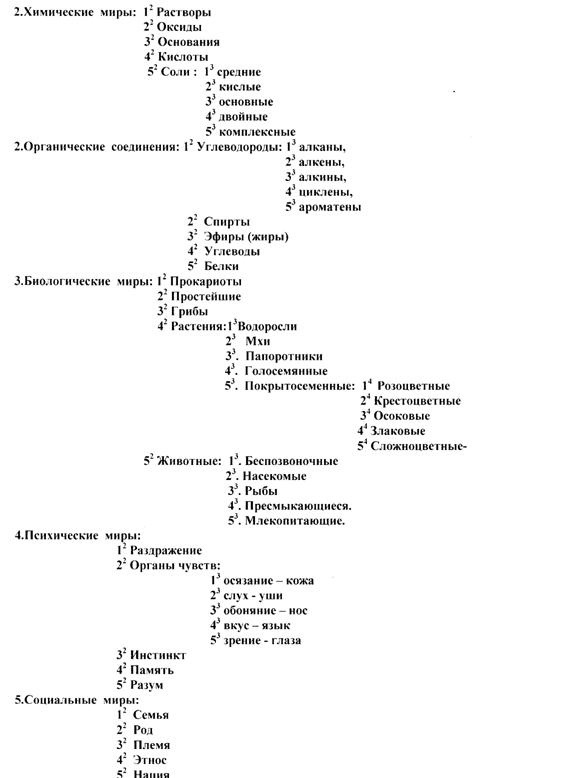
При этом периодичность свойств материальных объектов (частиц, атомов, молекул, кристаллов, растений, животных, социумов...) порождается очередным распространением аналогий форм связей на всех ступенях иерархии. Законы - выражения связей, сохраняясь по форме, наполняются в каждой ступени своим конкретным (физическим, химическим, биологическим, психологическим, социологическим) содержанием. В связи с отмеченным обстоятельством вполне понятна гносеологическая причина значительных затруднений в систематике различных научных дисциплин, которые мы выше заметили, например, в химии (Закон Д, И. Менделеева), в биологии (систематика биологических видов) и т.п. Поэтому представляется целесообразным здесь ввести определенность при указании заданного уровня иерархии, например, арабской нумерацией со скобками, латинским алфавитом, греческим алфавитом и т.п. Из всего обилия возможных вариантов, принципиально равноправных на применение, исходя из практического удобства использования шрифтов и символов условимся латинскую нумерацию (I, II, III, IV, V) оставить за начальным уровнем иерархии, тогда арабская нумерация может применяться для очередного уровня иерархии с указанием степени, соответствующей порядку иерархической ступени, традиционно степень = 1 указывать не будем:

1.Физические миры:

1² Частицы

                  2² Кластеры

                                     3² Ядра

                                                  4² Атомы

                                                                  5² Тела

Примечательным примером периодизации миров является известная периодическая таблица химических элементов Д. И. Менделеева, которая первоначально была им исполнена в виде ПЯТИ периодов. Проведенные в течение XX века различные модификации и усовершенствования этой таблицы на основе продолжающихся новых и новейших достижений атомной физики не могут быть приняты безупречными и окончательными, так как, например, до сих пор не выявлены четкие границы между последовательно заполняющимися электронами энергетическими уровнями, как это мы видели выше на примере плотности вещества в атоме. Но иерархии химических веществ, изученных за много веков, позволяют нам довольно определенно отметить именно ПЯТЬ уровней их иерархии, продолжение которой для всех миров приводит к периодической системе миров:

Например, категорию ЧЕЛОВЕК РАЗУМНЫЙ в этой нумерации можно обозначить, опуская промежуточные ступени, так:

V.Миры:

3¹. Биологические миры:

                                 5². Животные:

                                              5³. Млекопитающие:

                                                                       5⁴ .Приматы:

                                                                                      5⁵ .Человек, то есть: (V-3¹-5²-5³-5⁴ -5⁵)

Невольно на себя обращает внимание обозначение человека ПЯТОЙ ступенью иерархии в биологических мирах - возможно, человек разумный действительно является венцом природы, а не просто так нами принято из наших амбиций?

4. Естественные модели размеров и размерностей в категориях топологии

С естественнонаучной точки зрения [8] определения размерностей , и  в сущности сводятся к следующим выражениям, придерживаясь терминологии и символики первоисточников:

1. Малая индуктивная размерность  пространства Х равна n, если у каждой точки х есть сколь угодно малые окрестности, границы которых имеют размерность n-1 (в смысле ). Размерность пустого множества Ǿ = 0.

2. Большая индуктивная размерность  пространства Х равна n, если для любых его двух не пересекающихся множеств найдётся n-1- мерное замкнутое множество, разделяющее их. Также  Ǿ=0.

3. Размерность  пространства Х, определяемая с помощью покрытий пространства Х, равна n, если минимальная кратность сколь угодно малых покрытий пространства Х равна n+1.

Таким образом, ни одно из этих утверждений, справедливых по существу нахождения величины размерности соответствующих пространств, не может являться определением размерности в логическом смысле, так как логически строгое определение категории, как это мы уже видели на примере определений категорий топологии [7] континуума, множества, многообразия, пространства, требует подведения определяемой категории под более широкое понятие, такую категорию, которая является более общей по отношению к определяемой, отличающейся от боле общего своими частными особенностями. В приведенных выше топологических определениях размерности указывается на принадлежность этой категории к числу, но не указывается нигде на особенности этого числа от других чисел, не являющихся размерностью (числом линий, поверхностей, точек...).

ПЕРИОДИЧЕСКАЯ СИСТЕМА МИРОВ

Так как в работе [8] мы обнаружили, что переходя от уровня к уровню (от вида к виду) иерархии движений, в каждом мире взаимодействие сводится к изменению величины некоторого параметра (расстояния, размера, количества, величины...), то есть: взаимодействие = движение = изменение качества = изменение величины некоторого параметра, то наш вывод, что изменение размерности - суть изменение количества независимых свойств системы (изменение качества системы) означает определение размерности как числа независимых свойств системы, которыми в частном и самом абстрактном случае могут служить в простейшем геометрическом смысле пространственные направления - оси координат, как это представляется на рис. 1 и рис. 2:

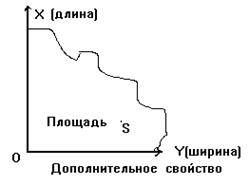
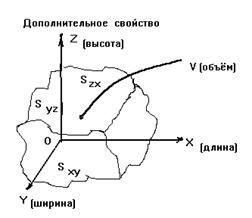
Рис. 1                                                     Рис. 2

Так как размерность является числом независимых свойств, то в случаях гомогенных миров, когда все направления изотропны, можно за координаты принимать геометрические направления под 90^О, то есть применить ортогональную систему координат, так как cos90°=0, а sin90°=1 , позволяя проекциям осей друг на друга превращаться в 0, то есть обеспечивать «независимость». Именно этот смысл - независимость - несёт на себе наше изображение на рис.1 и рис.2 дополнительного свойства по оси под 90^о к заданному направлению уже известного свойства (длины, ширины...)

В случаях гетерогенных миров, когда направления анизотропны, такие условия «независимости» обеспечить невозможно, поэтому и условия «ортогональности» теряют своё значение, в этих мирах координаты по своему происхождению, по своей природе, «по определению» независимы. Например, P,V,T - в законах газового состояния и т.п. А в общем смысле могут быть любые, принимаемые за независимые параметры, как это мы полагаем, например, в функциональных пространствах (PVT закон состояния газов) и т.п., где при углубленном подходе можно показать взаимную зависимость избранных базисных осей-параметров...(вспомним из предисловия в работе [1]:

                  (1).

В качестве наглядной иллюстрации изложенных суждений воспользуемся нашим примером на рис. 3 изменения размерностей из работы [5]:

1. К 1-мерной линии (метр) добавляем новое направление - образуется двумерная плоскость (м²)

2. К 2-мерной плоскости (м²) добавляем новое направление - образуется трёхмерный объём (м³)

3. К 3-мерному объёму (м³) добавляем новое направление-свойство - давление (Па) - образуется функциональное пространство - изотермический процесс по закону Бойля - Мариотта.

4. К 3-мерному объёму (м³) добавляем новое направление - температуру (^оК) - образуется функциональное пространство - изобарический процесс по закону Гей-Люссака.

5. К трёхмерному объёму (м³) добавляем два новых направления - температуру (^оК) и давление (Па) - образуется функциональное пространство - процесс по закону Клайперона-Клаузиуса-Менделеева. Перечисление подобных примеров можно продолжать неопределенно долго, но уже из сказанного можно вполне обоснованно заключить, что всякий раз увеличение размерности путём добавления нового независимого направления приводит к образованию нового качественного состояния системы - функциональному пространству, характеризуемому новой величиной, выраженной в соответствующих новых единицах измерения!

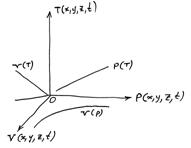
Рис. 3 (Рис. 8 по [8])

Так как единицы измерения длины - одномерной категории не могут быть использованы для измерения площади поверхности - двумерной категории, требующей новых единиц измерения - единиц площади, которые не могут применяться в трёхмерной категории - объёмных телах и т.д., то мы вправе представить себе, что все возможные единицы измерения, как проявления свойств соответствующих категорий являются атрибутом своих категорий, существуют, то есть содержатся в самом понятии категории: способность длины иметь определенную величину в соответствующих единицах длины, способность площади поверхности иметь определенную величину в единицах площади, способность объёма тела иметь определенную величину в единицах объёма и т.д., и т.п.

СПИСОК ЛИТЕРАТУРЫ

1. Вайскопф В. Физика в двадцатом столетии. М., «Атомиздат», 1977.
2. Логунов А. А. «Релятивистская теория гравитации и новые представления о пространстве-времени // Вестник МГУ . Физика. Астрономия. т. 27, вып. 6, 1986, стр.3 и далее.
3. Дирак П. А. Воспоминания о необычайной эпохе, пер. с англ. М., «Наука», 1990, стр.178 и др.
4. Вертинский П.А. Финитность и сингулярность в понятии размерности пространства // VМНС, Красноярск, 2002.
5. Пригожин И.Р. и Стенгерс И. Порядок из хаоса. Новый диалог человека с природой. М., «Прогресс», 1986, стр. 275, 364 и др.
6. Мандельброт Б. Фрактальная геометрия природы. М.: ИКИ, 2002,стр.46, 144, 326.
7. Вертинский П. А. Естественнонаучные модели содержания категорий топологии // Сб.IX МНС, Красноярск,2006.
8. Вертинский П.А. Естественные модели размеров и размерностей в категориях топологии//Сб. X МНС, Красноярск, 2007,
9. Мозерова А., Хайри А., Хузар Ш. Экологическое образование для устойчивого развития // Фундаментальные исследования, № 1, 2009. - C. 97-98.