§ 1. Введение
Излагается разработанная авторами теория предприятия (в макроэкономическом приближении) функционирующего в экономическом пространстве современной России, находящейся в переходном периоде создания многоукладной рыночной экономики.
Взаимодействие экономики предприятия с государственным бюджетом рассматривается через региональные институты экономики субъекта федерации, что в настоящее время имеет место для предприятий основанных на различных формах собственности, в том числе и на смешанной.
Экономическая теория, в том числе и макроэкономическая, претендующая отразить рыночные основания экономической системы, должна иметь конкретную ценность, выражающуюся в важном прикладном значении, конкретно описывать реальные закономерности, основные механизмы, динамику экономических процессов в количественной форме. Конечно в зависимости от "экономики" рассматриваемой задачи, степень её детерминированности или стохастичности разная, но это обстоятельство совершенно не меняет сути, лишь требует владением несколько разными математическими аппаратами.
Макроэкономическая теория любой экономической системы, в том числе предприятия, должна строится на внятной, системе единиц измерения экономических категорий. В нашей конкретной задаче - это рубль (масштаб стоимостного исчисления) и содержательный для экономического пространства задачи масштаб времени. Экономика не может "не знать времени", потому что одной из главных особенностей макроэкономической науки (раздела экономической теории) является тот факт, что она существует только в динамике, только как процесс во времени, неравновесный, необратимый порождающий в экономическом пространстве "стрелу времени". Очевидно, что основное предназначение экономической науки состоит в математическом описании экономических процессов во времени, в нахождении оптимальных траекторий развития исследуемой экономической системы по различным критериям, значимым для общества.
Для характеристики экономических процессов во времени введем два характерных для России отрезка времени: Т = 1 год (время организации экономической статистики) и τ = 10-3 года ( минимальное время формирования макроэкономических категорий). Время τ примем за масштаб (единицу) времени экономического пространства при описании экономической динамики экономической системы (в нашем случае) - предприятия.
Если τ = 1 tec (time economic), то очевидно Т = 103 tec. Поскольку 
t (в точке отрезка 
, где 
) макроэкономическая переменная 
не имеет смысла, т.к. для её существования необходима окрестность τ точки t (функции имеющие смысл только на множестве), постольку производную 
будем понимать как макропроизводную, в которой dt есть макродифференциал, удовлетворяющий условию 
. Конечно и dx есть макродифференциал макроэкономической переменной x(t), соответствующий dt.
Экономическое пространство нашей задачи (до рассмотрения задач оптимального управления, до введения управляющих функций, импульсов) будем понимать [1] как прямое (декартово) произведение положительного ортанда 
n-мерного евклидова пространства 
с прямоугольной системой координат 
- пространства конфигураций на множество Rt - отрезка времени, т.е.
(1.1)
Работа основана на неоклассической идее [5], постулирующей что цель предприятия есть достижение максимума прибыли, т.к. для современной России этот постулат наиболее объективно отражает существующую реальность.
Пусть 
- выпуск продукции, 
- издержки предприятия в единицу времени, тогда прибыль предприятия 
есть
(1.2)
§2. Производственная функция предприятия.
Производственную функцию предприятия будем рассматривать как функциональную зависимость между объемом произведенной продукции в единицу времени q и затратами основного капитала 
, человеческого капитала 
, здесь 
- доля выбывшего основного капитала в единицу времени, 
- средний доход одного работника в единицу времени.
В работах В.К. Булгакова, О.В. Булгакова [2] предложено следующее множество четырехпараметрических 
производственных функций (В - функций)
. (2.1)
Предполагая,
, , K, M = const 
, (2.2)
приходим к выводу, что количество выбывшего за год основного капитала равно 
, а количество затраченного в производстве за год человеческого капитала есть 
, где 
- доля выбывшего за год основного капитала, 
- средний годовой доход одного работника; очевидно, что 
. Обозначим через 
, 
- годовой выпуск, годовую прибыль предприятия.
Предположение (2.2) вытекает из гипотез эргодичности, приемлемости времени T для временного осреднения, более того плотность распределения вероятности макроэкономических переменных x(t) (из-за отсутствия информации) принимается равномерной, нормированной на отрезке = 1 год на 1. В переменных 
запишем найденный в [2] следующий частный класс функций (2.1) - трехпараметрических производственных В-функций
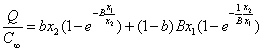. (2.3)
Введя конфигурационную безразмерную переменную
, (2.4)
производственную функцию (2.3) запишем в окончательном для нашей задачи виде
, (2.5)
где
(2.6)
Функция 
, строго вогнутая на 
, 
, имеет горизонтальную асимптоту 
.
§3. Теория издержек производства.
В современной экономической науке популярными являются понятия [4] средних издержек 
и предельных издержек 
производственного процесса предприятия. Отметим, для того чтобы средние издержки не потеряли смысл их необходимо рассматривать на отрезке времени >> τ, для практической пользы возьмем отрезок T = 1 год.
Годовые издержки можно записать в виде
, (3.1)
где τ1 - доля налога на годовой доход коллектива предприятия.
Для определения численности работников предприятия примем гипотизу, что основным фактором, определяющим численность, является величина основного капитала К, участвующего в производственном процессе. Воспользуемся теорией размерности [3]. Из величин 
можно построить следующий отражающий суть вопроса безразмерный комплекс
.
Рассмотрим следующий степенной "закон" численности работников предприятия
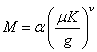, (3.2)
здесь 
- эмпирические постоянные, вычисляемые по статистическим данным группы одного типа предприятий (по продукции и уровню технологического оснащения).
Для расчета 
использован метод наименьших квадратов. Для одного из предприятий общественного питания Хабаровского края, рассмотренного в качестве примера, расчеты дали 
, 
.
Исходя из определения переменных x1, x2, переменной x, используя зависимость (3.2) нетрудно получить
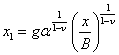(3.3)
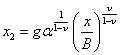(3.4)
Откуда для годовых издержек имеем
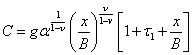(3.5)
Выражение для годового выпуска (2.5) с учетом (3.4) можно записать в виде
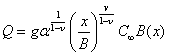(3.6)
Вычисление средних , предельных издержек производственного процесса дает
(3.7)
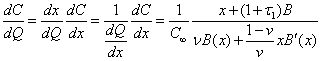(3.8)
При выводе последней формулы использован тот факт, что 
- строго монотонная возрастающая функция, ограниченная на конечном отрезке, вложенном в интервал 
, а также выражения производных
,
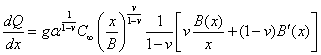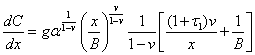
§4. Прибыль предприятия.
Используя (3.6), (3.5) для годовой прибыли предприятия 
получаем
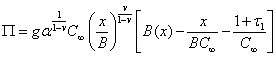(3.9)
В настоящее время в Хабаровском крае РФ налоги изымаются от общей прибыли предприятия. Обозначим через 
величину ставки налогообложения на общую прибыль предприятия, тогда чистая прибыль предприятия в год равна
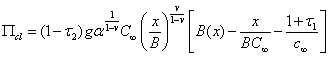(3.10)
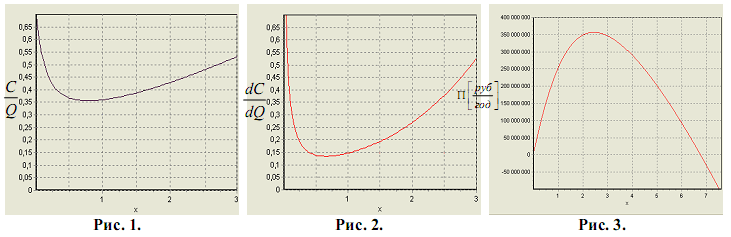
Ниже показаны некоторые результаты расчетов в пространстве . На рис.1 показана зависимость средних годовых издержек 
от переменной x. На рис. 2 показана зависимость предельных издержек от x. На рис. 3 показана зависимость прибыли предприятия в год от переменной x.
§5. Оптимальное управление
Исходя из "закона сохранения" основного капитала
, (5.1)
используя также "темповое" уравнение для среднего дохода одного работника в единицу времени
, (5.2)
для траектории переменной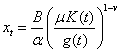 
нетрудно записать следующую задачу Коши
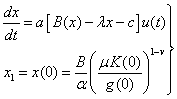, (5.3)
где
,
,
- коэффициент прочих "добровольных" отчислений 
, при этом очевидно, что реальная чистая прибыль предприятия есть 
.
Задача максимума прибыли предприятия есть классическая задача Майера [5,6]
,
где 
- горизонт планирования. В нашем случае решение задачи оптимального управления есть
,
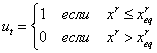где 
определяется в §4. На рис.4 показано оптимальное решение нашей задачи.
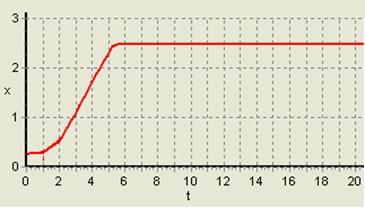
Рис. 4
СПИСОК ЛИТЕРАТУРЫ
- Канторович Л.В, Акилов Г.П. Функциональный анализ. М.: Наука, 1977. 744 с.
- Булгаков В.К., Булгаков О.В. Моделирование динамики обобщающих показателей развития региональных экономических систем России. Экономика и математические методы. 2006. - Т. 42. - №1. - с.32-49.
- Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1987. 432 с.
- Самуэльсон П. А., Нордхаус В.Д. Экономика. Изд. 5. М.: Бином-КноРус, 1999, 800 c.
- Понтрягин Л.С. Избранные научные труды, т.2. Москва: Наука, 576 с.
- Моисеев Н.Н. Численные методы в теории оптимальных систем. М.: Наука, 1974, 424 с.