При математическом моделировании нелинейных волновых процессов возникают нелинейные дифференциальные уравнения в частных производных [1]. Рассматривается нелинейное гиперболическое уравнение 
в области 
, для которого поставлена нелокальная задача с условиями вида
где 
- заданные функции. Доказана справедливость следующей теоремы.
Теорема. Eсли выполняются условия
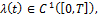
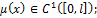
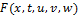непрерывна по всем переменным, 
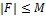;- F удовлетворяет условию Липшица
то существует единственное решение поставленной задачи, принадлежащее классу функций 
и имеющих в Ω непрерывную смешанную производную.
Для доказательства справедливости этого утверждения показано, что поставленная задача при выполнении условия согласования 
эквивалентна операторному уравнению 
где
Найдены условия на входные данные, при выполнении которых оператор L является сжимающим и, следовательно, существует единственное решение уравнения u=Lu. В силу эквивалентности этого уравнения и поставленной задачи тем самым доказана ее однозначная разрешимость.
Работа выполнена при поддержке совместной программы «Михаил Ломоносов» Министерства образования и науки РФ и DAAD.
СПИСОК ЛИТЕРАТУРЫ
- Пулькина Л.С., Климова Е.Н. Об одной нелокальной задаче для нелинейного гиперболического уравнения. Современные методы теории краевых задач. Материалы Воронежской весенней математической школы «Понтрягинские чтения - XVII». - Воронеж: ОАО «Центрально-Черноземное книжное издательство», 2006. С. 151.