Постановка задачи. При проверке статистической гипотезы о том, что функция распределения микроускорений подчиняется гамма-распределению, критерий согласия возрастает почти на порядок при использовании четырех-, восьми- и шестнадцати диапазонного разбиения ( см. рис.1 ).
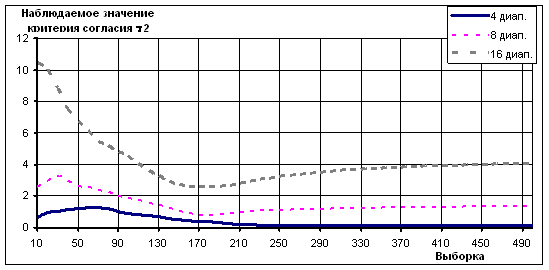
Рисунок 1. Зависимость наблюдаемого значения критерия согласия c2 Пирсона от размера выборки для различного числа диапазонов
Более того, как это отмечено в работах [2] и [3], шестнадцати и более диапазонное разбиение не является характерным для гамма - распределения, - чем выше номер диапазона, тем меньшее число точек должно туда попасть. Однако в десятый диапазон попадает 96 точек, а в одиннадцатый - 130.
Исходя из создавшейся ситуации, можно предположить, что большую роль здесь играет частота выборки данных из непрерывной зависимости микроускорений от времени. Поэтому ставиться задача проверки поведения критерия согласия при десятикратном уменьшении частоты выборки: в предыдущих исследованиях данные выбирались с частотой t1 = 0,01 c., в данной работе - с частотой t2 = 0,001 c.
Основные результаты работы. Уменьшение частоты выборки привело к ожидаемому результату. Критерий согласия для четырех интервального разбиения несколько возрос, тогда как для двух других разбиений, напротив, снизился ( см. рис. 2 ).
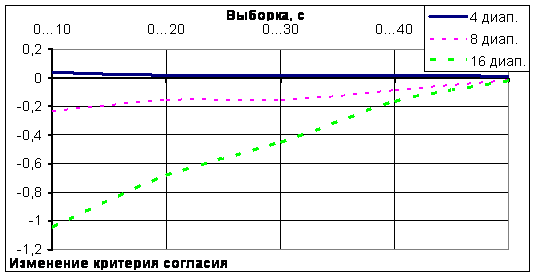
Рисунок 2. Динамика изменения наблюдаемого значения критерия согласия c2 Пирсона от размера выборки для различного числа диапазонов при уменьшении частоты выборки в десять раз
Таким образом, проведенные исследования позволяют сделать вывод о том, что для слишком высокой частоты выборки 0,01с. наиболее характерным с точки зрения критерия согласия является четырех диапазонное разбиение. При уменьшении частоты, в соответствие с правилами статистического анализа, более точные результаты дает разбиение на большее число интервалов.
Анализ предельного уменьшения частоты выборки показывает хорошую сходимость результатов всех трех разбиений, следовательно, возникшее противоречие вызвано только большой частотой выборки данных, а не другими факторами.
СПИСОК ЛИТЕРАТУРЫ
- Седельников А.В., Бязина А.В. Исследование законов распределения микроускорений, смоделированных с помощью функции Вейерштрасса-Мандельброта и полученных в результате эксперимента // Современные проблемы механики и прикладной математики. Сборник трудов международной школы-семинара. - Часть 1. - Т2. - Воронеж. - 2004. - с. 450-453.
- Седельников А.В. Статистические исследования микроускорений как случайной величины // Фундаментальные исследования. - 2004. - № 6. - с. 123-124.
- Седельников А.В. Исследование функции распределения уровня микроускорений во времени // Успехи современного естествознания. - 2004. - № 9. - с. 15-18.



