(1)
где 
- заданные квадратные матрицы размера 
. Приведем некоторые из них: задача нахождения общей функции Ляпунова линейных систем, задача анализа устойчивости системы случайной структуры при неизвестных вероятностях перехода, устойчивость систем, описываемых дифференциальными включениями. Вопрос о разрешимости системы неравенств Ляпунова играет в этих задачах такую же роль, как и вопрос о разрешимости уравнения Ляпунова при исследовании устойчивости обычных линейных систем.
Для численного решения задач подобного рода созданы эффективные программные средства. В то же время аналитические результаты в данной области крайне малочисленны по причине высокой сложности проблемы, и, к тому же, имеют ограниченное применение.
Авторами предложен подход, позволяющий получить аналитические условия существования общей функции Ляпунова для конечного множества линейных систем второго порядка. Рассмотрим множество линейных систем, описываемых стохастическими дифференциальными уравнениями Ито
(2)
где 
- стандартный винеровский процесс с приращениями, не зависящими от начального состояния системы. Требуется найти условия, при которых квадратичная форма 
является общей стохастической функцией Ляпунова для всех систем (2). Эти условия сводятся к условиям разрешимости системы неравенств более общего вида, чем (1), относительно матрицы 
:
(3)
Приведенные далее результаты относятся также и к задаче о существовании общей стохастической функции Ляпунова в виде квадратичной формы для множества дискретных систем
где 
- стандартный дискретный гауссовский белый шум, не зависящий от начального состояния системы. Соответствующие линейные матричные неравенства имеют вид
(4)
Пусть 
, 
- линейные матричные неравенства вида (3) или (4). Пусть 
- матрицы 
из соотношения
где 
. Важную роль в приведенных далее результатах играет выпуклая линейная комбинация матриц :
Теорема 1. Система двух или трех матричных неравенств
имеет решение тогда и только тогда, когда выполняются следующие условия:
- каждое из неравенств имеет решение ;
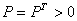- не существует вырожденной выпуклой линейной комбинации матриц , .
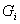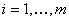Теорема 2. Система из более трех матричных неравенств ,
, имеет решение тогда и только тогда, когда имеют общее решение любые три из этих неравенств.
Проверка существования вырожденной выпуклой линейной комбинации для двух или трех неравенств осуществляется с помощью следующих теорем.
Теорема 3. Если при 
выполняется первое условие теоремы 1, то вырожденная выпуклая линейная комбинация матриц 
и 
существует тогда и только тогда, когда полином
имеет вещественный положительный корень.
Теорема 4. Если при 
выполняется первое условие теоремы 1, то вырожденная выпуклая линейная комбинация матриц , и 
существует тогда и только тогда, когда верно хотя бы одно из следующих утверждений:
- неравенства
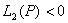и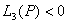 
не имеют общего решения; - полином
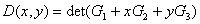имеет нули в первом квадранте
.
Рассмотренные задачи - это задачи анализа. Не меньший интерес представляют проблемы синтеза, в которых нужно найти закон управления, обеспечивающий одновременную стабилизацию семейства систем
(5)
В этом случае мы приходим к следующей задаче: найти матрицы 
и 
такие, что
Данная задача не является тривиальным обобщением рассмотренной выше, но есть уверенность в том, что предложенный подход позволит получить конструктивное ее решение.
Задача одновременной стабилизации стохастических систем приводит к матричным неравенствам более сложного вида:
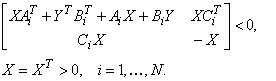(6)
Подобные линейные неравенства повышенной размерности возникают и в других задачах теории управления, в частности, при исследовании систем с запаздыванием.
Таким образом, предполагаются следующие этапы дальнейшего исследования в данном направлении:
- Получение аналитических критериев существования решения задачи одновременной стабилизации систем вида (5).
- Получение аналитических критериев существования решения задач, приводящих к линейным матричным неравенствам повышенной размерности, в частности, к неравенству (6) в задаче одновременной стабилизации стохастических систем.
Работа выполнена при частичной финансовой поддержке РФФИ (грант 02-01-00220) и федерального агентства по образованию (грант А04-2.8-947)