Крупногабаритные плоские газостатические опоры могут найти применение для горизонтальной транспортировке тяжелых грузов. Определенный интерес представляют такие опоры эллиптические в плане формы. Сведения о методах их расчета авторам не известны.
В данной работе излагается метод расчета эллиптической в плане c полуосями a и b (a>b) газостатической опоры с центральным карманом эллиптического сечения c полуосями a* и b* 
, газ в который подается через подводящий канал, площадь сечения которого 
под давлением 
. Давление окружающей среды 
, толщина смазочного слоя H принимается постоянной. Поле квадрата давлений p2 в смазочном слое удовлетворяет уравнению Лапласа 
. Поэтому определение функции p2 может быть сведено к решению краевой задаче для аналитической функции комплексного переменного 
,
, (1)
где x и y - декартовы координаты точки смазочного слоя, а 
- ее комплексная координата, 
- функция тока.
В рассматриваемой задаче поле давлений в смазочном слое определяем с учетом краевых условий
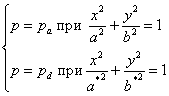(2)
- давление на выходе из кармана, подлежит определению в процессе решения задачи из условия поэлементного сопряжения потоков на общей границе кармана и смазочного слоя 
. Давление в кармане принимаем неизменным и равным 
.
Для решения поставленной задачи, используем методы теории функций комплексного переменного. Эллиптическое кольцо в комплексной плоскости z c помощью функции 
, обратной функции Жуковского (
), может быть отображено на круглое кольцо в плоскости 
. Эта функция ставит во взаимно однозначное соответствие точкам внутренней области эллиптического кольца, точки внутренней области круглого кольца с радиусами 
и 
.
Если принять, что толщина слоя смазочного слоя в фиктивном потоке такая же, как и в реальном потоке, а газ имеет те же термические параметры, что и в реальной опоре, то в соответствующих точках этих опор будет выполняться равенство давлений при соответствующем равенстве их граничных значений. Сохраняется также равенство величин расходов газа через соответствующие контуры. При этом для комплексного потенциала круглой газостатической опоры с центральным питателем в плоскости имеем
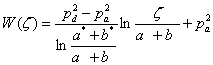(3)
Для определения давления 
на выходе из кармана используем условие равенства расходов газа через питатель и смазочный слой.
Расход газа через круглую опору определяется по формуле
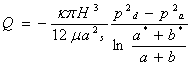, (4)
а расход через подводящий канал вычисляется по формуле
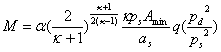. (5)
Т.о. получаем уравнение 
, где 
- газодинамическая функция [1], 
.
Несущая способность смазочного слоя эллиптической опоры определяется по формуле
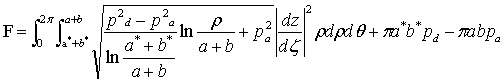, (6)
где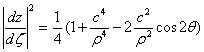 
- якобиан перехода.
По изложенному алгоритму был выполнен расчет эллиптической опоры со следующими параметрами a=10 м, b=5 м, a*=9 м, b*=2,45 м, 
Н/м2 , 
Н/м2 , 
м, 
(м).
Расчет показывал, что при м рабочий зазор в смазочном слое находится в диапазоне 
(м), при этом 
(кг/с), 
(H).
СПИСОК ЛИТЕРАТУРЫ
1. Снопов А.И., Ларикова Н.А., Миронова Е.В. Моделирование газостатических опор с неравномерным дискретным поддувом. // "Современные проблемы науки и образования" №6, 2009 г. С. 34-36