Рассмотрим дифференциальное уравнение вида
(1)
где λ - спектральный параметр, функция q(x) называется потенциалом.
Дифференциальное уравнение (1) мы будем рассматривать вместе с граничными условиями следующего вида:
(2)
где 
Мы будем предполагать, что потенциал является суммируемой функцией на отрезке 
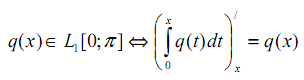почти всюду на отрезке . (3)
Дифференциальное уравнение (1) и граничные условия (2) задают дифференциальный оператор с суммируемым потенциалом.
Для изучения асимптотики собственных значений краевых задач, связанных с дифференциальным оператором (1)-(2), необходимо знать асимптотику решений дифференциального уравнения (1).
Пусть 
- некоторая фиксированная ветвь корня, выбранная условием 
. Пусть 
- корни десятой степени из единицы, то есть
Числа находятся на единичной окружности и делят её на десять равных частей, причём 
Справедливо следующее утверждение.
Теорема 1. Общее решение дифференциального уравнения (1) имеет следующий вид:
, 
(4)
где 
- произвольные постоянные, 
- линейно независимые решения дифференциального уравнения (1), причём при 
справедливы следующие асимптотические разложения:
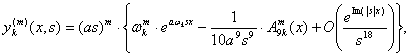
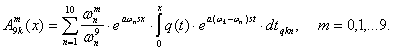(5)
При этом справедливы следующие формулы:
(6)
Идею разложения вида (5) мы изложили в главе 5 монографии [1].
Автором разработан метод нахождения асимптотики собственных значений и асимптотики собственных функций краевых задач типа (1)-(2) при условии выполнения (3). Для случая n=2, другой метод был продемонстрирован в работе [2].
Теорема 2. Решение y(x,s) дифференциального уравнения (1) является решением следующего интегрального уравнения Вольтерра:
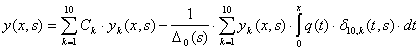, (7)
где yk(x,s) (k=1,2,...,10) - линейно независимые решения дифференциального уравнения (1) при условии 
, 
- определитель Вронского этих решений: 
, при этом несложно доказать, что не зависит от x.
Из формулы (7) методом последовательных приближений Пикара можно вывести асимптотику решений дифференциального уравнения (1). При этом получатся формулы (4)-(5)-(6) теоремы 1. Для дифференциального оператора четвёртого порядка это было проделано автором в работе [3].
Подставляя формулы (4)-(5)-(6) в граничные условия (2), приходим к выводу, что верно следующее утверждение.
Теорема 3. Уравнение на собственные значения дифференциального оператора (1)-(2)-(3) имеет следующий вид:
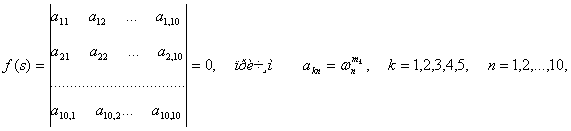
(8)
С помощью свойств определителей доказывается следующая теорема.
Теорема 4. Уравнение (8) имеет следующий вид:
(9)
В уравнении (9) введены следующие обозначения:
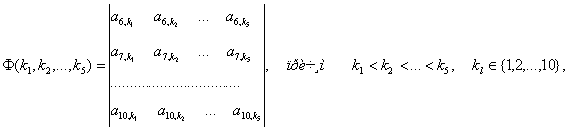
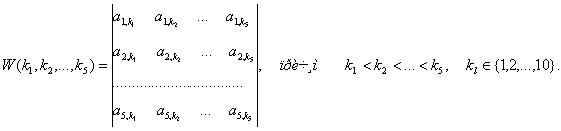
Справедливы следующие формулы:
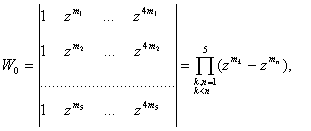
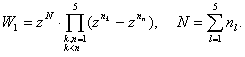
Методами работ [1] и [3] доказывается следующая теорема.
Теорема 5. Асимптотика собственных значений краевой задачи (1)-(2)-(3) в первом секторе индикаторной диаграммы имеет следующий вид:
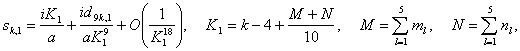(10)
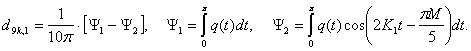(11)
Формулы, аналогичные формулам (10)-(11), для краевых задач типа
(1)-(2)-(3), получены автором и для случаев дифференциальных операторов шестого и восьмого порядков.
Формул (10) и (11) достаточно для вычисления первого регуляризованного следа дифференциального оператора (1)-(2)-(3).
СПИСОК ЛИТЕРАТУРЫ
- Митрохин С. И. Спектральная теория операторов: гладкие, разрывные, суммируемые коэффициенты. М.: ИНТУИТ, 2009. - 364 с.
- Винокуров В. А., Садовничий В. А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Серия: матем. - 2000. - Т. 64, №4. - С. 47-108.
- Митрохин С. И. Асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами. - Вестник Моск. ун-та. Сер.1, математика, механика. - 2009. - №3. - С. 14-17.