, (1)
где 
,
,
- соответственно матрица масс и приведенных моментов инерции, матрица коэффициентов демпфирования и матрица коэффициентов жесткостей звеньев МС; 
- вектор ускорений обобщенных координат (количество координат равно числу степеней свободы всех рассматриваемых звеньев МС), однозначно определяющих положение всех частей МС;
- вектор разностей скоростей обобщенных координат взаимодействующих масс МС;
- вектор разностей перемещений обобщенных координат взаимодействующих масс МС;
- вектор функций обобщенных сил, действующих на обобщенные координаты; t - текущее время.
Для вывода системы дифференциальных уравнений вида (1) на практике широко применяется уравнение Лагранжа второго рода вида:
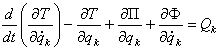, (2)
где Т - кинетическая энергия МС; П - потенциальная энергия МС; Ф - диссипативная функция, характеризующая уменьшение энергии с течением времени; Qk - обобщенная сила, соответствующая k-ой обобщенной координате
; 
- скорость обобщенной координаты.
Известно, что уравнение (2) справедливо для МС с голономными связями. Для исследования движения неголономной системы теоретические разделы механики требуют применения специальных уравнений, например, уравнение Аппеля или уравнений, получаемых из дифференциальных вариационных принципов механики, что затрудняет проведения анализа динамики конструкции МС. Более того, на практике многие МС могут быть как голономными, так и неголономными в зависимости от режимов работы МС. Например, у большого количества машин в трансмиссиях имеются фрикционные муфты сцепления. При работе с блокированной муфтой сцепления мы имеем голономную МС, а при ее буксовании появляется неголономная связь. В данном случае актуален вопрос о возможности применения уравнения (2) для таких неголономных систем.
При появлении подобной неголономной связи предлагается рассматривать МС как комбинацию ее двух частей с голономными связями, соединенных между собой некоторой активной силовой связью 
(рисунок). Пусть силовое взаимодействие этих частей осуществляется между выходными элементами первой части (выходной вал, ведущие детали муфты сцепления и т.п.) и входными элементами второй части МС (входной вал, ведомые детали муфты сцепления, исполнительные механизмы рабочих органов и т.п.). Силовая связь 
при математическом описании работы МС может иметь сложный характер и представлять собой сумму крутящих моментов и сил, зависящих как от обобщенных координат соединяемых элементов 
(позиционные силы, например, сила упругости), так и от их скоростей 
(силы сопротивления, например, демпфирования, трения и т.п.) и ускорений (силы инерции).
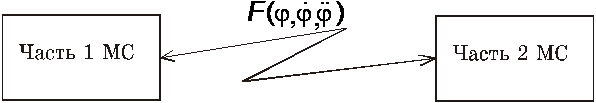
Рисунок 1. Упрощенная структурная схема МС
Схематическое разделение машины на две составляющие ее части позволяет раздельно разрабатывать математические модели различных режимов работы МС для составляющих ее частей с помощью уравнения Лагранжа второго рода (2). Система дифференциальных уравнений, описывающая работу МС в целом, получается путем простого добавления к системе дифференциальных уравнений, соответствующей первой части МС, системы уравнений, описывающей работу второй части МС, с учетом силовой связи 
между обобщенными координатами соединяемых элементов этих частей машины.
В этом случае количество уравнений, описывающих движение МС, будет больше, в сравнении с применением уравнения Аппеля. Но при численных методах интегрирования на ПЭВМ систем дифференциальных уравнений типа (1) наиболее рационально иметь избыточные дифференциальные уравнения и универсальный подход к построению математических моделей МС с голономными и неголономными связями, чем применять более сложный и трудоемкий математический аппарат разработки математических моделей (систем дифференциальных уравнений) динамики МС.