Базовые элементы математической модели МЭЗ [1]:![]() - функция поставок маслосемян подсолнечника;
- функция поставок маслосемян подсолнечника; ![]() - функция среднерыночной цены маслосемян подсолнечника;
- функция среднерыночной цены маслосемян подсолнечника;![]() - функция цены продаж подсолнечного масла;
- функция цены продаж подсолнечного масла;![]() - функция цены продаж подсолнечного шрота;
- функция цены продаж подсолнечного шрота; ![]() - функция продаж подсолнечного масла;
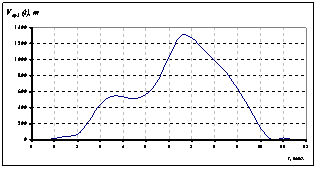
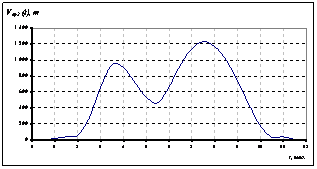
- функция продаж подсолнечного масла; ![]() - функция продаж подсолнечного шрота. Интервал управления - сельскохозяйственный год по маслосемянам подсолнечника (начало года - август). На рис.1-4 представлены графики заданных функций математической модели (рис.→0) вместе с аппроксимирующими их разложениями (рис.→1), ограниченными первыми 20-тью суммовыми членами (погрешность аппроксимации
- функция продаж подсолнечного шрота. Интервал управления - сельскохозяйственный год по маслосемянам подсолнечника (начало года - август). На рис.1-4 представлены графики заданных функций математической модели (рис.→0) вместе с аппроксимирующими их разложениями (рис.→1), ограниченными первыми 20-тью суммовыми членами (погрешность аппроксимации![]() ) [2].
) [2].
|
Рисунок 1. Функция среднерыночной цены маслосемян подсолнечника |
Рисунок 2. Функция цены продаж подсолнечного масла |
|
Рисунок 3. Функция цены продаж подсолнечного шрота |
Рисунок 4. Функции продажи подсолнечного масла |
Начальные условия моделирования [1]: ![]() = 1 750 т/мес.;
= 1 750 т/мес.;![]() = 1439т/мес.;
= 1439т/мес.;![]() = 1,3259;
= 1,3259;![]() = 1,0902;
= 1,0902;![]() =
= ![]() =
= ![]() = 0 т;
= 0 т; ![]() =
= ![]() =
= ![]() = 0 т;
= 0 т;![]() = 40 000 т;
= 40 000 т;![]() = 1 750 т.;
= 1 750 т.; ![]() = 1 450 т;
= 1 450 т;![]() = 1 700 000руб./мес.;
= 1 700 000руб./мес.;![]() = 30 руб./(т∙мес.);
= 30 руб./(т∙мес.); ![]() = 20 руб./(т∙мес.);
= 20 руб./(т∙мес.);![]() =30 руб./(т∙мес.); A = 431 250 руб./мес.;
=30 руб./(т∙мес.); A = 431 250 руб./мес.;![]() =
= ![]() = 0,5 мес.;
= 0,5 мес.; ![]() =
= ![]() = 1,3 мес.;
= 1,3 мес.;![]() =
= ![]() =
= ![]() = 10%;
= 10%;![]() = 18%;
= 18%;![]() = 24%;
= 24%;![]() .
.
Проведенные эксперименты численного моделирования показали:
- для обеспечения сходимости получаемых в форме [2;(6)] приближений к оптимальным функциям управления [1;(1),(2)-(5)] в разложениях [2;(6)] достаточно удерживать только четные члены ряда Фурье (
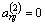 ,
, 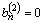 ,
, 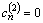 ) при шаге отслеживания состояния базовых элементов модели
) при шаге отслеживания состояния базовых элементов модели 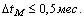 ;
; - приемлемая точность получаемого решения задачи оптимального управления [1;(1),(2)-(5)] в разложениях для оптимизируемых функций управления [2;(6)] достигается удержанием не менее 20-ти суммовых членов ряда Фурье при четных гармониках
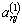 ,
,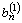 ,
,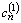 соответственно.
соответственно.
На рис.5-12 представлены графики разложений [2;(6)], аппроксимирующих оптимальные функции управления - выпуска готовой продукции ![]() , закупки сырья
, закупки сырья ![]() и кредитования
и кредитования ![]() , а также функции состояния базовых элементов математической модели ФХД МЭЗ [1] для варианта сочетания собственного и заемного капитала моделируемого предприятия в начале интервала управления: B0 = 20 000 000 руб.,K0 = 80 000 000 руб.
, а также функции состояния базовых элементов математической модели ФХД МЭЗ [1] для варианта сочетания собственного и заемного капитала моделируемого предприятия в начале интервала управления: B0 = 20 000 000 руб.,K0 = 80 000 000 руб.
|
Рисунок 5. Оптимальная функция выпуска подсолнечного масла |
Рисунок 6. Оптимальная функция кредитования |
|
Рисунок 7. Оптимальная функция поставок маслосемян подсолнечника |
Рисунок 8. Функция платежного баланса предприятия |
|
Рисунок 11. Функция состояния запасов маслосемян подсолнечника |
|
|
Рисунок 9. Функция состояния склада подсолнечного масла |
Рисунок 10. Функция состояния склада подсолнечного шрота |
СПИСОК ЛИТЕРАТУРЫ
- Гуров Д.О. Оптимизационная математическая модель финансово-хозяйственной деятельности предприятия. Современные сложные системы управления (HTCS´2004): Материалы IV международной конференции. - Тверь: ТГТУ, 2004. - с.243-247.
- Гуров Д.О. Задача оптимизации финансово-хозяйственной деятельности предприятия в рядах Фурье. Современные сложные системы управления (HTCS´2004): Материалы IV международной конференции. - Тверь: ТГТУ, 2004. - с.248-252.
- Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.




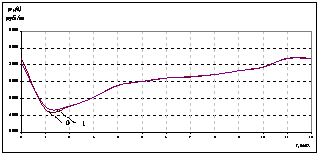
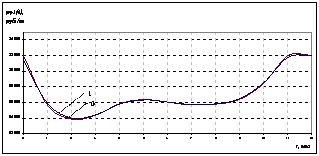
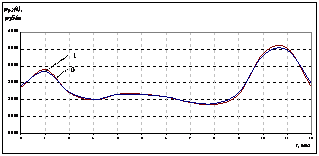
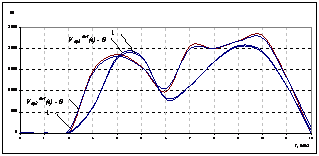
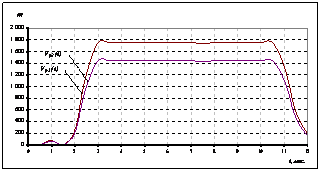
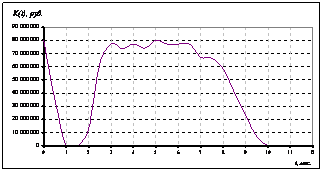
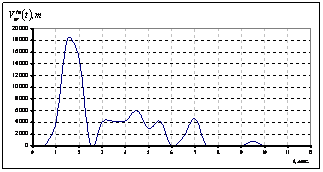
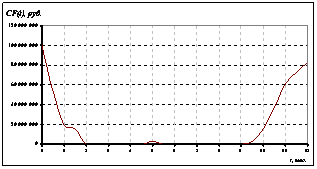
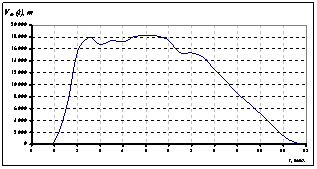
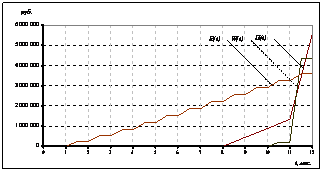 Рисунок 12. Функции ЕСН
Рисунок 12. Функции ЕСН