Определению величины работы выхода веществ посвящено большое число работ [1], однако их результаты получены для достаточно больших по размерам образцов и не могут быть прямо перенесены на мелкодисперсные системы.
Одно из первых объяснений физической природы работы выхода металлов было предложено Дебаем и Шоттки, считавшими ее как работу, совершаемую против сил взаимодействия электрона с индуцированными им на поверхности металла зарядами, то есть против поляризационной силы (силы электрического изображения):
F = e2/4x2, (1)
где x - расстояние от поверхности металла.
Полагал, что работа выхода и есть работа против этих сил, Шоттки и Ленгмюр получили для нее выражение [2]:
W = eφ = e2/2ℓ, (2)
где ℓ - критическая длина, порядка атомного размера, до которой выполняется (1). Квантово-механическое рассмотрение Бардиным поляризационных изменений энергии электронов в металле привело к выражению, совпадающему с формулой (2) [2].
Однако, как показали исследования, работа против поляризационных сил является только частью работы выхода, к которой приводила теория металлов Зоммерфельда. Дополнительной причиной, вызывающей скачек потенциала на границе металла, является двойной электрический слой на его поверхности. Возникновение его объясняется как с классической, так и с квантово-механической точки зрения [2].
Предпринималось много попыток теоретических расчетов работы выхода, однако как показывает анализ [1], рассчитать работу с удовлетворительной точностью не удается. В сложившейся ситуации часто при анализе изменения работы выхода оперируют только с ее поляризационной частью, которая составляет основную часть работы выхода, и которая хорошо моделируется с помощью сил электрического изображения.
При переходе к дисперсным средам добавляются сложности, связанные с их размерными свойствами. Рассмотрим вопрос об изменении работы выхода частиц металлов от их размеров, используя только поляризационную часть работы выхода с использованием формулы (2). В качестве ℓ выберем среднее расстояние между атомами d. Именно до таких расстояний (~ 0,3 нм) было экспериментально проверена формула (1) [3]. Поскольку сила изображения (1), строго говоря, справедлива только для взаимодействия заряда с плоской поверхностью, то при расчетах использовалась также точное выражение для силы взаимодействия точечного заряда с проводящей сферой [4]:
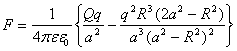 , (3)
, (3)
где q, Q - точечный заряд и заряд сферы соответственно, R - радиус сферы, а - расстояние от точечного заряда до центра сферы.
Из формулы (2) видно, что работа выхода равна удвоенному потенциалу силы изображения в точке ℓ (в системе СИ): Uиз = - e2/(16πεε0ℓ) (4)
Аналогичным образом для определения работы выхода с использованием силы (3) будем брать ее удвоенный потенциал, который определяется формулой:
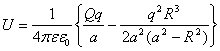 . (5)
. (5)
При этом имеет место соотношение: ℓ = a - R .
Поскольку, вводимые в плазму частицы материала заряжаются и участвуют в теплообмене с плазмой в заряженном состоянии, то необходимо рассмотреть вопрос об изменении работы выхода с изменением заряда частицы. Заряженная частица создает вокруг себя электрическое поле, и в потенциале (4) появится дополнительно кулоновский потенциал:
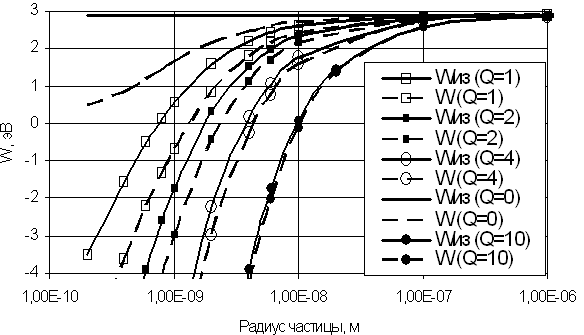
Таблица 1. Зависимость поляризационной части работы выхода W частиц от их размеров и заряда Q
Была рассчитана зависимость работы выхода металла от радиуса частицы для d = 0.25 нм. Соответствующие результаты приведены на рисунке (при Q = 0). Из рисунка видно, что заметный размерный эффект изменения работы выхода (в данном случае, ее уменьшение) появляется для частиц радиуса R < 10 нм, а формула для силы изображения (1) точно описывает силовое взаимодействие электрона с частицами радиуса R > 0.1 мкм. При отрицательном заряде частиц их работа выхода уменьшается. Начиная с заряда частиц Q = 10е и выше в расчетных формулах превалируют кулоновские члены, и они дают практически одинаковые результаты.
СПИСОК ЛИТЕРАТУРЫ
- Фоменко В. С., Подчерняева И. А. Эмиссионные и адсорбционные свойства веществ и материалов. М.: Атомиздат, 1975. 320 с.
- Добрецов Л. Н., Гомоюнова М. В. Эмиссионная электроника. М.: Наука,1966. 564 с
- Термоэмиссионные преобразователи и низкотемпературная плазма / Под. ред. Б. Я. Мойжеса и Г. Е. Пикуса. М.: Наука, 1973. 480 с.
- Смайт В. Электростатика и электродинамика. М.: ИЛ, 1954. 604 с.



