В работе [2] показано, что реально получаемым ЭТ соответствует модель трапециевидного профиля с запыленными боковыми поверхностями. Причем их угол наклона сильно влияет на относительную интенсивность дифракционного спектра. В плоскости падения излучения решение получено в приближении скалярной теории дифракции на поверхности сложной формы, представляющей собой трапециевидную периодическую структуру с периодом d, нижним основанием трапеции (a+b), верхним основанием трапеции b и высотой трапеции h. Эффект взаимодействия между падающим излучением и поверхностью ЭТ выражается в виде отдельной фазовой задержки exp{i*k*F(x)}, где k - волновое число, a F(x) - функциональная зависимость, выражающая форму профиля поверхности ЭТ, которая с помощью Фурье преобразования может быть выражена как
.
Через вычисления коэффициентов разложения Вn получено выражение для определения интенсивности отражаемого от трапециевидной решетки монохроматического излучения в дальней зоне для экстремальных точек - главных дифракционных максимумов.
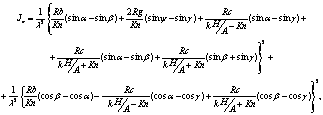де kH+KnB=α, kH-KnB=β, Kn(B+A)=γ, KnD=ψ, K=
, k=
, В, A, D, Н - параметры решетки.
Эта зависимость отличается от решения полученного в работе [5] для периодических МЭС, не учитывающего специфики ЭТ МЭС - наличие склонов травления и разных коэффициентов отражения от дна, вершин и склонов.
В ходе аддитивных и субтрактивных процессов коэффициент отражения изменяется, что приводит к изменению спектральных характеристик при неизменных геометрических характеристиках.
Свойства симметрии в дифракции Фраунгофера не нарушаются при изменении коэффициентов отражения, но при возникновении ассиметрии в профиле ЭТ эти свойства нарушаются.
При наклонном падении зондирующего излучения в плоскости параллельной штрихам решетки и совпадающей с нормалью к ее поверхности, можно добиться того, что индикатрисы рассеивания излучения в главные дифракционные максимумы старших порядков будут иметь достаточные величины малых осей эллипсоидов вращения, чтобы использовать из размеры в вычислениях шероховатости поверхности.
Используя вышеприведенную зависимость для моделирования дифракционного спектра, образованного при нормальном падении зондирующего монохроматического излучения на диэлектрическую тест-структуру с ЭТ субмикронного диапазона, был создан банк данных.
С помощью компьютерного моделирования были синтезированы виртуальные объекты, позволяющие изучать особенности дифракции на непрозрачных тест-структуры с трапециевидной топологией и разными коэффициентами отражения. При получении набора экспериментальных интенсивностей происходит оценивание каждой интенсивности In согласно принятой шкале оценок и из всего массива синтезированных спектров выбираются те, которые имеют наибольшее подобие экспериментальному дифракционному спектру. Затем шаг дробится и процедура повторяется снова.
Программная реализация разрабатываемой методики измерения включает в себя базу данных, математический аппарат для расчета интенсивности дифракционных спектров и синтеза спектров, имитирующих образ реального тест-объекта.
СПИСОК ЛИТЕРАТУРЫ
- Валиев К.А. Физика субмикронной литографии. - М.: Наука, 1990. - 528 с.
- Беклемишев Н.Н., Беневоленский С.Б., Истомина Н.Л. Повышение точности дифрактометрического метода измерения размеров элементов топологии микроэлектронных структур. - Микроэлектроника, 1998, т. 27, №6, с. 448-451
- Тудоа П.А., Быков В.А., Волк Ч.П. и др. Метрологическое обеспечение измерений длины в микрометровом и нанометровом диапазонах и их внедрение в микроэлектронику и нанотехнологию. Часть I. - Микросистемная техника, 2004, №1, с. 38-44
- Холопов Г.К. Математическая модель рассеивающих свойств диэлектрических поверхностей. - Оптический журнал, 2000, т. 67, вып. 10, с. 31-39.
- Волков В.В., Герасимов П.Л., Капаев В.В., Ларионов Ю.В. Оптические методы измерения размеров элементов топологии БИС и СБИС. - Микроэлектроника, 1980, т. 9, вып.6, с. 554-563