Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

7-2. МИР ДЕФОРМАЦИЙ.

Теория упругости [11] знает всего ПЯТЬ типов деформации тел: сжатие, растяжение, сдвиг, изгиб и кручение, которые известными преобразованиями не сводятся друг к другу. Вместе с этим, в механике [12] известны многочисленные наглядные примеры тесной взаимосвязи, сопутствия друг другу сжатия и растяжения (рис. 11), сдвига и изгиба (рис. 12), сдвига и кручения и т.п. Из этих примеров самоочевидна своеобразная иерархия такого сопутствия:

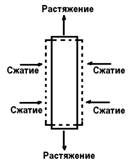
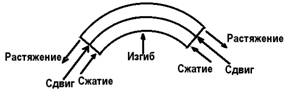
Рис. 11                                                                               Рис. 12

1. Сжатию сопутствует растяжение.

2. Сдвигу сопутствуют сжатие и растяжение.

3. Изгибу сопутствуют сжатие, растяжение и сдвиг.

4. Кручению сопутствуют сжатие, растяжение, сдвиг и изгиб.

Действительно, обозначая компоненты нормальных напряжений в некоторой точке деформируемой среды через , а тангенциальных через , можно записать известное выражение для тензора напряжений [7] из которого наглядно видно влияние всех компонент напряжений:

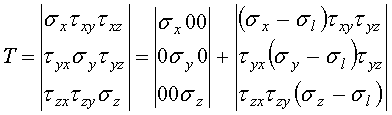.                 (6)

Как известно [13], уравнение поверхности нормальных напряжений  в некоторой точке деформированной среды в прямоугольной системе координат можно выразить:

                  (7)

В частных случаях [8] такая поверхность может принимать один из показанных на рис. 13 (сфера), рис. 14 (тор) и рис. 15 (скрученный тор) видов:

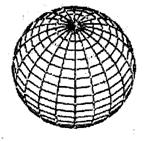
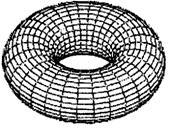
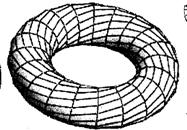
Рис. 13                                                 Рис. 14                                                 Рис. 15

Другими словами, очередные виды деформаций связаны с новыми возможностями, появлением новых свойств деформируемого объекта, как это свойственно процессу увеличения размерности мира [9]. Следовательно, мир деформаций мы вправе представить в качестве многомерного пространства, в котором «дополнительное» свойство представляет собой дополнительную способность данной деформации, как это показано на рис. 16. При этом, присваивая каждому новому виду деформации дополнительное направление, мы должны будем кручению «присвоить» все три измерения. На основании изложенного представляется обоснованной своеобразная иерархия деформаций:

1. Сжатие. 2. Растяжение. 3. Сдвиг. 4. Изгиб. 5. Кручение.

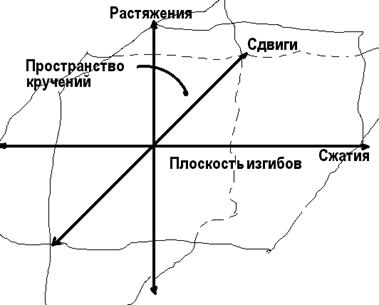
Рис. 16

В связи с изложенными соображениями здесь уместно вспомнить из теории упругости так называемые «УСЛОВИЯ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ» Сен-Венана [12], которые определяют непрерывность среды. Как это мы обнаружили в работе [9], главный принцип ТОПОЛОГИИ - НЕПРЕРЫВНОСТЬ является отражением главного свойства нашего МИРА - НЕПРЕРЫВНОСТИ его СУБСТАНЦИИ. Таким образом, количественное увеличение дополнительных направлений (свойств, способностей, возможностей...) приводит к появлению новых качественных признаков, величин, параметров...Сопоставляя этот наш атрибутивно - субстанциональный взгляд на категории размерности с известными эмпирическими положениями об объективности лишь двух видов материи (вещества и поля) и с отсутствием в природе «просто» движения в пустоте как смещения относительно «абсолютного» пространства, приходится признать, что для всех материальных объектов в виде полей или вещественных тел предполагается общая среда, в которой и локализованы все материальные объекты (тела и поля), взаимодействуя между собой по установленным законам.

История физики со времен Аристотеля многократно приходила к идее об эфире - некоей субстанции, в которой протекают все наблюдаемые нами процессы. Не повторяя здесь хронологию этих гипотез, отошлю читателя к авторам, уже
в XX веке выдвинувших свои подобные гипотезы, которые так и не стали продуктивными теориями, так как не смогли преодолеть известные противоречия гипотезы эфира. Отсылая читателя к полным текстам трудов упомянутых мыслителей, я здесь процитирую лишь по одной ключевой в данном направлении мысли каждого из упомянутых авторов:

«...Пространство - единство, в котором форма образована частицами, расположенными по поверхности объёма, вырезанного ими из пустоты, а содержание представляет собой густоты и частицы, заполняющие этот объём...» (См. [14], стр. 45 и далее).

«...Таким образом, по совокупности всех требований наилучшим образом свойствам микромира удовлетворяет газоподобная среда...» (См. [15], стр. 46 и далее).

«...классическая динамика и квантовая механика представляют собой две дополнительные процедуры атомной теории...» (См. [16], стр.18 и далее).

«...Таким образом, глобула - это элементарная единица макрообъёма газа и жидкости, в которой сочетается единство массы, энергии и пространства, а также, как увидим ниже, электрических зарядов...» (См. [17], стр.10 и далее).

С целью выяснения объективных причин тех систематических неудач многочисленных вариантов гипотез эфира мне придётся, учитывая мизерный тираж издания, процитировать себя из упомянутой статьи [9]: «В 1935 году Нильс Бор в работах по квантовой физике пришел к гносеологическому выводу, что явления в микромире представляются понятными на механическом уровне. В частности, его «планетарная» модель, построенная на механическом равновесии сил электрических между электронами на орбитах и протонами в ядре атома и центробежными силам инерции движения электронов по орбитам, дополненная квантовым принципом, оказалась не только понятной даже для неспециалистов, но и наиболее продуктивной в атомной физике. Несмотря на многочисленные дополнения и изменения этой модели за вековую историю развития атомной физики, она оказалась не только самой объективной, но весьма продуктивной моделью атома. Соответствие этому принципу Бора, например, в генетике для объяснения механизма наследственности в живых организмах путём материальных носителей - хромосом позволило удивительно просто и полно понять эти совсем немеханические процессы в биологии, послужило мощным импульсом в развитии нового направления в биологии - генетики и т. п. Оставляя читателя за воспоминаниями из истории науки многочисленных фактов торжества принципа Бора, здесь необходимо лишь подчеркнуть его универсальность, которую можно использовать в качестве критерия объективности: соответствие научного вывода принципу Бора свидетельствует об объективности этого вывода.».

7-3. ПОВЕДЕНИЕ В МИРЕ ДЕФОРМАЦИЙ:

Назовём ДЕФОНОМ окрестность деформированной среды вокруг ЛОКАЛЬНОЙ ДЕФОРМАЦИИ в точке О с указанными компонентами нормальных  и тангенциальных  напряжений, поверхности которых показаны выше на рис. 6 рис. 7 и рис. 8. Ясно, что субстанция в мире деформаций обладает физическими свойствами, на которые мы не имеем никаких оснований распространять традиционные в физике наши представления (о плотности, температуре, вязкости, упругости и т. п.), поэтому вынуждены здесь пока этот вопрос оставить открытым. Можно лишь предположить пока, что эти свойства близки к свойствам физического вакуума, примерные представления о которых мы имеем по результатам инструментальных исследований ближнего космического пространства: температура близка к абсолютному нулю, вязкость соответствует сверхтекучести при сверхнизких температурах и т. п. При этом из отмеченного выше свойства совместности деформаций (см. рис. 4 по п. 2) ясно, что плотность  субстанции в таком ДЕФОНЕ сжатия больше плотности  субстанции в его окрестности, что можно графически представить некоторой зависимостью , (8) где  от точки О, как это показано на рис. 17. Так как поведение таких ДЕФОНОВ определится направлениями указанных напряжений, то в этом вопросе должна быть полная определенность, обязывая нас рассмотреть его более подробно. Здесь уместно вспомнить, что понятие НАПРАВЛЕНИЯ в ГЕОМЕТРИИ определяется величиной УГЛА - величины, которая появляется лишь в двумерных мирах - поверхностях (радиан) и в трёхмерных мирах (стерадиан). При этом, если для если для однозначности величины плоского УГЛА необходимо указание его знака (правый - по часовой стрелке или левый - против часовой стрелки относительно заданного РЕПЕРА - линии), то для однозначности величины УГЛА пространственного ещё необходимо указание и его ориентации относительно поверхности (ВНУТРЕННИЙ или ВНЕШНИЙ), что непосредственно связано с радиусом кривизны соответствующей поверхности. Для иллюстрации отмеченного обстоятельства воспользуемся результатами топологических исследований векторных полей на поверхностях [18] и др. Представим себе простейший такой сфероидный ДЕФОН сжатия в окрестности точки О как на рис. 18, тогда на рис. 19 получим изображение векторных полей нормальных  (рис. 19-а) и тангенциальных  (рис. 19-б) компонент напряжения в смежной со сфероидом окрестности, которые по определению ортогональны друг другу (см. рис. 19). (рис. 89-а) и б) по [18]) Вместе с этим, два подобных ДЕФОНА, расположенные вблизи друг от друга, окажутся с противоположных сторон любой поверхности, которые всегда могут быть представлены замкнутыми в бесконечности по несобственной линии вокруг любого из ДЕФОНОВ, как это наглядно показано на рис. 20, на котором - след пограничной поверхности между окрестностями ДЕФОНОВ A и B, имеющих характеристики m и m¹ соответственно. Ясно, что радиус кривизны этой поверхности  для ДЕФОНОВ A и B будет иметь противоположные знаки. Из отмеченных обстоятельств сразу следует необходимость сближения двух соседних таких ДЕФОНОВ - СФЕРОИДОВ сжатия, что равнозначно притяжению, как это показано на рис. 20, оставляя пока открытым вопрос о величине такого тяготения.

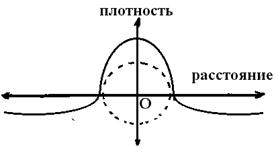
Рис. 17

Разумеется, направления полей нормальных  и тангенциальных  компонент напряжения в смежных с другими нашими простейшими ДЕФОНАМИ окрестностями, имеющих поверхности тороида (рис. 14) и скрученного тороида (рис.15) необходимо рассмотреть с этих позиций также подробно. Из одного того факта, что в отличие от односвязного сфероида тороид (см. рис. 14) является двухсвязным [18], сразу следует вывод об отсутствии центральной симметрии векторного поля нормальных  компонент напряжения, присущих сфероиду (см. рис. 18), приобретая в полярной плоскости, ортогональной экваториальной плоскости тороида, осевую симметрию, позволяя представить изменение векторного поля нормальных  компонент напряжения, опуская математические преобразования, проделанные автором ранее [19], как на рис. 21, на котором обозначены штриховыми линиями n и - n предельные уровни значений векторного поля нормальных  компонент напряжения. Из отмеченных обстоятельств снова следует вывод о необходимости сближения двух соседних таких ДЕФОНОВ-ТОРОИДОВ сжатия, что равнозначно притяжению, подобно притяжению ДЕФОНОВ-СФЕРОИДОВ на рис. 20, но величина такого тяготения ДЕФОНОВ-ТОРОИДОВ находится в зависимости не только от расстояния между ними, но и от относительной друг друга пространственной ориентации: в экваториальных плоскостях их взаимодействие подчиняется центральной симметрии, подобно взаимодействия ДЕФОНОВ - СФЕРОИДОВ
(см. рис. 20), а в полярной плоскости взаимодействие ДЕФОНОВ-ТОРОИДОВ сжатия подчиняется осевой симметрии, также здесь оставляя пока вопрос о величине такого тяготения открытым. При этом здесь важно отметить действие отмеченной особенности взаимодействия ДЕФОНОВ-ТОРОИДОВ в отличие взаимодействия ДЕФОНОВ - СФЕРОИДОВ лишь, как это ясно из графической зависимости на рис. 21, на расстояниях между ДЕФОНАМИ-ТОРОИДАМИ, сравнимыми с их собственными размерами.

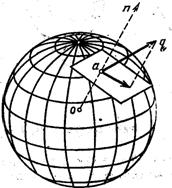
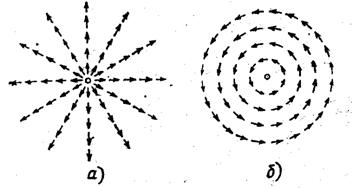
Рис. 18 (рис. 88 по [18])                                 Рис. 19 (рис. 89-а) и б) по [18])

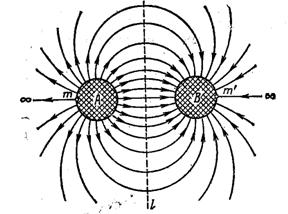
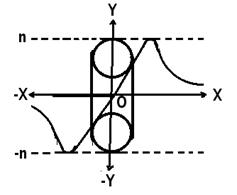
Рис. 20 (рис.186 по [18])                                            Рис. 21

Представить строение, но не механизм образования ДЕФОНА - скрученного ТОРОИДА (см. рис. 15) из ДЕФОНА-ТОРОИДА (см. рис. 14), ДЕФОНА - СКРУЧЕННОГО ТОРОИДА возможно по рис. 22-а), рис. 22-б) и рис.22-в), на которых показаны ДЕФОН- ТОРОИД (см. рис. 22-а) целый, ДЕФОН-ТОРОИД разрезан нормальной к его экватору плоскостью по А-В и торцы разреза развернуты относительно друг друга на 180⁰  (см. рис. 22-б), так что точки А₂ и В₁ поверхности ДЕФОНА-ТОРОИДА поменялись положением, то есть А₂ заняла положение В₁ , а В₁ заняла положение А₂, в результате образуя ДЕФОН-СКРУЧЕННЫЙ ТОРОИД (см. рис. 22-в).

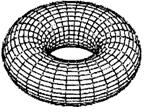
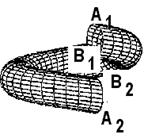
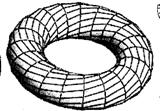
Рис. 22-а)                                              Рис. 22-б)                                            Рис. 22-в

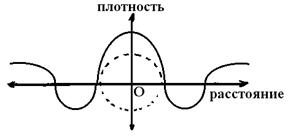
Рис. 23

В действительности образование ДЕФОНА-СКРУЧЕННОГО ТОРОИДА возможно представить как процесс движения окружности вокруг некоторой точки деформируемой среды по внешней оси - замкнутой траектории при вращении этой окружности относительно траектории движения центра этой окружности до замыкания траектории - являющейся осью ТОРОИДА. Как мы видели выше (см. рис. 16), деформации кручения сопутствуют все остальные виды деформации: и сжатие, и растяжение, и сдвиг, и изгиб. Поэтому особый практический интерес для нас представляет та зависимость  (8) плотности от расстояния внутри самого ДЕФОНА-СКРУЧЕННОГО ТОРОИДА и в его окрестностях, как это нами было установлено для ДЕФОНА - СФЕРОИДА (см. рис. 17), и также зависимость векторного поля нормальных  компонент напряжения в его окрестности, как это мы выше обнаружили для ДЕФОНА-ТОРОИДА
(см. рис. 14). В соответствии с отмеченными «УСЛОВИЯМИ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ» Сен-Венана [7] совершенно понятно, что при кручении ДЕФОНА-ТОРОИДА (см. рис. 15-б) его поверхностный слой испытывает растяжение, которое при необходимости можно даже вычислить, сравнив длины винтовой линии от А₁ до В₂ или от А₂ до В₁ с длиной соответствующего экватора тороида (см. рис. 15-а). Данное обстоятельство приводит к необходимости деформации растяжения в ближайшей СКРУЧЕННОМУ ДЕФОНУ-ТОРОИДУ (см. рис. 15-в) окрестности как рис. 23. Кроме того, рассматривая упругие напряжения на самой поверхности такого скрученного тороида, показанные на рис. 24, где линии напряжений на поверхности скрученного тороида между  и , также между  и , наглядно показанные на рис. 25, непременно приведут вследствие статической реакции к свертыванию этого СКРУЧЕННОГО ДЕФОНА-ТОРОИДА, которую в плане можно изобразить на рис. 26, а представить его реальный вид снизу на рис. 27 и реальный вид сбоку на рис. 28.

Другими словами, СКРУЧЕННЫЙ ДЕФОН-ТОРОИД образует своеобразную асимметричную СКОБУ, в окрестностях которой сопутствующие деформации образуют также асимметричную область, в пределах которой значения и направления нормальных  и тангенциальных  компонент напряжения отображают эту асимметричность окрестностей с различных сторон относительно СКОБЫ СКРУЧЕННОГО ДЕФОНА-ТОРОИДА.          

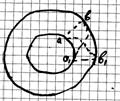
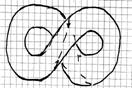
Рис. 24                                     Рис. 25.                                    Рис. 26

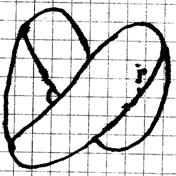
Рис. 27                                                 Рис. 28

СПИСОК ЛИТЕРАТУРЫ

1. Вайскопф В. Физика в двадцатом столетии. М., «Атомиздат», 1977.
2. Логунов А.А. «Релятивистская теория гравитации и новые представления о пространстве-времени // Вестник МГУ . Физика. Астрономия. т. 27, вып. 6, 1986, с.3 и далее.
3. Дирак П.А. Воспоминания о необычайной эпохе, пер. с англ. М., «Наука», 1990, с.178 и др.
4. Вертинский П.А. Финитность и сингулярность в понятии размерности пространства // VМНС, Красноярск, 2002.
5. Пригожин И.Р. и Стенгерс И. Порядок из хаоса. Новый диалог человека с природой. М., «Прогресс», 1986, стр. 275, 364 и др.
6. Мандельброт Б. Фрактальная геометрия природы. М.: ИКИ, 2002,стр.46, 144, 326.
7. Вертинский П.А. Естественнонаучные модели содержания категорий топологии // Сб.IX МНС, Красноярск,2006.
8. Вертинский П.А. Естественные модели размеров и размерностей в категориях топологии//Сб. X МНС, Красноярск, 2007,
9. Вертинский П.А. Естественные модели механизмов влияния природы процессов на размерности миров//Сб. XI МНС, Красноярск, 2008.
10. Вертинский П.А. К вопросу о полноте аксиоматики физических теорий // Вестник ИРО АН ВШ РФ№ 1(4) , Иркутск, 2004.
11. Седов Л.И. Механика сплошной среды. М., «Наука», 1976, т. I, стр. 63 и др., т. II, с. 317.
12. 12. Блох В.И. Теория упругости. Изд. ХГУ, Харьков, 1964, с. 201 и др.
13. Кривошапко С.Н., Иванов В.Н., Халаби С.М. Аналитические поверхности: материалы по геометрии 500 поверхностей и информация к расчёту на прочность тонких оболочек. - М.: Наука, 2006, с.97 и др.
14. Панин Д.М. Собрание сочинений в 4 т. Т. 2-й. Теория густот. - М.: «Радуга», 2001 г., с. 45.
15. Ацюковский В.А. Общая эфиродинамика. Моделирование структур вещества и полей на основе представлений о газонаполненном эфире. - М.: Энергоатомиздат, 1990 г. , с. 46 и др.
16. Гризинский М. О природе атома. // Поиск математических закономерностей Мироздания: физические идеи, подходы, концепции. Избранные труды ФПВ-2000, Новосибирск, НИИ им. С. Л. Соболева СО РАН, 2001, с. 9-16.
17. Базиев Д.Х. Основы единой теории физики. М., «Педагогика», 1994.
18. Болтянский В. Г. и Ефремович В. А. Наглядная топология. М., «Наука», 1982.
19. Вертинский П.А. Оптимизация электромеханических систем методами магнитодинамики // Сб. V «Сибресурс», Иркутск 2002