На основе известных дисперсионных кривых для свободных колебаний неоднородной жидкости определена ее неоднородность. В метриках пространств C, L1, L2 найдена погрешность отыскиваемой неоднородности в зависимости от точности входной информации (точности измеряемых длин внутренних волн в неоднородной жидкости и точности задания их частот).
В океанологическом приближении рассматривается задача о свободных колебаниях неоднородной жидкости [1]:
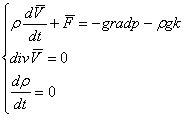(1)
где 
- вектор скорости в декартовой системе координат 
, связанной с поверхностью Земли, p - гидродинамическое давление, ρ - плотность жидкости,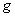 
- ускорение свободного падения, 
- сила Кориолиса, 
- вектор угловой скорости вращения Земли, k - единичный орт, направленный по оси z (противоположно силе тяжести).
Граничные условия запишутся следующим образом:
условия непротекания на дне имеют вид
,
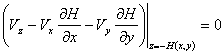кинематическое граничное условие:
,
здесь 
- возвышение свободной поверхности,
динамическое граничное условие записывается в следующем виде
.
В линейном приближении решение задачи (1) ищется в виде бегущих волн. В результате этого рассматриваемая задача сводится к следующей задаче для амплитудной функции вертикальной скорости W:
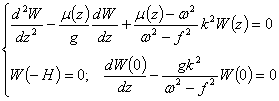(2)
В приближении Буссинеска с граничным условием типа «твердой крышки» (фильтрация поверхностных волн) в безразмерных величинах, после замены переменных
, 
, 
, 
, 
,
, 
,
задача сведена к следующей (опущено обозначение безразмерности «~», 
заменено на z):
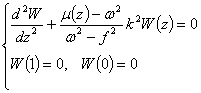(3)
Будем считать, что неоднородность жидкости задана по линейному закону 
и значения ω таковы, что существует точка поворота. То есть, пусть на отрезке [0,1] в одной точке z0 функция 
меняет знак, так что
, 
,
, 
.
Точка z0 называется точкой поворота, т.е. точка, в которой обращается в ноль переменный коэффициент в дифференциальном уравнении второго порядка системы (3).
Решение краевой задачи строим в явном виде:
, 
;
, 
;
, 
, 
.
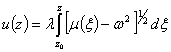Удовлетворяя граничным условиям, получаем частотное уравнение
.
Считая 
, заменим в этом уравнении функции Бесселя их асимптотическим представлением [2]
, при 
,
и учтем, что при больших z справедливо 
.
Частотное уравнение примет вид
.
Отсюда выводим
.
Так как , где , получим
, 
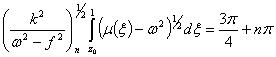Для линейного профиля скоростей интеграл вычисляется в явном виде, на основе которого при заданных значениях 
, 
, построены дисперсионные кривые.
Теперь ставится задача: считая, что известны значения ω и k с дисперсионных кривых, определить параметры неоднородности жидкости , .
Для их определения выписываем уравнение для двух пар (ω, k)
, ,
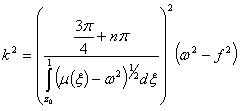что приводит к нелинейной системе для определения параметров , .
Нелинейность системы обуславливает неоднозначность определения параметров , . Для однозначности определения этих параметров выписывается «избыточное» число уравнений для «избыточных» пар чисел ω и k, и параметры , определяются как минимум функционала
.
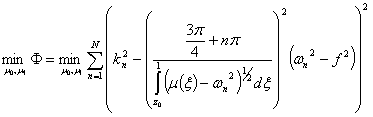Изучается точность восстановленной функции неоднородности жидкости:
в пространстве C
;
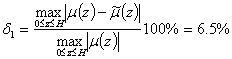в пространстве L1
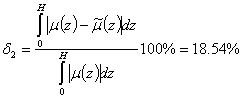
в пространстве L2
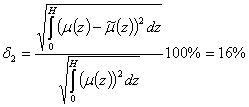
Здесь 
- восстановленная функция стратификации по найденным значениям параметров , , а функция 
- заданная стратификация жидкости.
При этом исследуется вопрос влияния на единственность и точность восстановления неоднородности жидкости тот факт, берутся ли пары чисел 
с одной дисперсионной кривой, или с разных. Также исследуется влияние близости между собой точек, взятых с дисперсионных кривых, на точность восстановления профиля стратификации.
СПИСОК ЛИТЕРАТУРЫ:
- Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. - Л.: Гидрометеоиздат, 1981. - 301 с.
- Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. - М.: Наука, 1971. - 1108 с.