Геометрия, предоставляя богатые возможности для постановки практических и проблемных задач, заданий, вовлекающих учащихся в экспериментальную деятельность, является эффективным средством формирования исследовательских умений.
В нашем исследовании мы исходили из предположения о том, что обучение геометрии в 7 - 9 классах с использованием специально разработанных дидактических средств для дифференцированного поэлементного формирования исследовательских умений и дифференциации учебных исследований по геометрии будет способствовать формированию у учащихся исследовательских умений, повышению уровня обученности по геометрии и развитию познавательного интереса к предмету.
В качестве основного дидактического средства для дифференцированного поэлементного формирования исследовательских умений использовались разноуровневые открытые задачи, направленные на развитие следующих структурных элементов названных выше умений: уметь формулировать цель работы, уметь анализировать условия заданной ситуации, уметь выдвигать и обосновывать гипотезы, уметь планировать решение проблемы, уметь анализировать результат.
|
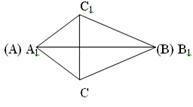
Дифференцированная карта-план урока ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ Вариант 5 (часть 1) 1. Верно ли следующее утверждение: "Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны"? Проверьте истинность данного утверждения экспериментально. С помощью транспортира и линейки изобразите треугольники АВС и А1В1С1 такие, что АВ=А1В1, ÐА=ÐА1, ÐВ=ÐВ1. Установить равенство треугольников можно двумя способами: 1) вырежьте один из треугольников и наложите его на другой (если треугольники совместятся наложением, то они равны); 2) с помощью транспортира и линейки измерьте соответственные элементы треугольников и сравните их. (В равных треугольниках соответственные элементы равны.) 2. Докажите утверждение 1 (второй признак равенства треугольников). Основная идея доказательства следующая: "Наложим треугольник АВС на треугольник А1В1С1 так, чтобы вершина А совместилась с вершиной А1, сторона АВ - с равной ей стороной А1В1, а вершины С и С1 оказались по одну сторону от прямой А1В1". (Продолжите рассуждения) ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ 3. Справедливо следующее утверждение (третий признак равенства треугольников): "Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны". Основная идея доказательства этого утверждения отражена на рис.1 (Прикладываем треугольник АВС к треугольнику А1В1С1 так, чтобы вершина А совместилась с вершиной А1, вершина В - с вершиной В1, а вершины С и С1 оказались по разные стороны от прямой А1В1). Докажите это утверждение.
______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ Какие еще возможны случаи взаимного расположения луча С1С и угла А1С1В1? _______________________________________________________________________________________________ ______________________________________________________________________________________
Как изменится доказательство, если луч С1С совпадет с одной из сторон угла А1С1В1? _______________________________________________________________________________________________ ______________________________________________________________________________________ Как изменится доказательство, если луч С1С проходит вне угла А1С1В1 ________________________________________________________________________________________________ 4. Возможно ли, чтобы в треугольниках АВС и МNК были справедливы неравенства АВ¹МN, ВС¹NК, СА¹КМ, а треугольники все же равны? Ответ проиллюстрируйте рисунком. |
Для дифференциации учебных исследований при обучении геометрии разработаны дифференцированные карты-планы уроков (ДКПУ) трех уровней сложности. С их помощью организуется самостоятельное изучение учащимися нового теоретического материала (первая часть ДКПУ) и применение полученных знаний при решении задач (вторая часть ДКПУ). При работе с новым теоретическим материалом повышение уровня сложности ДКПУ связано с увеличением степени самостоятельности ученика в открытии новых знаний и соотношением творческих и репродуктивных заданий. Приведем пример первой части ДКПУ третьего уровня сложности по теме "Второй и третий признаки равенства треугольников", которая предлагалась нами на уроках геометрии в седьмом классе.
Для проверки гипотезы исследования использовались следующие методы: анкетирование учащихся, проведение текущих самостоятельных и итоговых контрольных работ, предъявление учащимся исследовательской задачи после изучения каждой темы курса в качестве необязательного домашнего задания. Обработка полученных результатов с использованием статистических методов (в частности, метода биномиального критерия), построение соответствующих диаграмм позволили убедиться в справедливости выдвинутой нами гипотезы.