называется такое значение 
, что 
и 
.
В работе предлагается система задач, инициированных одной идеей, и её обобщение. Такое изложение может являться и иллюстрацией идеи развивающего обучения Д.Б. Эльконина - В.В. Давыдова, в которой утверждается: «для того, чтобы прийти к какому - либо обобщению при таком подходе, необходимо решить достаточно большое количество задач, постепенно выделяя «общие» для всех задач черты. Задача, поставленная перед учеником, может превратиться в учебную только в том случае, если ученик (самостоятельно или под руководством учителя) осуществляет переформулирование ее - вместо поиска частного способа решения он начинает искать обобщенный способ решения данного класса задач» [2].
Задача. Игроку предлагается купить жетоны по 2 рубля за каждый. Затем подбрасываются две игральных кости, а очки суммируются. За каждое выпавшее очко на каждый купленный жетон выплачивается по 3 рубля. Если жетонов больше, чем выпало очков, то за каждый оставшийся жетон выплачивают по 1 рублю. Сколько целесообразно купить жетонов?
Решение. Так как на двух костях может выпасть от двух до двенадцати очков, то покупать жетонов больше двенадцати и меньше двух нет смысла. Заполним таблицу для величины прибыли, соответствующей выпавшей сумме очков и количеству купленных жетонов.
Таблица 1. Величины прибыли, соответствующей выпавшей сумме очков и количеству купленных жетонов
|
Вероят-ность |
Кол-во жетонов j Сумма очков i |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1/36 |
2 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
-6 |
-7 |
-8 |
|
2/36 |
3 |
2 |
3 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
-6 |
|
3/36 |
4 |
2 |
3 |
4 |
2 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
|
4/36 |
5 |
2 |
3 |
4 |
5 |
4 |
3 |
2 |
1 |
0 |
-1 |
-2 |
|
5/36 |
6 |
2 |
3 |
4 |
5 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
6/36 |
7 |
2 |
3 |
4 |
5 |
6 |
7 |
6 |
5 |
4 |
3 |
2 |
|
5/36 |
8 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
7 |
6 |
5 |
4 |
|
4/36 |
9 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
8 |
7 |
6 |
|
3/36 |
10 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
9 |
8 |
|
2/36 |
11 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
10 |
|
1/36 |
12 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Математическое ожидание прибыли |
2 |
2,94 |
3,78 |
4,44 |
4,89 |
5,06 |
4,89 |
4,44 |
3,78 |
2,94 |
2 |
|
Наибольшее значение математическое ожидание прибыли игрока получается при покупке семи жетонов. Обратим внимание, что для случайной величины 
{сумма очков при подбрасывании двух игральных костей}, медиана 
равна 7, что совпадает с найденным оптимальным количеством жетонов.
Аналогичные примеры можно предложить, подбрасывая несколько игральных кубиков или монет, проводя повторные зависимые испытания или независимые испытания по схеме Бернулли.
Обобщенная задача. Игроку предлагается купить жетоны по a рублей за каждый. Затем проводится некоторый эксперимент, в результате которого игрок может набрать определенное количество очков. За каждое выпавшее очко на каждый купленный жетон выплачивается по a + h рублей 
. Если жетонов больше, чем выпало очков, то за каждый оставшийся жетон выплачивают по a - h рублей. Сколько нужно купить жетонов, чтобы выигрыш был максимальным?
Решение. Обозначим величину выигрыша при покупке j жетонов и выпадении i очков через 
.
По условию задачи,
Математическое ожидание 
прибыли игрока при покупке им j жетонов вычислим, используя найденные 
.
Из n чисел 
найдем максимальное значение 
, то есть такое, что
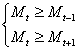
Поскольку 
, то
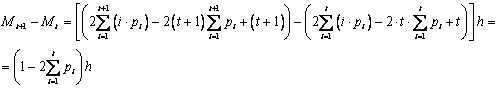
Следовательно,
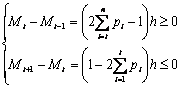или 
Откуда следует, что математическое ожидание прибыли игрока максимально, когда приобретаемое число жетонов совпадает с медианой первоначальной случайной величины X заданного испытания.
СПИСОК ЛИТЕРАТУРЫ
- Афанасьев В.В. Теория вероятностей в вопросах и задачах: Учебное пособие. Ярославль: Изд-во ЯГПУ им. К.Д.Ушинского, 2004. 250с.
- Смирнов С.А., Котова И.Б., Шиянов Е.Н. и др. Педагогика: педагогические теории, системы, технологии: Учебник для студ. высш. и сред. учеб. заведений. М.: Издательский центр «Академия», 1999. 512с.
Работа представлена на IV научную конференцию с международным участием «Стратегия естественнонаучного образования», 19- 26 февраля 2005г. Хургада (Египет). Поступила в редакцию 12.01.05 г.