Рассмотрим дискретно - импульсную систему управления, математическая модель которой описывается семейством уравнений
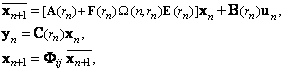(1)
где 
n-мерный вектор состояния объекта;
k-мерный вектор управления; 
s-мерный вектор выхода объекта; 
однородное дискретное состояние цепи Маркова, описывающее процесс смены режима объекта на множестве 
и матрицей вероятностей перехода 
от режима 
до режима 
;
известные матрицы соответствующих размеров; 
матрица неопределенных параметров, удовлетворяющая для каждого 
и 
неравенству
; (2)
постоянные матрицы, такие, что 
; эти матрицы описывают импульсное изменение вектора состояния объекта управления в момент смены режима на .
Будем предполагать, что вектор выхода 
и процесс смены режима доступны наблюдению.
Рассмотрим линейное управление со статической обратной связью по выходу объекта, синхронно переключаемой со сменой режима:
если (3)
такое, что для каждого фиксированного 
выражение (3) стабилизирует управление для детерминированной системы
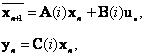
или, другими словами, такое, что матрица
является матрицей, собственные значения которой лежат в левой полуплоскости.
Матрица 
может быть получена при помощи известных методов решения проблем управления с детерминированной статической обратной связью по выходу.
Определим условия, которым должны удовлетворять управление (3), чтобы обеспечить стабилизацию в среднем квадратическом системы случайной структуры (1) для всех неопределенностей параметров объекта, удовлетворяющих (2). Такое управление назовем робастным стабилизирующим.
Для этого рассмотрим упрощенную систему
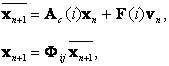(4)
где 
случайный вектор.
Если
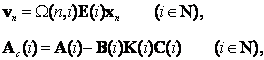(5)
то система (4) совпадает с исходной системой (1).
Тогда условия существования робастного стабилизирующего управления с обратной связью по состоянию для системы (4), задаются следующей теоремой.
Теорема. Пусть матрица 
положительно полуопределенная матрица,
некоторый положительный скаляр, для которого выполнено условие
Тогда, если положительно определенная матрица 
удовлетворяет неравенству
где 
то линейное управление со статической обратной связью по выходу объекта (3), является робастным стабилизирующим управлением.
Получили условие робастной стабилизации системы (4), которая при условии (5) переходит в систему (1).
СПИСОК ЛИТЕРАТУРЫ
- Pakshin P.V. Robust output feedback control of nonlinear systems with random jumps//Proceedings of 15th IFAC World Congress. Barcelona. Spain, 2002 p 1-6 (CD ROM).
- Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,2002.