Необходимость в исследовании математических моделей возникает, когда объект (явление) недоступен для изучения ввиду его опасности, отдален во времени и в пространстве от исследователя, а также, когда экспериментальные исследования сопряжены с большими материальными потерями и непредвиденными последствиями. Металлургические процессы как раз относятся к таким объектам. Наблюдается тенденция использования моделей на всех стадиях создания новых технологий и реализующих их агрегатов, а также при совершенствовании существующих процессов.
На рис.1 показаны типы моделей и направление их развития на указанных стадиях. Исследовательская модель I уровня (рис. 1) представляет собой самое простое математическое описание процесса (физического эффекта), позволяющее выполнить прогноз параметров процесса и лабораторной установки. На основе результатов экспериментальной проверки и изучения явления на установке модель I уровня развивается в модель II уровня, с помощью которой устанавливаются параметры технологии и конструкции опытно-промышленной установки. Далее в результате экспериментальных исследований на этой установке с помощью модели III уровня, полученной на основе модели II уровня, определяются параметры технологии и конструкции промышленного агрегата. На последней стадии создания системы управления технологическим процессом и агрегатом, а также разработки и уточнения технологии, обслуживания агрегата возникает необходимость в имитационной модели, автоматизированном рабочем месте технолога (АРМ инженера), и комплексе моделей для обучения, аттестации и тренинга обслуживающего персонала. Имитационные модели отличаются от исследовательских тем, что они дополнены алгоритмами управления основным физическим процессом и позволяют имитировать воздействие различных методов управления на этот процесс.
Только при таком сочетании теории и экспериментов (рис.1) возможно свести к минимуму все затраты на освоение новых технологий и агрегатов.
Неоценима роль моделей в обучении. Например, в специальных дисциплинах (для специальности 110100 - «Металлургия черных металлов») все знания, полученные при освоении естественнонаучных и общепрофессиональных дисциплин интегрируются в теории металлургического процесса, осуществляемого на агрегате. Однако, в теории конкретного процесса, как правило, рассматриваются закономерности отдельных сторон процесса (подпроцессов). математическая модель позволяет изучать закономерности металлургического процесса на конкретном агрегате во всей сложности. При этом нет опасности разрушения лабораторной установки или аварии на промышленном агрегате. Обучаемым предоставляется возможность в динамике наблюдать то, что происходит внутри агрегата, и управлять процессом.
Процессы построения модели и моделирования тесно связаны между собой. Иногда даже говорят, что модель возникает в результате моделирования. Моделирование проводится в соответствии с определенной методологией, представляющей собой совокупность приемов и методов, которые связаны логикой научного исследования и получения достоверных знаний об объекте. Наиболее наглядно эту логику можно представить на примере создания модели и моделирования действующего детерминированного объекта в виде цепочки этапов работы:
- объект, проблема, цель, гипотеза, предмет, метод и задачи исследования,
- Физическое описание объекта и его формализация на основе системного подхода, формулировка допущений,
- Разработка математической модели (≡ математического описания),
- Разработка численной модели (≡ алгоритмов решения),
- Разработка компьютерной модели (≡ программы),
- Тестирование алгоритмов решения,
- Проведение экспериментов, проверка адекватности и адаптация,
- Выбор исходных данных,
- Изучение объекта и определение границ достоверности модели,
- Решение задач исследования.
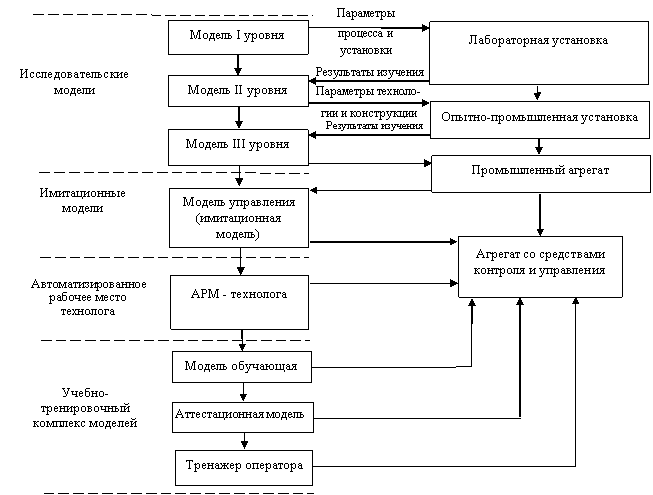
Рисунок 1. Схема развития и испол. моделей при создании новых технологий и реализующих их агрегатов
Количество перечисленных этапов сложилось в результате обобщения практики моделирования детерминированных процессов, а также материалов, приведенных в работах [1-4].
Следует отметить, что почти на каждом этапе возможен возврат к предыдущим этапам.
На кафедре металлургических технологий Института металлургии и химии ЧГУ работает научная школа, в которой обучается более 10 аспирантов - выпускников кафедры металлургических технологий, прикладной математики и других кафедр. В этой школе с помощью студентов - дипломников и аспирантов создаются математические модели детерминированных металлургических процессов.
Разработанные модели используются при изучении процессов и совершенствовании технологии на указанных агрегатах, а также в учебном процессе на кафедре.
СПИСОК ЛИТЕРАТУРЫ
- Яковлев Ю.Н. О математическом моделировании сталеплавильных процессов//Изв. АНСССР Металлы. 1991. №6. с. 197-201.
- Ясев А.Г. Некоторые вопросы использования математических моделей в металлургии//Сталь. 1999. №8. с. 94-97.
- Новосельцев В.Н. Математическое моделирование в век компьютеров//http://lgkb kazan.ru.
- Косарев В.А. Катасонов И.В. Современные комплексные системы обучения, тренинга и аттестации эксплуатационно-технологического персонала металлургических предприятий//Известия высших учебных заведений. Черная металлургия. 2002. №12. с. 58-61.
Работа представлена на III общероссийскую конференцию «Новейшие технологические решения и оборудование», г. Кисловодск, 19-21 апреля 2005 г. Поступила в редакцию 24.03.2005 г.



