В настоящее время компьютеры стали надежным, а иногда и единственным, средством решения научных, инженерно-технических, экономических, управленческих задач, в которых они традиционно применялись. Наряду с ними появились многочисленные нетрадиционные области приложения, такие как медицина, психология, социология, лингвистика, юриспруденция, искусство и многие другие. Это в большой степени способствовало созданию математических моделей для разнообразных задач, встречающихся в различных областях человеческой деятельности.
Пользуясь методами классической математики, можно непосредственно получить решение некоторых из этих задач в виде явных формул или аналитических зависимостей от известных функций, для которых составлены таблицы или номограммы, в виде сходящихся рядов и т.п. Однако существуют, по крайней мере, три соображения, которые делают необходимым применение компьютеров при математическом моделировании. Во-первых, возможность получения решения в явном виде для встречающихся на практике сложных задач является скорее счастливым исключением, чем правилом. Отсюда следует необходимость решать большинство перечисленных математических задач численно, с использованием компьютеров. Во-вторых, полученные методами классической математики аналитические решения часто имеют достаточно громоздкий вид и требуют использования компьютеров для получения конкретных числовых значений. В-третьих, для получения аналитических решений исходную техническую или экономическую задачу приходится упрощать, вводя различные предположения так, чтобы математическая модель допускала аналитическое решение. В этом случае численное решение полной задачи без упрощающих предположений не только позволяет полностью проанализировать исследуемый процесс, но и оценить влияние на него тех характерных параметров задачи, которыми мы пренебрегли при упрощения математической модели.
При реализации математических моделей на компьютерах существуют специфические особенности, некоторые из которых далее будут рассмотрены. Однако главную из них отметим сейчас. Классическая математика обычно рассматривает задачи с точки зрения доказательства существования и единственности решения и его характерных свойств. При этом, конечно. применяются и конструктивные алгоритмы, указывающие способ построения решения, но они часто имеют вид бесконечных процессов, дающих решение лишь е пределе. Поэтому возникла вычислительная математика которая занимается построением и анализом численных методов, позволяющих получить достаточно точное решение за конечное число шагов. допускающих возможность оценить сделанную ошибку и, быть может, указать приемы эффективного уменьшения этой ошибки.
В сложных задачах обычно неприменим в силу того, что границы области ответа становятся настолько большими, что говорить о значении ответа становится бессмысленным. другим способом оценки влияния округления является решение задачи с обычной и двойной точностью. Принято считать, что совпадающие в двух ответах разряды верны. Выполнив таким образом несколько вариантов типичных вычислений, далее можно вести остальные расчеты с обычной точностью, полагая, что я в них верно го же самое количество разрядов. Хотя опасности этого метода очевидны, тем не менее он используется на практике и обычно дает более точные результаты, чем метод области ответа.
Существуют статистические методы оценки влияния округления.
Без вывода приведем оценки погрешностей для отдельных арифметических операций над приближенными числами, для простоты обозначим
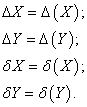
При сложения или вычитании чисел их абсолютные складываются
![]() (1)
(1)
для относительных погрешностей суммы или разности формулы имеют вид
![]() (2)
(2)
![]() (3)
(3)
Формулы для погрешностей при умножения и делении имеют вид
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Из (3) следует практически важный вывод о значительной потере точности при вычитании близких чисел, действительно, при ![]() относительная погрешность может быть сколь угодно большой.
относительная погрешность может быть сколь угодно большой.



