2250 лет тому назад Архимед теоретически установил величину и направление силового воздействия покоящейся жидкости на неподвижно расположенное в ней тело. Изучение открытого им закона входит в школьные и вузовские программы. К сожалению, и на сегодняшний день в учебниках при изложении доказательства закона Архимеда, уже современными математическими методами, плотность жидкости зачастую принимают постоянной [1, 2, 3,.4], что, в частности, не позволяет объяснить и рассчитать глубину плавания подводных тел и высоту подъема аэростатов.
Ниже предложен вариант обобщения закона Архимеда на случаи абсолютного и относительного неподвижного состояния тела в баротропной жидкости, находящейся в абсолютном или относительном равновесии при наличии силового поля тяжести, который может быть использован в вузовских лекционных курсах.
Абсолютное равновесие
При равновесии в жидкости развиваются только нормальные напряжения. Силовое воздействие тяжелой покоящейся жидкости на помещенное в ней неподвижное тело, не имеющее контактов с другими телами, создаваемое совокупностью давлений p на поверхности тела S, называют силой Архимеда, которая вычисляется по формуле
(1)
Силы давлений порождены полем силы тяжести, обладающим потенциалом
(2)
где 
- радиус вектор частицы жидкости, находящейся в этом поле. 
- вектор ускорения земного притяжения.
Из гидростатики известно, что поверхности равных давлений, равных плотностей и поверхности разрыва плотностей совпадают с поверхностями уровня силового поля 
. Поэтому можно плотность жидкости 
рассматривать как функцию потенциала U (
).
Для вычисления силы Архимеда мысленно извлечем из жидкости тело, сохраняя равновесие жидкости, а образовавшуюся пустоту, ограниченную поверхностью S, заполним покоящейся жидкостью с тем же распределение плотностей, что и в окружающей жидкости. Равновесие всей жидкости при этом сохранится, поля давлений вне и на поверхности S не изменятся. Будет находиться в равновесии и объем жидкости, ограниченный поверхностью S.
Воспользуемся теоремой о движении центра масс механической системы. В соответствии с ней центр масс движется как материальная точка, к которой приложены все внешние силы, действующие на систему, и в которой сосредоточена вся масса системы. Теорема, очевидно, справедлива и для равновесия системы. В рассматриваемом случае на выделенный объем жидкости действуют сила Архимеда (1) и параллельные силы тяжести частиц жидкости, заполнившей объем 
, ограниченный поверхностью S, которые обладают, как известно из теоретической механики, равнодействующей, определенной интегралом
(3)
Она приложена в центре масс С этой части жидкости. Векторная координата центра масс находится по формуле
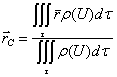(4)
Согласно теореме о движении центра масс, с учетом того, что рассматривается случай покоя, записываем равенство
(5)
Из этого уравнения следует формула, определяющая силу Архимеда
(6)
Так как сила Архимеда уравновешена одной силой - силой тяжести вытесненной жидкости, приложенной в точке с координатой 
, определяемой по формуле (4), то линия действия силы Архимеда обязательно проходит через эту точку С.
Формулы (6) и (4) составляют суть закона Архимеда.
Относительное равновесие
При относительном равновесии жидкости должны быть равными нулю относительные скорости и относительные ускорения частиц жидкости, а также ускорение Кориолиса, и оставаться постоянным вектор угловой скорости переносного движения 
. Следовательно, для относительного равновесия жидкости переносное ускорение может иметь только такое представление
(7)
где 
- ускорение полюса тела, положение которого в неподвижной системе координат определяется вектором 
, 
- векторное расстояние до оси вращения частицы жидкости, имеющей координату , вычисляемое по формуле 
.
С учетом формулы (7) уравнение относительного равновесия жидкости, находящейся в поле силы тяжести и инерционных сил, имеет вид
(8)
Потенциал Ф силового поля, соответствующего левой части уравнения (8), определяется по формуле
(9)
При этом 
.
На поверхностях уровня, описываемых уравнениями 
, сохраняются постоянными давления и плотности. Поверхности разрыва плотности также совпадают с соответствующими поверхностями уровня. Поэтому целесообразно рассматривать плотность, как функцию потенциала Ф ( 
.).
Определяем, пользуясь теоремой о движении центра масс, силовое воздействие жидкости, находящейся в относительном равновесном состоянии при поступательно-вращательном движении, на тело, удерживаемое в ней в относительном неподвижном состоянии. Воздействие жидкости на поверхность S тела при относительном равновесии такое же, как и на поверхность S жидкости, замещающей тело, если только сохраняется относительное равновесие всей жидкости. В исследуемом случае центр масс C* замещающего жидкого объема движется по окружности радиуса 
с ускорением 
под действием сил давлений, распределенных по поверхности S и системы параллельных сил 
, действующих на каждую частицу замещающей жидкости. Система этих сил имеет равнодействующую, определяемую таким интегралом
(10)
Она приложена в центре масс C*, положение которого находится по формуле
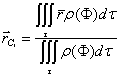(11)
Уравнение движения центра масс записывается так
(12)
Из этого уравнения следует формула для вычисления силы Архимеда, действующей со стороны жидкости на помещенное в нее тело при относительном равновесии
(13)
где 
.
Как видим, полная сила Архимеда при относительном равновесии приложена в центре масс заместившей тело жидкости C*, положение которого определяется по формуле (11), и равна сумме двух сил Архимеда: центростремительной силы Архимеда (первое слагаемое в формуле (13)), порожденной вращением жидкости, заместившей тело, и выталкивающей силы Архимеда, противоположно направленной сумме сил тяжести и инерции переносного поступательного движения жидкости, заместившей тело (слагаемое в квадратных скобках в формуле (13)).
Заметим, что положения центров тяжести жидкостей, заместивших тело, как и их массы, могут не совпадать в абсолютном и относительном равновесиях и могут зависть от расположения и ориентации тела, погруженного в жидкость.
Формулы (13) и (11) составляют суть закона Архимеда для воздействия баротропной жидкости, находящейся в относительном равновесии, на относительно неподвижно расположенное в ней тело. Их частными случаями являются формулы (6) и (4).
СПИСОК ЛИТЕРАТУРЫ
- Лойцянский Л.Г.Механика жидкости и газа..М., 1973. 817 с.
- Кочин Н.Е., Кибель И.Я., Розе Н.В. Теоретическая гидромеханика. М., 1963. Т. 1, 586 с.
- Валландер С.В. Лекции по гидроаэромеханике. Л., Издательство ЛГУ, 1978, 286 с.
- Batchelor G.K. An Introduction to Fluid Dinamics. Cambridge University. 2000. 631 pp.