Поведение теплоемкости реальных газов существенно отличается от той картины, которую рисуют классическая и квантовая теории. Особенно наглядно это видно на примере одноатомного газа. Согласно обеим этим теориям теплоемкость Cp одноатомного газа должна быть равна 2,5R при любой температуре и давлении. Однако, как следует из справочника [1], теплоемкость аргона, например, существенно зависит и от температуры и от давления. Так при 170К она оказывается разной при разном давлении. Удельная теплоемкость Cp при Р=10 бар равна 0,579 кДж/кгК; при 90 бар -
2,852 кДж/кгК, а при 200 бар - 1,276 кДж/кгК.
Максимальное значение молярной теплоемкости Cp достигает13,57R, а минимальное ни при каких давлениях не равно 2,5R. Такая же сложная зависимость теплоемкости аргона от температуры. При давлениях ниже 70-80 бар Cp с увеличением температуры уменьшается, а при давлениях больше 80 бар она сначала увеличивается, а затем уменьшается.
Все эти особенности поведения теплоемкости можно объяснить кластерной моделью газов. Если у молекул одноатомного газа нет вращательных и колебательных степеней свободы, то у их комплексов или кластеров они появляются. По этой причине при определении внутренней энергии газа следует учитывать не только поступательную энергию движения молекул, но и энергию связи кластеров, а также их вращательную и колебательную энергию. Причем, как оказалось, эти виды энергии следует учитывать по разному у малых и больших кластеров.
У малых кластеров вследствие небольшой энергии связи, порядка 100-150К, колебательная энергия в тех пределах изменения температуры, при которых кластеры существуют, меняется незначительно. Поэтому у малых кластеров колебательную энергию можно не учитывать. Здесь учитывается только энергия связи, а также энергия поступательного и вращательного движений.
Большие кластеры, вследствие их значительной массы, имеют малые скорости поступательного и вращательного движений.
Поэтому эти виды движений практически не участвуют в передаче энергии. Однако число колебательных степеней свободы очень большое. Колебательные движения отдельных атомов или молекул перестают быть независимыми.
Коллективные колебания молекул образуют стоячие волны (фононы). Число таких независимых стоячих волн 3 и поэтому энергия колебательных степеней свободы, приходящаяся на один моль, будет ![]() .
.
В кластерной модели газ считается идеальным в том смысле, что пренебрегается взаимодействием кластеров между собой. Взаимодействие молекул учитывается реакциями образования и распада кластеров и энергией связи молекул в кластере. По этой причине слагаемые в U, связанные с вириальными коэффициентами, опускаются. Однако при строгих расчетах их следует учитывать.
Учитывая выше сказанное, внутреннюю энергию кластеризованного газа можно записать в виде:
![]() (1)
(1)
где ![]() - температура, соответствующая минимуму энергии в потенциале Леннарда-Джонса,
- температура, соответствующая минимуму энергии в потенциале Леннарда-Джонса, ![]() - концентрация комплексов размерности g,
- концентрация комплексов размерности g, ![]() - средний размер кластера, v- число молей, подсчитанных по массе, т.е.
- средний размер кластера, v- число молей, подсчитанных по массе, т.е. ![]() , R-газовая постоянная, T- абсолютная температура.
, R-газовая постоянная, T- абсолютная температура.
В (1) первое слагаемое соответствует энергии связи комплексов, второе учитывает поступательную и вращательную энергию или колебательную энергию больших кластеров. Поскольку мономер одноатомного газа не имеет вращательных и колебательных степеней свободы, а димер имеет лишь две вращательных и одну колебательную степень свободы, то в (1) пришлось добавить последние два слагаемых, учитывающих этот фактор.
Так как теплоемкость CV определяется производной по T от U, то необходимо учитывать, что концентрация комплексов существенно зависит от температуры. Используя закон действующих масс, записывается следующее выражение для концентрации:
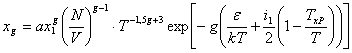 (2)
(2)
Учитывая это равенство можно найти ![]() и
и ![]() :
:
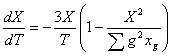 ; (3)
; (3)
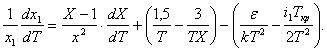 (4)
(4)
![]() (5)
(5)
- для сильно кластеризованного газа и
![]()
- для слабо кластеризованного газа.
Проделав все эти вычисления, для сильно кластеризованного газа получим следующее выражение для CV:
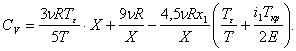 (6)
(6)
Поскольку газ сильно кластеризован, предельный переход к классической формуле невозможен.
Для слабо кластеризованного газа была получена другая формула:
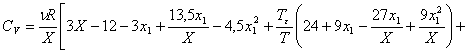 (7)
(7)
![]()
В этом случае предельный переход ![]() дает СV=1,5R.
дает СV=1,5R.
Полученные формулы, учитывая зависимость концентрации кластеров от температуры и давления, позволяют объяснить поведение теплоемкости реальных газов и ее зависимость от этих величин.
СПИСОК ЛИТЕРАТУРЫ
1. Вассерман А.А., Казавчинский Я.З., Рабинович В.А. Теплофизические свойства воздуха и его компонент. - М.: Наука, 1966.-376 с.



