Как известно, основным уравнением нерелятивистской квантовой механики является уравнение Шрёдингера, которое в одномерном случае имеет вид
![]() . (1)
. (1)
Уравнение (1) содержит гамильтониан
![]() , (2)
, (2)
который получается прибавлением потенциальной энергии U к оператору кинетической энергии
![]() . (3)
. (3)
При подстановке гамильтониана (2) в уравнение для стационарных состояний
![]() (4)
(4)
получается уравнение Шрёдингера (1). Как отмечено в [1], утверждение (2) «не является логическим следствием основных принципов квантовой механики, а должно рассматриваться как следствие опытных данных» ([1], с. 72).
Однако уравнение Шрёдингера (1) не всегда согласуется с опытными данными. Так, например, в случае линейного гармонического осциллятора (ЛГО), когда
![]() , (5)
, (5)
решение уравнение Шрёдингера (1) приводит к квантованию энергии
![]() ,
, ![]() (6)
(6)
Результат Шрёдингера (6) противоречит постулату Планка
![]() ,
, ![]() (7)
(7)
и, следовательно, законам равновесного теплового излучения (т.е. опытным данным). В основном состоянии равновесного теплового излучения плотность энергии согласно (6)
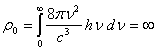 . (8)
. (8)
По мнению Бриллюэна, «этот результат неприемлем» ([2], с. 89). Трудность, связанная с результатом (8), отмечена также Фейнманом ([3], с. 18). Покажем, что это затруднение устраняется на основе обобщённого уравнения Шрёдингера, установленного в [4]. Учитывая, что в общем случае импульс может являться функцией координаты (например, в случае ЛГО:![]() ), получим
), получим
![]() . (9)
. (9)
Из (9) следует уравнение
![]() , (10)
, (10)
содержащее обобщённый оператор кинетической энергии
![]() . (11)
. (11)
С учётом (4) и (10) получается ОУШ
![]() , (12)
, (12)
установленное нами в [4] другим способом. Решением этого уравнения является
![]() . (13)
. (13)
Стандартное условие однозначности волновой функции приводит к равенству
![]() . (14)
. (14)
В случае ЛГО с потенциальной энергией (5)
![]() (15)
(15)
(см. напр., с.104 из [5]). Из (14) и (15) следует правило квантования (7), совпадающее с постулатом Планка. Таким образом, ОУШ (13) приводит к теоретическому обоснованию постулата Планка, с которого в 1900 г. началась история квантовой механики.
СПИСОК ЛИТЕРАТУРЫ
- Ландау Л.Д., Лифшиц Е.М. Квантовая механика. - М.: Наука, 1989. - 767 с.
- Бриллюэн Л. Квантовая статистика. - Киев, ГНТИУ, 1934.- 500 с.
- Фейнман Р. Статистическая механика.- М.: Мир, 1978. - 407 с.
- Свирский М.С., Свирская Л.М. Материалы VIII международной научно-практической конференции «Вузовское преподавание: проблемы и перспективы». - Челябинск, 2007. - с. 141.
- Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. - М. Наука, 1973.



