Вот как определяет сущность работы О.Д. Хвольсон [1, Стр.91-92] «Сила совершает работу, когда её точка приложения перемещается... ...следует отличать два случая производства работы: в первом сущность работы заключается в преодолевании внешнего сопротивления движению, которое совершается без увеличения скорости движения тела; во втором - работа обнаруживается увеличением скорости движения, к которому внешний мир относится индифферентно. На деле мы обыкновенно имеем соединение обоих случаев: сила ![]() преодолевает какие-либо сопротивления и в то же время меняет скорость движения тела».
преодолевает какие-либо сопротивления и в то же время меняет скорость движения тела».
Для вычисления работы постоянной силы предлагается формула:
![]() (1)
(1)
где S - перемещение тела под действием силы F, a - угол между направлениями силы и перемещения. При этом говорят [2], что «если сила перпендикулярна перемещению, то работа силы равна нулю. Если же, несмотря на действие силы, перемещение точки приложения силы не происходит, то сила никакой работы не совершает. Например, если какой-либо груз неподвижно висит на подвесе, то действующая на него сила тяжести не совершает работы».
В [2] также говорится: «Понятие работы как физической величины, введенное в механике, только до известной степени согласуется с представлением о работе в житейском смысле. Действительно, например, работа грузчика по подъёму тяжести расценивается тем больше, чем больше поднимаемый груз и чем на большую высоту он должен быть поднят. Однако с той же житейской точки зрения мы склонны называть «физической работой» всякую деятельность человека, при которой он совершает известные физические усилия. Но, согласно даваемому в механике определению, эта деятельность может и не сопровождаться работой. В известном мифе об Атланте, поддерживающем на своих плечах небесный свод, люди имели в виду усилия, необходимые для поддержания огромной тяжести, и расценивали эти усилия как колоссальную работу. Для механики же здесь нет работы, и мышцы Атланта могли бы быть попросту заменены прочной колонной».
Эти рассуждения напоминают известное высказывание И.В. Сталина: «Есть человек - есть проблема, нет человека - нет проблемы».
В учебнике физики для 10 класса [3, Стр.138] предлагается следующий выход из данной ситуации: «При неподвижном удержании человеком груза в поле тяжести Земли совершается работа и рука испытывает усталость, хотя видимое перемещение груза равно нулю. Причиной этого является то, что мышцы человека испытывают постоянные сокращения и растяжения, приводящие к микроскопическим перемещениям груза». Всё хорошо, вот только как рассчитать эти сокращения-растяжения?
Получается такая ситуация: человек пытается переместить шкаф на расстояние S, для чего он действует силой F в течение времени t, т.е. сообщает импульс силы ![]() . Если шкаф имеет небольшую массу и нет сил трения, то шкаф перемещается и значит, работа совершается. Но если шкаф большой массы и большие силы трения, то человек, действуя тем же импульсом силы, шкаф не перемещает, т.е. работа не совершается. Что-то тут не вяжется с так называемыми законами сохранения. Или взять пример, показанный на рис. 1. Если сила F направлена горизонтально (
. Если шкаф имеет небольшую массу и нет сил трения, то шкаф перемещается и значит, работа совершается. Но если шкаф большой массы и большие силы трения, то человек, действуя тем же импульсом силы, шкаф не перемещает, т.е. работа не совершается. Что-то тут не вяжется с так называемыми законами сохранения. Или взять пример, показанный на рис. 1. Если сила F направлена горизонтально (![]() ), то работа
), то работа ![]() , а если под углом a, то
, а если под углом a, то ![]() . Так как
. Так как ![]() , то, естественно, возникает вопрос, куда же исчезла энергия, равная разности работ (
, то, естественно, возникает вопрос, куда же исчезла энергия, равная разности работ (![]() )?
)?
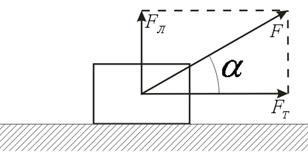
Рисунок 1. Сила F направлена горизонтально (![]() ), то работа
), то работа ![]() , а если под углом a, то
, а если под углом a, то ![]()
Приведем пример, показывающий, что работа совершается, если тело остаётся неподвижным. Возьмем электрическую цепь состоящую из источника тока, реостата и амперметра магнитоэлектрической системы. При полностью введенном реостате сила тока бесконечно мала и стрелка амперметра стоит на нуле. Начинаем постепенно двигать реохорд реостата. Стрелка амперметра начинает отклоняться, закручивая спиральные пружины прибора. Это совершает работу сила Ампера: сила взаимодействия рамки с током с магнитным полем. Если остановить реохорд, то установится постоянная сила тока и стрелка перестает двигаться. Говорят, что если тело неподвижно, то сила работы не совершает. Но амперметр, удерживая стрелку в том же положении, по прежнему потребляет энергию ![]() , где U - напряжение, подведенное к рамке амперметра,
, где U - напряжение, подведенное к рамке амперметра, ![]() - сила тока в рамке. Т.е. сила Ампера, удерживая стрелку, по прежнему совершает работу по удержанию пружин в закрученном состоянии.
- сила тока в рамке. Т.е. сила Ампера, удерживая стрелку, по прежнему совершает работу по удержанию пружин в закрученном состоянии.
Покажем, почему возникают подобные парадоксы. Вначале получим общепринятое выражение для работы. Рассмотрим работу разгона по горизонтальной гладкой поверхности первоначально покоящегося тела массы m за счет воздействия на него горизонтальной силой F в течение времени t. Этому случаю соответствует угол ![]() на рис.1. Запишем II закон Ньютона в виде
на рис.1. Запишем II закон Ньютона в виде ![]() . Умножим обе части равенства на пройденный путь S:
. Умножим обе части равенства на пройденный путь S:![]() . Поскольку
. Поскольку ![]() , то получим FS=mV2/2 или
, то получим FS=mV2/2 или ![]() . Отметим, что умножая обе части уравнения на S, мы тем самым отказываем в работе тем силам, которые не производят перемещение тела (
. Отметим, что умножая обе части уравнения на S, мы тем самым отказываем в работе тем силам, которые не производят перемещение тела (![]() ). Кроме того, если сила F действует под углом a к горизонту, мы тем самым отказываем в работе всей силе F, «разрешая» работу только её горизонтальной составляющей:
). Кроме того, если сила F действует под углом a к горизонту, мы тем самым отказываем в работе всей силе F, «разрешая» работу только её горизонтальной составляющей:![]() .
.
Проведем другой вывод формулы для работы. Запишем II закон Ньютона в дифференциальной форме
![]() (2)
(2)
Левая часть уравнения ![]() - элементарный импульс силы, а правая
- элементарный импульс силы, а правая ![]() - элементарный импульс тела (количество движения). Отметим, что правая часть уравнения может быть равна нулю, если тело остается неподвижным (
- элементарный импульс тела (количество движения). Отметим, что правая часть уравнения может быть равна нулю, если тело остается неподвижным ( ![]() ) или движется равномерно (
) или движется равномерно (![]() ), в то время как левая часть не равна нулю. Последний случай соответствует случаю равномерного движения, когда сила
), в то время как левая часть не равна нулю. Последний случай соответствует случаю равномерного движения, когда сила ![]() уравновешивает силу трения
уравновешивает силу трения ![]() .
.
Однако вернемся к нашей задаче о разгоне неподвижного тела. После интегрирования уравнения (2), получим ![]() , т.е. импульс силы равен импульсу (количеству движения), полученному телом. Возведем в квадрат, и разделив на
, т.е. импульс силы равен импульсу (количеству движения), полученному телом. Возведем в квадрат, и разделив на ![]() обе части равенства, получим
обе части равенства, получим
![]() или
или ![]() (3)
(3)
Таким образом мы получим другое выражение для вычисления работы
![]() (4)
(4)
где ![]() - это импульс силы. Это выражение не связано с путем S, пройденным телом за время t, поэтому оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным.
- это импульс силы. Это выражение не связано с путем S, пройденным телом за время t, поэтому оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным.
В случае, если сила F действует под углом a (рис.1), то её раскладываем на две составляющие: силу тяги ![]() и силу
и силу ![]() , которую назовем силой левитации, она стремится уменьшить силу тяжести. Если
, которую назовем силой левитации, она стремится уменьшить силу тяжести. Если ![]() будет равна
будет равна ![]() , то тело будет находиться в квазиневесомом состоянии (состояние левитации). Используя теорему Пифагора:
, то тело будет находиться в квазиневесомом состоянии (состояние левитации). Используя теорему Пифагора: ![]() , найдем работу силы F
, найдем работу силы F
![]() или
или ![]() (5)
(5)
Поскольку ![]() , а
, а ![]() , то работу силы тяги можно представить в общепринятом виде:
, то работу силы тяги можно представить в общепринятом виде:![]() .
.
Если сила левитации ![]() , то работа левитации будет равна
, то работа левитации будет равна
![]() (6)
(6)
Это как раз та работа, которую выполнял Атлант, удерживая на своих плечах небесный свод.
А теперь рассмотрим работу сил трения. Если сила трения является единственной силой, действующей по линии движения (например, автомобиль, двигавшийся по горизонтальной дороге со скоростью ![]() , выключил двигатель и стал тормозить), то работа силы трения будет равна разности кинетических энергий и может быть рассчитана по общепринятой формуле:
, выключил двигатель и стал тормозить), то работа силы трения будет равна разности кинетических энергий и может быть рассчитана по общепринятой формуле:
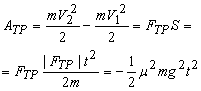 (7)
(7)
Однако, если тело движется по шероховатой горизонтальной поверхности с некоторой постоянной скоростью ![]() , то работу силы трения нельзя вычислять по общепринятой формуле
, то работу силы трения нельзя вычислять по общепринятой формуле ![]() , поскольку в данном случае движения надо рассматривать как движение свободного тела (
, поскольку в данном случае движения надо рассматривать как движение свободного тела (![]() ), т.е. как движение по инерции, и скорость V создает не сила
), т.е. как движение по инерции, и скорость V создает не сила ![]() , она была приобретена ранее. Например, тело двигалось по идеально гладкой поверхности с постоянной скоростью, и в тот момент, когда оно въезжает на шероховатую поверхность, включается сила тяги
, она была приобретена ранее. Например, тело двигалось по идеально гладкой поверхности с постоянной скоростью, и в тот момент, когда оно въезжает на шероховатую поверхность, включается сила тяги ![]() . В данном случае путь S не связан с действием силы
. В данном случае путь S не связан с действием силы ![]() . Если взять путь
. Если взять путь![]() м, то при скорости
м, то при скорости ![]() м/с время действия силы будет составлять
м/с время действия силы будет составлять ![]() с, при
с, при ![]() м/с время
м/с время ![]() с, при
с, при ![]() м/с время
м/с время ![]() с. Поскольку сила трения считают не зависящей от скорости, то, очевидно, на одном и том же отрезке пути
с. Поскольку сила трения считают не зависящей от скорости, то, очевидно, на одном и том же отрезке пути ![]() м сила
м сила ![]() совершит гораздо большую работу за 200 с, чем за 10 с, т.к. в первом случае импульс силы
совершит гораздо большую работу за 200 с, чем за 10 с, т.к. в первом случае импульс силы ![]() , а в последнем -
, а в последнем - ![]() . Т.е. в данном случае работу силы трения надо рассчитывать по формуле:
. Т.е. в данном случае работу силы трения надо рассчитывать по формуле:
![]() (8)
(8)
Обозначая «обычную» работу трения через ![]() и учитывая, что
и учитывая, что ![]() , формулу (8), опуская знак «минус», можно представить в виде
, формулу (8), опуская знак «минус», можно представить в виде
![]() (9)
(9)
Зависимость ![]() от
от ![]() , выраженных в долях
, выраженных в долях ![]() , показана на рис.2.
, показана на рис.2.
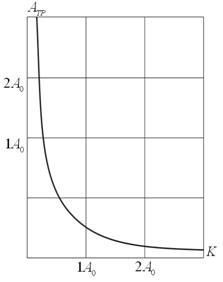
Рисунок 2. Зависимость ![]() от
от![]() , выраженных в долях
, выраженных в долях ![]()
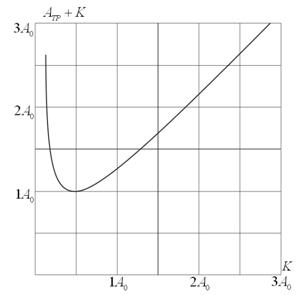
Рисунок 3. Зависимость суммы ( ![]() ) от величины
) от величины ![]() , выраженных так же в долях
, выраженных так же в долях![]()
На рис.3. показана зависимость суммы ( ![]() ) от величины
) от величины ![]() , выраженных так же в долях
, выраженных так же в долях![]() . Эта сумма имеет минимум, равный
. Эта сумма имеет минимум, равный ![]() при
при ![]() . То же самое относится и к случаю равномерного скольжения вниз по шероховатой наклонной плоскости (угол наклона
. То же самое относится и к случаю равномерного скольжения вниз по шероховатой наклонной плоскости (угол наклона ![]() ), когда сила трения равна скатывающей силе
), когда сила трения равна скатывающей силе ![]() или
или ![]() , т.е.
, т.е.![]() . В этом случае, чтобы тело равномерно скользило вниз, оно должно получить начальный импульс
. В этом случае, чтобы тело равномерно скользило вниз, оно должно получить начальный импульс ![]() . Тогда работа силы трения будет определяться не длиной наклонной плоскости S, а временем скольжения
. Тогда работа силы трения будет определяться не длиной наклонной плоскости S, а временем скольжения ![]() :
:
![]() (10)
(10)
Учитывая, что ![]() ,
,![]() , а
, а ![]() , опуская знак «минус», получим
, опуская знак «минус», получим
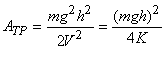 (11)
(11)
Зависимость ![]() от K совпадает с графиком (рис.2), только вместо
от K совпадает с графиком (рис.2), только вместо ![]() следует подставить (
следует подставить (![]() ), то же самое относится и к графику на рис. 3.
), то же самое относится и к графику на рис. 3.
СПИСОК ЛИТЕРАТУРЫ
- Хвольсон О.Д. Курс физики. Т. I. Р.С.Ф.С.Р. Госуд.Изд-во, Берлин, 1923.
- Элементарный учебник физики. Т. I. - М.: Наука, 1972.
- Касьянов В.А. Физика. 10 класс. Учебн.-М.: Дрофа, 2003.



