В качестве решения, например, может быть применён, например, метод нейросетевого анализа. При этом, важно правильно выбрать архитектуру и построить "обучение" сети. Данный метод является одним из приоритетных при условии, что n - достаточно велико. Тогда обучение сети можно осуществить автоматизированным методом и точность определения будет достаточно высока. Однако, при небольшом количестве рядов точность определения будет недостаточной, количество ложных срабатываний будет в разы больше чем верных.
Другим подходом к решению поставленной задачи может быть метод варьирования (полного перебора) и выявления влияния друг на друга при помощи методов приближённых вычислений. Однако все эти методы требуют достаточного большого количества операций, и при большом количестве вариантов время поиска будет велико. Причём будет расти не линейно, и не даже квадратично. Например, при количестве параметров m, количество проверяемых вариантов при глубине поиска в две переменных - m2+2*m4. При этом если параметр является переменной от 3 других параметров, то зависимость не будет найдена. Следовательно, метод варьирования будет эффективен только для рядов с небольшим количеством параметров.
Становится ясно, что способ нейросетевого анализа имеет жёсткие ограничения на количество рядов, а метод варьирования имеет жесткие ограничения на длину ряда. Необходим метод, который допустимо хорошо работал бы с любыми входными данными в рамках заданных ограничений. При этом время работы алгоритма должно быть линейным или сравнимо с линейным.
Рассмотрим задачу поиска искажений входные данные на примере матрицы чисел m*n, где m - количество параметров, а n - количество однородных (однотипных) рядов. К данным таблицы предъявляется два условия - первое состоит в том, что некоторые величины построчно коррелируют друг с другом или являются функцией других параметров, второе - что большинство чисел (более 95 % например) - корректные. Требуется отыскать точки (элементы) матрицы, в которых имеют место нелогичные возмущения. При этом правила зависимости (функции) одних параметров от других существуют, но неизвестны. Возможно решение одной из двух задач.
Первая задача, более простая, - отыскание точек случайных возмущений в матрице без выявления зависимостей параметров друг от друга. Вторая задача, комплексная, - нахождение зависимостей параметров друг от друга и отыскание точек случайных возмущений в матрице.
Предлагается использовать модифицированный метод варьирования. Его суть состоит в следующем - рассматриваем каждый столбец как параметр некой функции. Рекурсивно разбиваем все параметры по интервалам, и для каждого интервала формируем результирующий параметр. Причём результирующий параметр не может быть аргументом функции. Идём при помощи объединений от простейшей функции - функции одного аргумента. Если выявлено влияние одного параметра на другой, то исключаем один из них из дальнейшего просмотра, уменьшая количество параметров для дальнейшего просмотра. Найденные зависимости помещаем в стек, чтобы впоследствии начать рассмотрение с зависимостей с максимальным числом параметров.
Для определения зависимости параметров от результата используется следующий метод - представим данные каждого ряда как точку функции. Для матрицы рассматривается двухмерный вид - точка на плоскости. Тогда точки, которые выбиваются из графика функции и являются точками возмущения. Рассмотрим простейший пример:
Входные данные:
|
|
a |
b |
c |
|
1 |
1 |
5 |
5 |
|
2 |
2 |
10 |
8 |
|
3 |
7 |
35 |
5 |
|
4 |
3 |
15 |
8 |
|
5 |
6 |
30 |
5 |
|
6 |
9 |
45 |
11 |
|
7 |
5 |
25 |
8 |
|
8 |
4 |
15 |
9 |
|
9 |
11 |
55 |
3 |
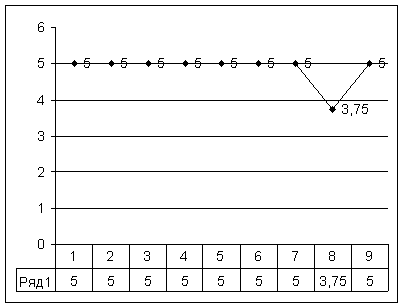
График 1. Линейная зависимость a от b
Необходимо выявить и исправить ошибку в переменной b в восьмом ряду. Построим линейную зависимость a от b.
Из графика 1 чётко видно возмущение в точке №8.
Для линейной зависимости поиск зависимостей не составляет сложности. Для нелинейных случаев необходимо уже применение методов отыскания новой точки функции по уже известным. Для этого добавляем информацию обо всех точках в информационную таблицу приближённой функции b= 
(a). Информация об ошибочных точках также попадает, но она не вносит сильного искажения, так как количество таких точек невелико, и вес каждой из них будет невелик. Далее производим поиск для каждой точки, при помощи, например, сплайн функций, далее вычисляем:
, и получаем приближённое значение для каждой точки b. Далее вычисляем коэффициент расхождения k: 
Далее, для каждой точки рассчитываем 
Если 
, то с достоверностью 
можно утверждать, что точка ошибочная.
Проведя анализ для всех точек всех рядов, получаем искомые точки за линейное время.
Работа представлена на научную конференцию с международным участием «Секция молодых ученых, студентов и специалистов», Тунис, 12-19 июня 2005 г. Поступила в редакцию 28.04.2005 г.