Для решения задач общей направленности и получения материалов с заданными свойствами наилучшим образом подходят аналитические решения, так как они в явном виде содержат основные физические свойства среды. Следует однако, отметить, что получение решений задач теплопроводности с помощью точных аналитических методов представляет большие математические трудности и состоит в необходимости решения многопараметрических трансцендентных уравнений, не имеющих решений в общем виде.
При исследовании критических режимов теплообмена рассматривается система уравнений движения и сохранения энергии. В произвольном призматическом канале при ламинарном течении жидкости в предположении, что теплофизические характеристики меняются незначительно и перенос теплоты вдоль направления движения за счет теплопроводности много меньше вынужденного после перехода к безразмерным параметрам систему уравнений удается свести к одному дифференциальному уравнению в частных производных:
(1)
где 
- безразмерные функции координат;
- безразмерная функция температуры; коэффициенты 
и 
характеризуют интенсивность тепловыделения от вязкого течения и от протекания химической реакции; коэффициент a является отношением энергии активации вязкого течения к энергии активации химической реакции;
- безразмерный коэффициент, связывающий температуру стенки трубы с энергией активации химической реакции; функция 
зависит от формы поперечного сеченья канала и от второго инварианта тензора скоростей деформации.
Для решения дифференциального уравнения (1) экспоненциальные функции, содержащие безразмерную функцию температуры , и она сама были разложены в ряды Тейлора. Приравняв соответствующие коэффициенты при различных степенях 
и 
для функций 
, 
, 
, 
, 
,
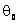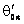полученные выражения после подстановки в уравнение (1) позволяют получить обыкновенное алгебраическое уравнение, которое было исследовано на существование и количество решений.
Работа представлена на научную конференцию с международным участием «Технологии 2005» , г. Анталия (Турция), 22-29 мая 2005 г. Поступила в редакцию 12.04.2005 г.