Круговорот вещества между органическим миром иатмосферой происходит чрезвычайно интенсивно. Огромную роль вэтом процессе играет океан, аименно живущие внем животные ирастения, поглощение ивыделение газов приих жизни исмерти (разложении). Рассмотрим частную проблему круговорота углерода икислорода- модель Костицына. Вэтих уравнениях мыпренебрежем промышленной деятельностью человечества. Прежде всего, очень трудно представить ееколичественно, и, кроме того, ею, безусловно, можно пренебречь, пока речь идет овековых идаже многовековых периодах, ане отекущих событиях. Введем обозначения: х- масса свободного атмосферного кислорода; у- общая масса углекислоты ватмосфере ив океане; v- общая масса кислорода иуглерода врастениях; и- ихобщая масса вживотных; s- ихобщая масса востатках растений иживотных. Составим систему дифференциальных уравнений, гдекаждая переменная дифференцируется повремени. а13-коэффициент расхода кислорода надыхание животных; а14-коэффициент расхода кислорода надыхание растений; а41-коэффициент освобождения кислорода впроцессе питания растений; а32;a42-коэффициенты освобождения животными ирастениями углерода впроцессе дыхания иразложения живой материи; а35- коэффициент процесса разложения животных; а45- коэффициент процесса разложения растений; a24- коэффициент усваивания углекислого газа растениями.
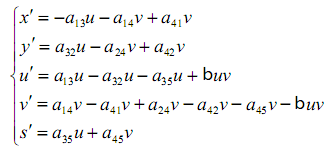
Согласно уравнению (1) атмосферный кислород расходуется надыхание животных (-а13u) идыхание растений (-а14v) иосвобождается впроцессе питания растений (+а41v). Уравнение (2) показывает, чтоатмосфера получает углерод, освобожденный растениями иживотными впроцессе дыхания иразложения живой материи (а32и, a42v) ичто растения усваивают углекислый газ(-a24v). Вуравнении (3) члены (+а13u) и(-а32u) описывают соответственно усвоение иотдачу газов животными ватмосферу; член βuvотражает тотфакт, чтоживотные питаются растениями, причем этот процесс описывается всоответствии стак называемым «принципом встреч» между поедающими ипоедаемыми; член -а35и описывает обогащение почвы врезультате разложения трупов животных. Чтокасается структуры, тоуравнения (4) и(5) неотличаются отпредыдущих. Приведем уравнения (3), (4) кболее простому виду:
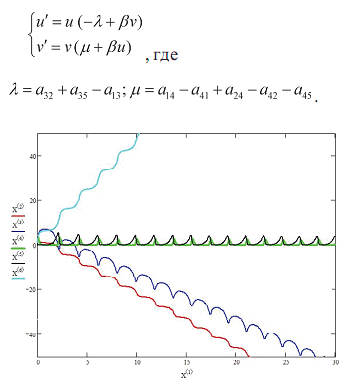
Исходя изэтих уравнений λ> 0, таккак вотсутствие растений животные немогли бысуществовать, атак какотсутствие животных повлекло быускоренное развитие растений, тоμ > 0. Построим графики функций впрограмме MathCAD спомощью метода фиксированного шага Рунге-Кутта. Дляэтого возьмем частный случай ипримем следующие условия: 1) растения больше усваивают углекислого газа, чемвыделяют, тоесть a24-a42 > 0; 2) растения больше усваивают кислорода; чемвыделяют, т. е. а14 - а41 > 0; 3) животные больше рассеивают вещества, чемприобретают, усваивая кислород, а35> а13; 4) a24 - a42 > а45 > а14 - а41 количество газа припроцессе усвоения ивыделения растениями углекислоты больше, чемтребуется наразложение растений ибольше, чемколичество газа припроцессе усвоения ивыделения растениями кислорода. Каквидно награфике, запас обоих газов (О2- красная, СО2- синяя) современем будет уменьшаться, аобщая масса кислорода иуглерода (голубая) востатках растений иживотных увеличиваться, аколичество кислорода иуглерода врастениях иживотных (зеленая ичерная) неизменяется.



