В настоящее время в России для определения тяжести ХСН, наряду с традиционной классификацией Василенко-Стражеско (1935г.), используют Нью-йоркскую классификацию ХСН, характеризующею функциональное состояние пациентов. Для объективной оценки состояния больного проводится 6-минутный тест ходьбы (определяют расстояние, пройденное пациентом за 6 минут и устанавливают функциональный класс ХСН).
Несмотря, на простоту и доступность 6-минутного теста, он имеет ограничения и недостатки. Так, у ряда больных из-за сопутствующих патологий, например, заболевания суставов нижних конечностей или у постельных больных установить функциональный класс (ФК) ХСН вообще невозможно. С другой стороны, расстояние, пройденное больным, зависит не только от состояния сердечно-сосудистой системы, но и от индивидуальных особенностей: психологических реакций, волевых качеств, мотивации лечащим врачом в необходимости такого тестирования. Перечисленные особенности приводят к неизбежным погрешностям при экспериментальном тестировании, что в свою очередь приводит к ошибкам при определении ФК ХСН больных.
Целью работы является статистическое моделирование взаимосвязи результатов 6-минутного теста и клинических проявлений сердечной недостаточности для достоверного предсказания результатов теста по известным значениям показателей сердечной недостаточности.
В исследования включены 350 пациентов ишемической болезнью сердца (ИБС) с ХСН I-IV ФК в возрасте от 39 до 75 лет (средний возраст 58,3). В группу не входили больные с прогрессирующей стенокардией, сахарным диабетом 1 типа, артериальной гипертонией III степени, инсультом, поражением суставов нижних конечностей. Средняя продолжительность ИБС - 7,8 лет. Больные наблюдались в течение 3-х лет на фоне стандартной терапии, включающей обязательный прием больными ß-блокаторов (метопролола сукцината) и ингибиторов ангиотензинпревращающего фермента (эналаприла). Назначение препаратов других групп определялось тяжестью ХСН и функциональным классом стенокардии напряжения.
Обследование больных проводили в 5 этапов: до начала лечения - этап 1, соответственно через полгода - этап 2, 1 год - этап 3 , 2 года - этап 4, 3 года - этап 5. На этапе отбора и на всех этапах 3-х летнего наблюдения осуществляли: оценку клинических проявлений ХСН - слабости (сл), одышки (од), утомляемости; измерение артериального давления (АДд), определение показателей центральной гемодинамики: конечного диастолического размера (КДР), конечного систолического размера левого желудочка (КСР), размера левого предсердия (ЛП) с использованием аппарата "Sequoia" (фирма "Acuson",США), показателей 6-минутного теста.
Показатели слабость и одышка являются качественными переменными, принимающими значения - нет, слабая, умеренная, выраженная, сильно выраженная. Остальные показатели - количественные. Статистическое моделирование и обработка результатов исследований проводилась с использованием лицензионной версии программы Statistica 6. 1.
Анализ законов распределения количественных показателей ХСН показал их несоответствие нормальному закону, поэтому в работе были использованы методы непараметрической статистики. В состав приведенных выше показателей входят качественные величины слабость, одышка, которые можем считать порядковыми. Закон распределения количественных величин не является нормальным. Поэтому для оценки характера взаимосвязи между слабостью, одышкой, КСР, КДР, ЛП, АДд и результатами 6-минутного теста использовали коэффициент корреляции тау Кендала - r [4]. Для всех этапов наблюдения установлена статистически значимая связь между вышеперечисленными параметрами: на 1 этапе rсл = -0,677, rод= -0,739, rКСР= -0,489, rКДР= -0,536, rЛП= -0,466, rАДд= -0,22; на 2 этапе rсл = -0,679, rод= -0,732, rКСР= -0,481, rКДР= -0,527, rЛП= -0,366, rАДд= -0,139; на 3 этапе rсл = -0,665, rод= -0,747, rКСР= -0,565, rКДР= -0,434, rЛП= -0,465, rАДд= -0,28; на 4 этапе rсл = -0,585, rод= -0,752, rКСР= -0,532, rКДР= -0,556, rЛП= -0,484, rАДд= -0,378; на 5 этапе rсл = -0,566, rод= -0,727, rКСР= -0,528, rКДР= -0,706, rЛП= -0,611, rАДд= -0,352.
Корреляционный анализ выявил следующие закономерности. Все корреляции отрицательные, т.е. увеличение любого показателя ведет к уменьшению показателя 6-минутного теста; все корреляции статистически значимы (верна гипотеза о том, что они не равны нулю) при уровне значимости 0,05. В процессе лечения (с увеличением продолжительности заболевания) коэффициенты корреляции изменяются незначительно. Существует зависимость, близкая к сильной между одышкой и количеством пройденных метров. Существует умеренная зависимость между количеством пройденных метров и наличием слабости, КДР, КСР левого желудочка, размером ЛП.
Коэффициент корреляции характеризует направление и силу линейной зависимости между величинами, но не показывает вида зависимости. Воспользуемся линейным множественным регрессионным анализом для построения статистической модели линейной зависимости 6-минутной пробы от рассматриваемых показателей сердечно-сосудистой недостаточности. Ниже приведены уравнения линейной множественной регрессии для этапов 1-5.
6мин.пр.1 = 1133,52 - 28,08·сл.1 - 48,1·од.1 - 61,39·КДР1 - 31,73·ЛР1 - 1,68·АДд1 (1)
6мин.пр.2 = 1099,02 - 34,34·сл.2 - 48,94·од.2 - 60,26·КДР2 - 19,87·ЛР2 - 1,99·АДд2 (2)
6мин.пр.3 = 1021,37 - 31,44·сл.3 - 54,39·од.3 - 34,24·КДР3 - 28,47·ЛР3 - 1,62·АДд3 (3)
6мин.пр.4 = 1115,70 - 37,06·сл.4 - 48,87·од.4 - 60,81·КДР4 - 34,39·ЛР4 - 1,24·АДд4 (4)
6мин.пр.5 = 1257,11 - 25,22·сл.5 - 46,80·од.5 - 75,45·КДР5 - 44,49·ЛР5 - 1,45·АДд5 (5)
Коэффициенты уравнения регрессии при КСР статистически незначимы (верна гипотеза о равенстве 0) для всех этапов, поэтому этот показатель отсутствует в уравнениях.
Количественной оценкой адекватности уравнения регрессии моделируемому процессу является показатель детерминации R2, который принимает значения от 0 до 1. Чем ближе R2 к 1, тем лучше регрессия объясняет зависимость в данных. Для этапов 1-5 R2 приняли соответственно значения 0,98; 0,95; 0,93; 0,96; 0,96. Показателем адекватности уравнения регрессии также является статистика Дарбина-Уотсона d и сериальная корреляция sr, которые характеризуют устойчивость коэффициентов уравнения. Для этапов 1-5 эти параметры приняли соответственно значения d = 1,94, 2,03, 1,86, 1,64, 1,96; sr = 0,025, -0,019, 0,048, 0,107, -0,003. Малые значения статистики d при малой сериальной корреляции sr свидетельствуют о независимости наблюдений, следовательно, можно говорить об устойчивости, а значит и об адекватности уравнений регрессии.
Одним из условий корректного применения регрессионного анализа является соответствие закона распределения остатков (разница между значением переменной, вычисленной по уравнению и полученной в результате тестирования) нормальному закону [5]. На рисунке 1 изображена гистограмма остатков (для этапа 1), из которой видно, что остатки имеют распределение «близкое» к нормальному. Соответствие распределения остатков нормальному закону является еще одним свидетельством адекватности построенных уравнений.
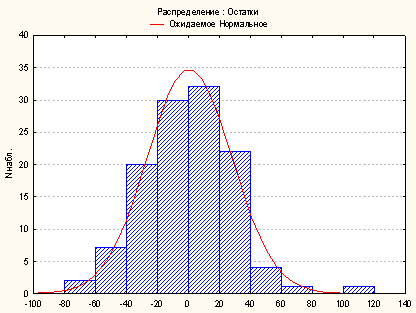
Рисунок 1. Гистограмма остатков
Если больной не наблюдался в лечебном учреждении или наблюдения не носили систематический характер можно воспользоваться общим уравнением регрессии:
6мин.пр. = 1125,28 - 24,49·сл. - 47,75·отд.- 35,7·ЛР - 1,47·АД.
При построении уравнения использованы средние величин по всем периодам наблюдения. Для значения 6-минутной пробы, КСР, КДР, ЛР, АДд оценкой среднего является среднее арифметическое. Для слабости, одышки оценкой среднего является медиана, так как можно считать, что эти величины измерены в порядковой шкале. Параметры модели имеют следующие значения: R2 = 0,94; d = 1,93; sr = 0,002, что также свидетельствует об адекватности модели.
Для экспериментальной проверки эффективности и адекватности полученных моделей на группе из 135 больных проведено сопоставление результатов 6-минутной пробы, полученных традиционным - экспериментальным способом и рассчитанных по статистическим моделям. Средний процент ошибки для этапов 1-5 составил соответственно 7,8%, 4,5%, 5,8%, 5,3%, 6,4%. Если учесть недостатки экспериментального тестирования, о которых говорилось ранее, данные погрешности незначительны.
Таким образом, приведенные результаты статистического моделирования, показывают, что в случаях, когда по каким либо причинам нет возможности провести 6-минутный тест, но известны клинические показатели состояния сердечно-сосудистой системы, для определения принадлежности больного к функциональному классу можно воспользоваться соответствующим уравнением множественной регрессии.
Такой способ оценки состояния больных ХСН является более достоверным по сравнению с экспериментальным, так как не зависит от человеческого фактора - психо-эмоциональных состояний участников тестирования - больного и врача. Может использоваться в качестве дополнительного (уточняющего) метода к экспериментальному тестированию, а для группы больных, которые не могут пройти экспериментальное тестирование - в качестве основного.
СПИСОК ЛИТЕРАТУРЫ
- Беленков, Агеев, В.Ю. Мареев. Знакомьтесь: диастолическая сердечная недостаточность. //Сердечная недостаточность. - 2000. - Т. 1. .№2. С.2-12.
- Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. М.: Медиа Сфера, 2003.
- Clealand F. Лекция по сердечной недостаточности. Под редакцией G.F.Clealand. Эпидемиология к патофизиологии сердечной недостаточности. Вступительное слово. G.F. Clealand. Научно-исследовательский центр Julius. Академическая книга. 2000.
- HCAAC //European Heart Journal, 2001.Vol.17.P.1-115.
- STATISTICA (Версия 6.1). Электронное руководство.



