Уравнение диссипации имеет вид:
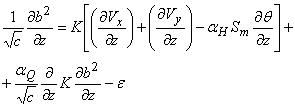, (1)
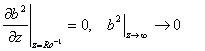
где b2 - величина, пропорциональная средней кинетической энергии турбулентности, K- коэффициент турбулентной диффузии, Vx,Vy - горизонтальные составляющие скорости движения воздушных масс, с, aH, aQ - безразмерные константы, Sm - амплитуда колебаний параметра температурной стратификации, e - средняя скорость диссипации, q - потенциальная температура, Ro - число Россби.
Решением уравнения (1) является функция b2. Для ее нахождения необходимо знать параметры пограничного слоя: скорости рассеяния примеси, потенциальную температуру и коэффициент турбулентной диффузии в исследуемой области.
Обозначим искомую функцию 
, учитывая что 
и 
, получим 
,
. Для удобства представим параметры Vx,Vy,q в виде функции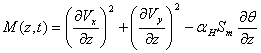 
и умножим обе части на 
. Используя новые обозначения, запишем (1) в следующем виде:
(2).
Искомую функцию n представим в виде суммы двух функций n=j+y, первая из которых определяет функцию n внутри исследуемой области, а вторая на ее границе:
, →
,
, 
,
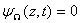где 
, 
,
z1,z2 - нижняя и верхняя границы исследуемой области.
Уравнение (2) примет вид:
(3).
Искомую функцию на границе G представим в виде:
.
В соответствии с принципом взвешенной невязки, выберем систему весовых функций wl (l=1..n), определенных в области W, таких, что:
,
и перепишем уравнение (3), используя выбранные базисные и весовые функции:
(4),
или в векторном виде:
,
где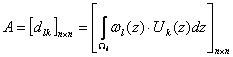 
,
,
,
,
,
.
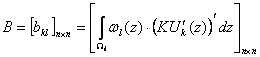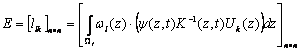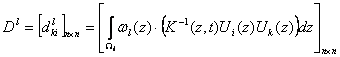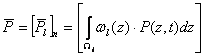Используя схему Кранка-Николсона, представим (4) в разностной форме:
.
В результате несложных преобразований получим рекуррентную формулу:
,
где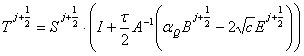 
, 
.
Используя формулу (6) мы определяем весовые коэффициенты при заданном базисе, и получаем возможность вычислить искомую кинетическую энергию системы.
СПИСОК ЛИТЕРАТУРЫ
- Наац И.Э., Семенчин Е.А. Математическое моделирование динамики пограничного слоя атмосферы в задачах мониторинга окружающей среды, Ставрополь, 1995 г.