Так как почти все факторы, формирующие микроклимат, непрерывно изменяются во времени, тепловое равновесие даже в помещениях с автоматически регулируемыми отопительно-вентиляционными приборами никогда не достигается. Поэтому стабильность внутренней температуры может рассматриваться только как результат взаимно уравновешивающегося воздействия очень большого числа динамических элементарных процессов.

Регрессионная модель микроклимата.

При планировании эксперимента по исследованию микроклимата в качестве параметров оптимизации были назначены три главные характеристики тепло-влажностного и воздушного режимов помещения: температура T, относительная влажность j и подвижность воздуха V.

Функциональная связь между рассматриваемым климатическим параметром y и пространственно-временными координатами определялась в виде полинома второй степени:

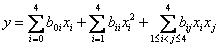.   (1)

Регрессионные коэффициенты

 при  при  при  вычисляются по методу наименьших квадратов из системы нормальных уравнений

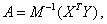      (2)

где матрица неизвестных  матрица выходных параметров испытаний  Общее число опытов N зависит от типа факторного плана, по которому проводится эксперимент. Информационная матрица Фишера  строится с помощью матрицы условий

Условия проведения опытов  организуются по одному из симметричных центральных планов второго порядка - рототабельному композиционному плану РКП или D-оптимальному четырехфакторному плану типа Бокса B₄ |2, 3]. РКП строится униформным с величиной безразмерного момента матрицы планирования l₃ = 0,8705. Управляемые факторы кодируются на пяти уров­нях, звездное плечо a == 2, общее число опытов N = 31. ядро плана состоит из 16 точек, количество дублирующих опытов в центре n₀ = 7.

При исследованиях по плану B₄ входные параметры кодируются на трех уровнях, N = 24, число звездных точек с плечом a = 1 составляет п_a = 8.

Элементы стандартной матрицы С =  находят в каталоге планов эксперимента для факторных и полиномиальных моделей.

После проведения натурных экспериментов на основе полученного стати­стического материала во всех помещениях здания по формулам (2) на ЭВМ рассчитывают значения регрессионных коэффициентов функции отклика (1) для каждого из параметров оптимизации t, j и v.

Проверка статистической значимости полученных коэффициентов осуществляется с помощью доверительных интервалов. Исключаются из модели (1) без пересчета статистически незначимые оценки при исключении одного из значений 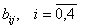требуется пе­ресчитывать остальные коэффициенты из этой группы по формулам (2).

Гипотезы об информационной способности и адекватности построенных полиномиальных моделей проверяются методами регрессионного анализа.

Пример использования композиционных симметрических планов Бокса В₄ и РКП при оптимизации микроклимата.

Приведем результаты исследований по выбранным факторным планам тепло-влажностного и воздушного режимов в помещениях, расположенных в двухэтажном кирпичном здании [3].

Эксперимент проводился в переходный период отопительного сезона (март-апрель). В здании работала двухтрубная тупиковая система отопления с нижней разводкой, для прогрева высоких помещений были установлены напольные конвекторы, в специальном помещении первого этажа функционировал элеваторный узел.

Значительный налет ржавчины и солей на внутренних стенках отопительных приборов и трубопроводов, возникший из-за сложной конфигурации системы, отсутствия гибкой регулировки между отдельными узлами, невыполнения в течение длительного периода эксплуатации должной очистки и профилактики; отсутствие пылеуловителей, кондиционеров и других воздухоочистительных приборов необходимой мощности, позволяющих отводить избытки тепла, влаги, углекислого газа и других нежелательных веществ, а также многие другие вредные факторы вызвали неблагоприятные изменения метеорологических условий воздуха в обслуживаемой зоне помещений (табл. 1).

Таблица 1. Максимальные абсолютные величины отклоненийэкспериментальных значений от оптимальных норм

Инструментальные обследования метеорологических условий воздуха в помещениях здания показали существенные отклонения экспериментальных значений параметров микроклимата от оптимальных норм, рекомендуемых СНИП.

Для разработки мероприятий по нормализации микроклимата в каждом из помещений при одинаковых (по возможности) условиях были проведены полные факторные эксперименты по планам Бокса B₄ и РКП.

Процесс организации вычислительных процедур продемонстрируем на примере моделирования температурного поля в помещении размерами 3,00 x 9,04 x 8,12 м, расположенном на 2-м этаже здания.

Таблица 2. Кодирование факторов в РКП

Для того чтобы воспользоваться стандартными матрицами планиро­вания X натурные значения фак­торов времени х₁ и пространствен­ных координат х₂, х₃, х₄ переводятся в безразмерные. В табл. 2 показаны 5 уровней варьирования независимых переменных в рототабельном композиционном плане. По плану Бокса В₄ управляемые факторы ко­дируются на трех уровнях с интервалами варьирования Dх₁ = 4, Dх₂ = 1. Dх₃ = 4.02 и Dх₄ = 3,56.

Опытные данные, полученные при исследовании температурного поля в выбранном помещении, приведены в табл. 3. Регрессионные коэффициенты уравнения темпера­тур (1) рассчитываются по формулам (2), табл. 3. Проверка информационной способности и адекватности полученных полиномиальных моделей показала: по РКП F_инф = 2,39, F_ад =1,19, F_таб = 3,91; по плану Бокса F_инф = 1,93, F_ад = 2,10.

Так как вычисленные критерии Фишера меньше табличных, можно предположить. что обе модели адекватны реальному процессу изменения температуры в помещении.

Анализ результатов.

В результате анализа рассчитанных полей температур, влажности и подвижности воздуха был сделан вывод, что наблюдается перегрев помещений и здания в целом, который приводит к всплытию воздушных потоков в верхнюю часть помещений и возникновению теп­ловых подушек с одновременным понижением и без того низкой влажно­сти, с недостаточностью воздухообмена и образованием застойных зон. На основе полученных данных был разработан комплекс мероприятий, который позволил привести метеорологические условия и чистоту воз­духа в обслуживаемой зоне помещений в соответствие с нормами.

Применение статистических методов дает возможность в оптимальные сроки с минимальным количеством опытов определить и исследовать математические зависимости основных параметров тепло-влажностного и воздушного режимов от времени суток и размеров помещения при сформировавшихся в установившемся эксплуатационном режиме здания метеорологических условиях. Планирование экспериментов по исследованию микроклимата в помеще­ниях одновременно по двум симметричным композиционным факторным планам 2-го порядка показало, что количество опытов, требуемых для получения одинаковой максимальной погрешности результатов эксперимента при расчетах на моделях РКП в 2-3 раза меньше, чем при ис­пользовании планов типа В₄ . Однако в случаях, когда хотя бы одна из стен по­мещения является наружной, РКП может приводить к неадекватным математи­ческим моделям. Такой эффект можно объяснить асимметричностью располо­жения в помещении оконных и дверных проемов, через которые происходит неорганизованное поступление наружных воздушных масс, тогда как униформность РКП предполагает практически постоянную дисперсию рассеяния прогно­зируемых значений функции отклика вокруг центра эксперимента.

Таблица 3. Коэффициенты уравнения регрессии для температуры

СПИСОК ЛИТЕРАТУРЫ

1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий - М.: Наука, 1976.
2. Сергиенко Л.С., Житов В.Г. Исследование метеорологических условий в помещениях жилых и общественных зданий с применением математических методов планирования эксперимента //Известия высших учебных заведений Министерства образования РФ / Ежемес. науч.-теорет. журн. "Строительство" - № 6 (534). - Новосибирск: Изд-во Новосиб. гос. архитектурно-строительного ун-та, 2003. - С. 63-67.
3. Сергиенко Л.С., Житов В.Г. О компьютерном моделировании микроклимата в здании //Матем. модели и методы их исследования / Тр. междунар. конф., Т. 2. - Красноярск: Изд-во ИВМ СО РАН, 2001. - С. 191-195.