Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Закон сохранения импульса тел в общем виде записывается так:

P₁ + P₂ = P,                           (1)

где P₁ и P₂ - первоначальные импульсы тел, P - конечный импульс тел.

Когда первоначальные импульсы тел будут равны, т.е.:

Р₁ = Р₂ = Р,                           (2)

то закон сохранения импульса будет иметь вид:

Р₁ + Р₂ = 2Р                         (3).

Учитывая, что

Р = FΔt = mV,                    (4)

где m - масса материальной точки, V - ее скорость, F - сила, Δt- элементарное время.

И подставляя уравнение (4) в уравнение (3), получим:

F₁ Δt+ F₂ Δt= 2 mV.        (5)

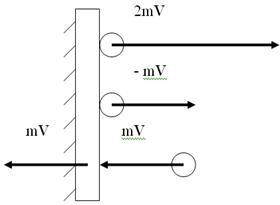
Рассмотрим упругий удар молекулы о стенку.

Пусть V - скорость молекулы, направленная перпендикулярно к стенке, а m - масса. При упругом ударе молекула сообщает стенке импульс mV, после удара ее импульс станет равным - mV. Следовательно, импульс молекулы изменится на:

mV - (-mV) = 2 mV.          (6)

По второму закону Ньютона:

Ft = 2 mV.                            (7)

Согласно закона сохранения импульса: импульс до взаимодействия тел равен импульсу после взаимодействия. Но:

mV ≠ 2 mV                        (8)

(см. рис. 1), т.е. нарушается закон сохранения импульса тел. Кроме того, второй закон Ньютона нельзя применять к уравнению (6) потому, что импульсы и силы F₁ и F₂ приложены к разным телам.

Наш вариант решения

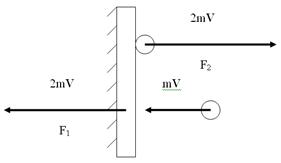
До взаимодействия молекулы со стенкой F₂ = 0, тогда из уравнения (5) следует:

F₁Δt = 2 mV.                      (9)

Когда стенка подействует на молекулу, то F₁Δt = 0. Из уравнения (5) следует:

F₂ Δt= 2 mV.                      (10)

Согласно закона сохранения импульса: импульс до взаимодействия тел равен импульсу после взаимодействия (см. рис. 2).

Учитывая уравнение (4), уравнение (9) будет иметь вид:

mV = 2 mV.                         (10)

Если возвести обе части равенства (10) в квадрат, получим:

V² = 4V²                ,                              (11)

откуда

V =  V,                           (12)

тогда получается, что мы имеем две разные скорости: мгновенную скорость при ударе V_мгн и среднюю скорость V_ср после удара. Уравнение (12) запишется так:

V_мгн =  V_ср                     (13).

Интересно заметить, что при изучении переменного тока существует такое равенство:

I_m = I_эф,

где I_m - амплитудное значение тока, I_эф - эффективное или действующее значение тока. Амплитудный ток - максимальный, эффективный ток - средний

А почему такого уравнения не может быть в механике?

При выводе формулы средней длины свободного пробега молекул физики вводят поправочный коэффициент  без теории. Но таким образом можно ввести любой коэффициент, например, .

Мы думаем, что в уравнении:

= 4 r² n₀,                         (14)

где r - радиус молекулы, n₀ - концентрация молекул, надо вместо средней скорости молекул  поставить мгновенную скорость молекул V_мгн. Тогда уравнение (14) должно записаться так:

= 4 r² V_мгн n₀.                           (15)

Подставляя уравнение (13) в уравнение (15) получим конечное, без поправочного коэффициента уравнение, по которому определяют среднюю длину свободного пробега молекул:

= 4 r² n₀.            (16)

Из всего сказанного делаем резюме:

1. Закон сохранения импульса тел, при ударе, отличается от общепризнанного, прежде всего записью;
2. Формула (5), выведенная из закона сохранения импульса тел, позволяет четко и ясно определять взаимодействие между молекулами и телами при ударе, не нарушая закона сохранения импульса тел;
3. Уравнение (13) позволяет теоретически доказать формулу средней длины свободного пробега молекул, не прибегая к поправочному коэффициенту.

СПИСОК ЛИТЕРАТУРЫ:

1. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. - Москва, «Высшая школа», 2001 г., с.30, с.94, с.104