![]() или
или ![]() (1)
(1)
Это преподносится как аксиома и делается два неоспоримых вывода: 1) если путь ![]() , то сила никакой работы не совершает; 2) если сила и перемещение перпендикулярны друг другу, то работа силы равна нулю (
, то сила никакой работы не совершает; 2) если сила и перемещение перпендикулярны друг другу, то работа силы равна нулю (![]() ).
).
В самом раннем советском курсе физики О.Д.Хвольсона [1] последовательность изложения материала была такова: сила F - импульс силы ![]() - количество движения (импульс тела)
- количество движения (импульс тела)![]() - живая сила (кинетическая энергия)
- живая сила (кинетическая энергия) ![]() - работа A.
- работа A.
В современных курсах физики об импульсе силы упоминается мало. Упор делается на импульс тела, приводится формула для работы (1), а затем вводится понятие кинетической энергии. Вот как это делается, например, в курсе физики [2]. Записывается II закон Ньютона для случая разгона неподвижного свободного тела горизонтальной силой
![]() (2)
(2)
Умножают правую часть на V, а левую на ![]() :
:
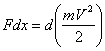 и
и 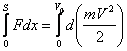 (3)
(3)
После интегрирования получаем:
![]() или
или ![]() (4)
(4)
Если сила F направлена под углом α к горизонту, то в движении участвует только горизонтальная составляющая силы, т.е. ![]() . Отметим, что КПД процесса разгона
. Отметим, что КПД процесса разгона 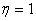 . Смысл формулы (4) таков: сила F, перемещая тело массы m на расстояние S, совершает работу A, результатом которой является изменение кинетической энергии K. Аналогично вычисляется и изменение потенциальной энергии
. Смысл формулы (4) таков: сила F, перемещая тело массы m на расстояние S, совершает работу A, результатом которой является изменение кинетической энергии K. Аналогично вычисляется и изменение потенциальной энергии
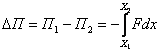 (5)
(5)
Совпадение выражений (3)-(5) приводит к закону сохранения и превращения механической энергии, понятию консервативных сил и потенциальных полей. Приведем более простой вывод формулы (4). Записываем II закон Ньютона: 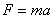 и умножаем обе части уравнения на S:
и умножаем обе части уравнения на S:![]() . Поскольку
. Поскольку ![]() , то получим
, то получим ![]() или
или ![]() . Для работы, совершаемой силой трения, предлагается такая же формула
. Для работы, совершаемой силой трения, предлагается такая же формула ![]() . При движении с трением горизонтальную силу F представляем в виде суммы
. При движении с трением горизонтальную силу F представляем в виде суммы ![]() , где сила
, где сила ![]() вызывает ускоренное движение тела в соответствии со II законом Ньютона.
вызывает ускоренное движение тела в соответствии со II законом Ньютона.
Рассмотрим несколько случаев движения тела массы ![]() кг при действии на нее силы
кг при действии на нее силы ![]() Н в течение времени
Н в течение времени ![]() с. Если есть трение, то коэффициент трения скольжения
с. Если есть трение, то коэффициент трения скольжения ![]() , угол
, угол ![]() . Во всех случаях
. Во всех случаях ![]() м/с (за исключением случая подъема тела вверх, где
м/с (за исключением случая подъема тела вверх, где ![]() м/с).
м/с).
Таблица 1. Расчеты
|
Схема движения |
|
|
|
|
|
|
|
Потеря энергии
|
|
1. |
100 |
10 |
500 |
- |
50 |
- |
|
0 |
|
2. |
86,6 |
8,66 |
433 |
- |
37,5 |
- |
37,5 |
-12,5 |
|
3. |
80 |
8 |
400 |
20 |
32 |
8 |
40 |
-10 |
|
4. |
76,6 |
7,66 |
383 |
10 |
29,34 |
3,83 |
33,17 |
-16,83 |
|
5. |
|
0,2 |
|
- |
0,02 |
|
1 |
-49 |
|
6. |
- |
- |
- |
|
- |
- |
0 |
-50 |
Из этой таблицы следует, что один и тот же импульс силы ![]() Н∙с, воздействуя на одно и то же тело массой m=10 кг, производит разное количество работы: от 0 до 50 кДж. Куда же девается энергия, приведенная в последнем столбце таблицы? Разумно ожидать, что один и тот же импульс силы, воздействуя на одно и то же тело, воспроизведет одно и то же количество энергии (работы). Для чего же тогда существуют так называемые законы сохранения? Следует пересмотреть правомерность формулы (1), для чего проинтегрируем уравнение (2). Для случая постоянной силы:
Н∙с, воздействуя на одно и то же тело массой m=10 кг, производит разное количество работы: от 0 до 50 кДж. Куда же девается энергия, приведенная в последнем столбце таблицы? Разумно ожидать, что один и тот же импульс силы, воздействуя на одно и то же тело, воспроизведет одно и то же количество энергии (работы). Для чего же тогда существуют так называемые законы сохранения? Следует пересмотреть правомерность формулы (1), для чего проинтегрируем уравнение (2). Для случая постоянной силы:
![]() или
или ![]() (6)
(6)
Т.е. свободное тело под действием импульса силы I приобретает численно равное ему количество движения (импульс тела) P. Возводя в квадрат равенство (6) и разделив его на 2m, получим:
![]() или
или ![]() (7)
(7)
Т.е. получили другое выражение для работы, связанное с импульсом силы и массой тела и никак не связанное с путем, проходимым телом. Отметим, что правые части уравнения (2) и (7) могут быть равны нулю, если под действием импульса силы тело не изменяет свою скорость (движется равномерно при наличии трения) или остается неподвижным (![]() ). Таким образом формула (8) более универсальна, чем (1). Формула (1) является частным случаем (7): т.к. при движении из состояния покоя
). Таким образом формула (8) более универсальна, чем (1). Формула (1) является частным случаем (7): т.к. при движении из состояния покоя 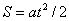 , ускорение
, ускорение ![]() , то
, то 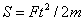 и формула (7) преобразуется к стандартной форме:
и формула (7) преобразуется к стандартной форме:![]() . На основе формулы (7) можно дать другое определение работы: работа - это производство энергии импульсом силы.
. На основе формулы (7) можно дать другое определение работы: работа - это производство энергии импульсом силы.
Для вычисления отдельных видов работ необходимо составить баланс импульсов сил. В общем случае энергия, подводимая к телу в виде импульса силы 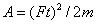 идет на создание кинетической энергии
идет на создание кинетической энергии 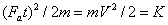 и на совершение работ трения
и на совершение работ трения ![]() , деформации
, деформации ![]() и левитации
и левитации ![]() . Работа левитации
. Работа левитации ![]() совершается силой, направленной вертикально вверх. Если
совершается силой, направленной вертикально вверх. Если ![]() , то тело будет находиться в квазиневесомом состоянии (состоянии левитации). Для схем движения 2 и 4 (табл.1)
, то тело будет находиться в квазиневесомом состоянии (состоянии левитации). Для схем движения 2 и 4 (табл.1) ![]() . Говорят, что если неподвижный человек держит груз, то он не совершает работы, т.к. путь
. Говорят, что если неподвижный человек держит груз, то он не совершает работы, т.к. путь ![]() . А если человек несет груз, то работу тоже не совершает, т.к. сила тяжести груза перпендикулярна пути (
. А если человек несет груз, то работу тоже не совершает, т.к. сила тяжести груза перпендикулярна пути (![]() ). На самом же деле в обоих случаях совершается работа левитации.
). На самом же деле в обоих случаях совершается работа левитации.
Если на тело действует горизонтальная сила F, то баланс импульсов сил можно записать в следующем виде:
![]() (8)
(8)
Здесь учтено, что ![]() . Возводя в квадрат обе части равенства и разделив все на 2m, получим баланс энергий (работ):
. Возводя в квадрат обе части равенства и разделив все на 2m, получим баланс энергий (работ):
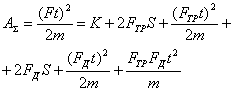 (9)
(9)
Если деформация отсутствует, то
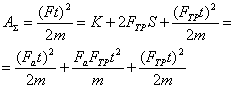 (10)
(10)
Расчет по (10) схемы 3 дает работу 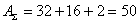 кДж. Если трение отсутствует, то
кДж. Если трение отсутствует, то
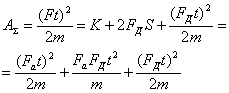 (11)
(11)
Уравнение (9) сильно отличается от выражения (4), которое дает КПД ![]() , что физически нереально. Любое тело при попытке привести его в движение упруго деформируется. Если при действии импульса силы тело остается неподвижным (K и S равны нулю), то
, что физически нереально. Любое тело при попытке привести его в движение упруго деформируется. Если при действии импульса силы тело остается неподвижным (K и S равны нулю), то
![]() (12)
(12)
Этот случай соответствует схеме 6. Если тело испытывает упругую деформацию, то возникают упругие колебания, которые вследствие дисперсии и внутреннего трения затухают, переходя во внутреннюю энергию (тело нагревается). Если импульс силы очень велик, то он вызовет пластическую деформацию. Этот случай эквивалентен абсолютно неупругому удару, когда тело небольшой массы, обладая импульсом ![]() , налетает на массивное неподвижное тело
, налетает на массивное неподвижное тело ![]() . Почти вся кинетическая энергия переходит во внутреннюю энергию [2]:
. Почти вся кинетическая энергия переходит во внутреннюю энергию [2]:
![]()
Для схемы 4 баланс импульсов сил: ![]() , где
, где ![]() ,
, ![]() , а баланс энергий (работ):
, а баланс энергий (работ):
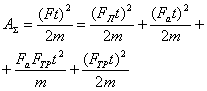 (13)
(13)
Подставляя числовые значения, получим:
![]() кДж.
кДж.
Для схемы 5 баланс импульсов сил: ![]() , где
, где ![]() . Возведя его в квадрат и разделив на 2m, получим баланс энергий (работ):
. Возведя его в квадрат и разделив на 2m, получим баланс энергий (работ):
![]() (14)
(14)
Подставляя числовые значения, получим:
![]() .
.
Из проведенного анализа можно сделать следующие выводы. Работа - это производство энергии импульсом силы ![]() . Один и тот же импульс силы I, воздействуя на одно и то же тело массы m, совершит всегда одну и ту же работу
. Один и тот же импульс силы I, воздействуя на одно и то же тело массы m, совершит всегда одну и ту же работу ![]() .
.
СПИСОК ЛИТЕРАТУРЫ
- Хвольсон О.Д. Курс физики. - Берлин: госуд. изд-во. - 1923. - Том 1.
- Матвеев А.Н. Механика и теория относительности. - М.: Высш. шк., 1986.




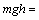 =0,98
=0,98