В земных условиях лишь небольшие капли принимают форму шара. Это связано с тем, что свободная энергия поверхности убывает пропорционально площади, т.е. квадрату линейных размеров, а сила тяжести, действующая на каплю, убывает пропорционально ее массе, т.е. кубу линейных размеров. Поэтому при уменьшении размеров капель их поверхностная энергия превалирует над силой тяжестью и маленькие капли принимают форму близкую к сферической.
Если поверхность жидкости искривлена, то при равновесии давление по разные стороны ее должны быть разными.
В общем случае кривизна поверхности определяется главными радиусами кривизны R1 и R2 .
Разность давлений дается выражением
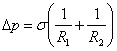, (1)
которое называется формулой Лапласа.
Здесь σ -поверхностное натяжение жидкости.
Испарение жидкости, как правило, происходит с поверхности. Поэтому изменение свойств поверхностного слоя должно изменить условия равновесия между жидкостью и паром над ней. В частности, на условиях равновесия, а значит, и на упругость насыщенного пара должна сказаться кривизна поверхности жидкости.
При рассмотрении испарения капель, лежащих на плоских поверхностях твердых тел, при равновесии системы жидкость-твердое тело-пар, в качестве основной характеристики используется краевой угол θ.
В том случае, когда трехфазная система не находится в равновесии, соответствующий угол называется контактным углом, обозначаемым также θ. В обоих случаях величина θ определяется удельными межфазными избыточными энергиями соприкасающихся фаз.
Нетрудно вычислить, насколько упругость насыщенного пара над кривой и плоской поверхностями отличаются друг от друга.
Представим себе закрытый сосуд с жидкостью, в которую частично погружена капиллярная трубка. Проведем рассуждения в предположении, что жидкость смачивает стенки капилляра (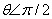
). Случай несмачивания ( 
) может быть рассмотрен точно так же.
Тогда, соотношение между давлением насыщенного пара над искривленной и плоской поверхностями запишется в виде
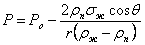, (2)
где r - радиус капилляра, ρж и ρп - плотности жидкости и пара. Обычно ρж >> ρп , поэтому плотностью пара в знаменателе (2) можно пренебречь.
Из формулы (2) без каких -либо дополнительных условий следует, что значение косинуса краевого угла определяет знак дополнительного давления на искривленной поверхности. В случае θ < π/2 , косинус краевого угла больше нуля cos θ > 0 и давление насыщенного пара над вогнутой поверхностью жидкости меньше, чем над плоской поверхностью жидкости в широком сосуде. При θ > π/2, cos θ < 0 и давление насыщенного пара над выпуклой поверхностью жидкости больше, чем над плоской. Отсюда следует, что θ оказывает существенное влияние на дополнительное давление, возникающее на искривленных поверхностях раздела, а следовательно, на процесс испарения жидкостей, в частности, при испарении дождевых капель, лежащих на листьях растений.
Формула (2) справедлива не только в случае, когда поверхность искривлена из-за того, что она находится в капилляре, но и в тех случаях, когда капля жидкости находится в паре (выпуклая поверхность) или она лежит на поверхности твердого тела. Она справедлива также, для газового пузырька, находящегося в жидкости (вогнутая поверхность).
В естественных условиях могут реализовываться всевозможные виды контакта жидкости с твердой поверхностью.
Как показывают наблюдения после дождя с некоторых сортов трав и культурных растений вода быстро испаряется ( θ < π/2 ), в то время как на других достаточно долгое время остаются капли воды (дождя). Наличие растений, не смачивающихся водой (θ > π/2) частично может предохранять травостой от преждевременного высыхания. К растениям, которые не смачиваются водой, например, относятся клевер и листья капусты.
В качестве примера найдем время испарения водяной капли с начальным радиусом 
в воздухе с относительной влажностью ƒ при температуре Т. Обозначим плотность насыщенного водяного пара над плоской поверхностью при данной температуре f
, коэффициент диффузии пара -D.
Масса пара, ежесекундно диффундирующая через сферическую поверхность радиуса r, концентрическую с поверхностью капли, равна
(3)
где ρ -плотность пара, D -коэффициент диффузии.
Если процесс стационарный, то m не будет зависеть от радиуса r . Из (3), получим
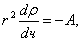(4)
где 
. Интегрирование (4) , дает
(5)
где ρ ∞ -плотность пара на бесконечном расстоянии от капли. Величина А найдется из условия, что при r = a (a -радиус капли, меняющийся во времени) пар должен быть насыщенным. Тогда,
, (6)
(7)
Теперь рассмотрим испарение капли воды той же массы, но лежащей на поверхности твердого тела.
Масса капли, лежащей на твердой поверхности равна:
. (8)
Так как массы, определяемые формулами (7) и (8) одинаковы, то
(9)
Интегрируя (9) и пренебрегая зависимостью ρнас от кривизны поверхности капли, получим
. (10)
Капля воды испарится за время
. (11)
С учетом влажности воздуха формула (11) перепишется в виде
, (12)
где f - относительная влажность воздуха в том месте, где происходит испарение капель дождя.
Отметим, что в частном случае формула (12) (θ =1800 ) переходит в формулу, приведенную в [1]. Преимущество (12) состоит в том, что 
может быть любым. В формуле, приведенной в [1] происходит испарение капель, находящихся в тумане во взвешенном состоянии. Если масса капли велика, то она естественно упадет на поверхность какого-либо тела, т.е. (12) более практична. Например, для капли воды с первоначальным радиусом = 5 мм, лежащей на листьях растений с контактным углом θ = 1200 в воздухе с относительной влажностью f=40% при Т= 293 К, время испарения составляет около 13 часов. Плотность насыщенного пара над плоской поверхностью при этой температуре принята равной ρнас = 1,7 10-2 кг/м3 , а коэффициент диффузии пара
D = 0,22 · 10-4м2/с.
Из (12) следует, что при θ = 00, t = 0.
В заключение отметим, что формула (12) позволяет регулировать время испарения капли дождя, что открывает большие возможности использования данного метода для предотвращения преждевременного высыхания трав и различных культурных растений в засушливых местах.
СПИСОК ЛИТЕРАТУРЫ
- Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М.: Наука, 1979.-551с.