Неравномерность движения порождает ряд проблем динамического характера: переменный приведенный момент внешних сил возбуждает в приводе вынужденные колебания опасные в узких областях, близких к собственным частотам, а переменный приведенный момент инерции механизма - параметрические колебания, опасные в нескольких полосах частот, соответствующих главным, побочным и комбинационным резонансам, и имеющих тенденцию к расширению. Поэтому моделирование динамики приводов таких машин является актуальной задачей с точки зрения обеспечения их надежности. Учитывая разнообразие структурных и кинематических схем механизмов, сформулируем общие методологические принципы такого моделирования.
В начале в функции обобщенной координаты механизма φk, - угла поворота главного вала, определяют траектории движения центров масс в проекциях на координатные оси xi(φk,), zi(φk)и углы поворота звеньев φi(φr). Затем дифференцированием по обобщенной координате находят аналоги линейных и угловых скоростей: x/i(φk); z/i(φk); φ/i(φr) и ускорений: x//i(φk); z//i(φk); φ//i(φk). На основании полученных аналогов определяют приведенные моменты внешних сил Mk и инерции механизма θk:
![]()
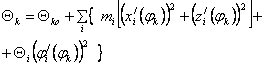 ,
,
где Fxi,Fzi - проекции на координатные оси внешних сил, приведенных к центру масс i-го звена; Мi - момент внешних сил, действующих на i-е звено; θko-собственный момент инерции главного вала; mi, θi -масса и момент инерции i - го звена.
Затем на основании уравнений Лагранжа второго рода составляются уравнения движения каждого дискретизированного элемента привода, причем для главного вала машины оно будет иметь вид:
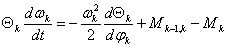 ,
,
а для прочих j-тых
![]()
где ωj=dφj /dt - угловая скорость j-того элемента привода; Mj+1, Mj-1 - моменты в упруго- диссипативных и упруго-пластичных связях между элементами привода.
![]()
Где
![]()
![]()



