(1)
Эта функция может быть использована при оценке уровня микроускорений на борту орбитального космического аппарата ( КА ) [1].
При полном отсутствии или слабом демпфировании собственных колебаний упругих элементов микроускорения можно рассматривать как случайную величину, а изменением числовых характеристик пренебречь [2]. В реальности для оценки уровня микроускорений, прежде всего, квазистатической его компоненты, исследователи ограничиваются рассмотрением первых нескольких форм колебаний упругих элементов КА, а это как раз рассматриваемый случай.
Прежде всего, необходимо выяснить в каком диапазоне параметров ФВМ также подходит под понятие случайной величины. При малых значениях фрактальной размерности D ФВМ значительно возрастает и, следовательно, может рассматриваться как случайный процесс. При D выше 1,99 роста функции не наблюдается. Исследования показывают, что в диапазоне фрактальной размерности 1,95<D<2 ФВМ можно считать с достаточной точностью случайной величиной.
Диапазон изменений b выбирается, исходя из постановки задачи, которая более подробно изложена в работах [3, 4]. Здесь следует отметить лишь интересную особенность: при 0<b<1 и достаточно больших значениях D ( выше 1,99 ) наблюдается следующий эффект. При увеличении фрактальной размерности все значения функции синхронно возрастают, а вид самой ФВМ остается прежним, т.е. ФВМ оказывается «поднятой» вверх. Такой эффект очень полезен при моделировании микроускорений в указанной постановке задачи и означает, что увеличен момент управляющих ракетных двигателей ( УРД ), который связан с угловым ускорением и соответственно микроускорениями известными соотношениями:
,
где I - момент инерции КА, а R - расстояние от рассматриваемой точки до центра масс КА.
Вообще говоря микроускорения определяются еще и своей нормальной составляющей, но в силу того, что угловая скорость вращения КА входит туда во второй степени, нормальным ускорением можно пренебречь как существенно более малой величиной по сравнению с касательным ускорением.
Таким образом, для моделирования микроускорений подходит коридор изменения параметров ФВМ: 0<b<1, 1,99<D<2 [4].
После выявления этого диапазона следует статистически построить закон распределения ФВМ. Исследование законов распределения начнем с самого простого предположения о гауссовом распределении, а для проверки этой гипотезы воспользуемся критерием согласия хи-квадрат Пирсона. При проверке значения ФВМ выбирались из интервала значений t от 0 до 1 с шагом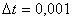 
. Т.е. анализировалась выборка, состоящая из 1000 точек, которая последовательно разбивалась на 4, 6, ... , 30 диапазонов. Причем, левая граница (4 диапазона) обусловлена предельно допустимой погрешностью построения теоретической функции плотности вероятности, а правая (30 диапазонов) - количеством точек в выборке. Точка ( 0; 0 ) не входила в анализ, ее выбраковываем как выброс. На каждом из значений параметров рабочего диапазона проверялась гипотеза о гауссовом распределении. Исследования показали, что во всех случаях, за единичными исключениями крайних (4 или 30) диапазонов критерий согласия не позволяет сделать вывод о том, что ФВМ подчиняется гауссовому закону распределения. Поэтому следует выдвигать и проверять гипотезы о более сложном, чем нормальный законе распределения ФВМ [5].
СПИСОК ЛИТЕРАТУРЫ
- Седельников А.В., Бязина А.В., Иванова С.А. Статистические исследования микроускорений при наличии слабого демпфирования колебаний упругих элементов КА //Сборник научных трудов в Самарском филиале УРАО. ч. 1. Самара. 2003. с. 137 - 158.
- Седельников А.В. Статистические исследования микроускорений как случайной величины //Фундаментальные исследования. №6. 2004. с. 123-124.
- Седельников А.В., Бязина А.В. Использование фракталов в математическом моделировании //Сборник научных трудов в Самарском филиале УРАО. вып. 2-3. Самара. 2002. с. 72 - 85.
- Седельников А.В. Исследование функции распределения уровня микроускорений во времени //Успехи современного естествознания. - 2004. - № 9. - с. 15-18.
- Седельников А.В., Бязина А.В. Исследование законов распределения микроускорений, смоделированных с помощью функции Вейерштрасса-Мандельброта и полученных в результате эксперимента //Современные проблемы механики и прикладной математики. - Сборник трудов международной школы-семинара. - Ч. 1. - т. 2. - Воронеж. - 2004. - с. 450-453.