Проблема расчета подрессоренной массы сама по себе является весьма сложной задачей. Недостаточно изучена проблема, когда подрессоренная масса содержит (или содержится) как один из своих элементов, так же подрессоренную массу. Такая ситуация возникает в случаях проектирования автовозов. При проецировании задачи моделирования и расчета подрессоренной массы итерационно компонентных объектов на предметную область автовозов, происходить некоторое сворачивание проблемы, так как в рамках решения будет использоваться упрощенная модель. Упрощенность модели следует из того, что «верхний слой» (непосредственно автомобиль, транспортируемый автовозом) будет опосредованно воспринимать неоднородность дороги. Это вызвано статичностью его горизонтального состояния относительно платформы автовоза (существуют горизонтальные моменты, возникающие при ускоренном, замедленном и центробежном ускорении, но при условии жесткой фиксации опоры действиями этих сил на перемещение опоры перевозимой машины можно пренебречь), что и позволяет обоснованно использовать упрощенную модель.
В то же время задачу поведения автомобиля на некоторой поверхности можно определить как класс задач в построениях 3d сцен. Использование сложных физических решателей чаще всего не обосновано, так как ведет к чрезмерному усложнению задачи. Таким образом, получаем гибридную область на стыке предметных областей: физический расчет подвески и реалистичное моделирование физики подвески в 3d сценах.
Моделирование поведения подвески осуществляется на входном наборе неоднородности дороги, а так же с учетом параметров подвески. Дорога рассматривается как равномерно неоднородная поверхность с внесенной, статически повторяющейся компонентой (выбор такой модели обусловлен необходимостью контроля выходного результата на соответствие).
В данной работе рассматривается метод генерации случайного равномерного рельефа и поведения автомобиля на этом рельефе. Для генерации рельефа была использована трехмерная регулярно повторяющаяся структура с внесенной в нее неоднородной составляющей. Для придания однородности ландшафтному полю в качестве базовых составляющих были использованы периодические тригонометрические функции (sin(), cos()). Для адекватного отражения моделью реальных условий была введена неоднородность поверхности. Методом искажения исходной поверхности является суммирование со случайной равномерно распределенной величиной, не превышающей половину максимальной амплитуды используемых тригонометрических функций. В результате такая поверхность обладает всеми свойствами ландшафта, так как имеет глобальную неоднородность из-за использования случайной функции, а так же периодических функций, которые являются континуальными (вводимая случайная величина вносит дискретность только на момент генерации новой сетки). Для сглаживания используются интегральные функции, которые позволяют рассчитать контакт не только в точке соприкосновения, а по всему пятну контакта. В модель введена вероятность «непреодолимого препятствия», что позволяет учитывать такие «географические» участки «ландшафта» на которых движение невозможно, так как перепады уровня составляют более 0.3 диаметра колеса.
Практической реализацией расчета динамики подвески автомобиля при воздействии ландшафта стала разработка автоматизированной системы, реализующей модель взаимодействия автомобиля с внешней средой (ландшафтом). Для расчета поведения применяется сглаживающий фильтр на наборе входных параметров, при этом учитывается состояние дороги не только в точке контакта, но используется целиком пятно контакта, что позволяет избежать коллизий при отображении взаимодействия. Так же в расчете применяется модель критической неоднородности для тех случаев, когда величина неоднородности больше одной четверной радиуса колеса, при такой ситуации колесо просто не может пройти через препятствие, что соответственно ведет к деформации конструкции.
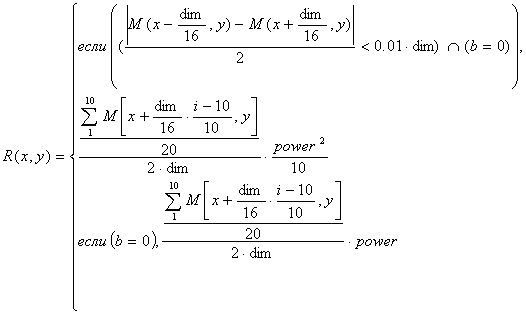
где R(x,y) - сила, действующая на подвеску в точке с координатами (x,y);
M(x,y) - высота рельефа в координате пространства (x,y);
dim - диаметр колеса моделируемого автомобиля;
power - жесткость подвески.
Полученные результаты с весьма большой степенью соответствуют поведению подвески автотранспорта на неоднородном ландшафте, что позволяет говорить об успешном решении поставленной задачи.
Результаты исследований:
- в результате проведенной адаптации существующей модели расчета динамики подвески была получена новая модель, упрощающая расчет динамики подвески;
- полученная модель расчета была проверена на адекватность в MathCAD и показала достаточный уровень достоверности;
- была подготовлена и импортирована 3d модель автомобиля для демонстрации работоспособности разработанной модели расчета динамики подвески;
- разработана автоматизированная система, позволяющая проводить моделирование поведения динамики подвески автомобиля при взаимодействии с неоднородным ландшафтом.



