![]() (1)
(1)
Интервал времени измерения ![]() - дискретное линейно упорядоченное множество. Строка y магнитограммы U - канал cy(t) - функция, определенная на этом множестве, с областью значений [0,1023]. Тогда исходные данные - магнитограмма
- дискретное линейно упорядоченное множество. Строка y магнитограммы U - канал cy(t) - функция, определенная на этом множестве, с областью значений [0,1023]. Тогда исходные данные - магнитограмма
![]() (2)
(2)
- это множество функций, определенных на T.
Канал является целочисленной функцией времени и представляет собой упорядоченную по времени последовательность значений, полученных с одного и того же датчика y, и является моделью динамики изменения магнитного потока над этим датчиком в течение времени измерения. Магнитограмма является логическим объединением множества этих процессов потому, что это процессы независимые, ненормированные и стохастические. Поскольку аппаратные функции датчиков неизвестны, классический метод решения обратной задачи сведением к интегральному уравнению Фредгольма 1 рода типа свертки неприменим [1]. Поэтому приходится рассматривать канал как набор испытаний случайной величины с постоянной вероятностью.
Шов ориентирован строго вертикально, совпадает с колонкой магнитограммы. Субъективно он воспринимается за счет кратковременного синхронного увеличения амплитуды колебаний уровней сигнала, причем не обязательно во всех каналах. В качестве наиболее информативного в контексте обнаружения швов компонента сигнала примем вариативность сигнала на отрезке, равном средней «толщине» шва - средней «продолжительности» этого увеличения.
Результат распознавания представим в виде результирующей функции v(t) с областью определения T и множеством значений [0,1], где 0 будет моделью события «шов не найден», а 1 - моделью события «шов найден».
![]() (3),
(3),
Разработан целый ряд методов распознавания, которые можно поделить на классы следующим образом [3]:
- методы непосредственного сравнения с эталоном;
- методы, основанные на ортогональных преобразованиях исходного изображения;
- синтаксические методы;
- методы, основанные на вычислении признаков исходного изображения с последующей классификацией методами кластерного анализа.
Существуют и другие классификации подходов к решению задач распознавания, например, показанная в [4]:
- эвристический;
- формальный математический;
- структурный;
или, на другом уровне абстракции:
- статистический;
- детерминистский;
- логический;
- синтаксический;
- нейросетевой;
- корреляционный;
и множество других классификаций. Рассмотрим вкратце возможность применения этих методов для решения данной задачи.
«Шов» - это целый класс явлений, обладающих общностью лишь на достаточно высоком уровне абстракции. Значит понятия «эталон шва» не существует, а, следовательно, методы распознавания, основанные на сравнении с эталоном или методы, основанные на ортогональных преобразованиях исходного изображения, неприменимы. В частности, для решения задач детектирования был развит классический аппарат корреляционных методов обнаружения [2]. Однако на практике попытки построения корреляционных алгоритмов, обеспечивающих инвариантность к искажениям различной природы, сталкиваются с неразрешимыми проблемами. Кроме того, эти методы не могут использоваться в тех случаях, когда объект описывается не эталонным изображением, а вектором признаков или некоторой обобщенной моделью.
Общая теория построения инвариантных алгоритмов детектирования сложных объектов на изображениях до сих пор не разработана, и для каждого нового класса объектов приходится заново конструировать специальные методы и алгоритмы обнаружения.
В [5] показано, что для решения задач распознавания наиболее приемлемым оказывается статистический подход, основанный на множестве достоверных фактов принадлежности объектов к соответствующим классам. Однако в нашем случае конкретных количественных характеристик, позволяющих однозначно классифицировать класс объектов «шов», не существует по причине разнообразия исходных сигналов. Отсюда неприменимы и методы, основанные на вычислении признаков исходного изображения с последующей кластеризацией. При синтаксическом подходе основные сложности решения задачи связаны с отсутствием формальной модели описания структуры распознаваемого сигнала. [4]. В классической постановке задачи распознавания образов существует решающее правило, классифицирующее объекты по значениям их признаков. Это правило основано на предположении, что разным классам соответствуют непересекающиеся области в признаковом пространстве, что позволяет однозначно определить классовую принадлежность объекта [6]. Классическая постановка задачи здесь неприменима, так как у швов не существует количественных признаков, которые бы могли лечь в основу их классификации. Изменения в структуре сигнала в области шва носят настолько случайный и непредсказуемый характер, что их экспертное обнаружение происходит по совокупности косвенных признаков. Ощутимые практические достижения в разработках систем распознавания изображений сегодня достигаются лишь с учетом специфических особенностей конкретной прикладной задачи, а не рекомендациями общей теории, то есть в рамках узкоспециализированных систем. При указанном в [7] разрыве между теорией и практикой распознавания, когда каждая отдельная прикладная задача решается как бы заново, остается актуальным учет специфических особенностей каждой отдельной задачи.
Не выявлено статистических[8] и частотно-временных[9,10] свойств сигнала, на основе которых можно было бы построить достоверный признак для классификации.
Будем считать числовой мерой вероятности обнаружения шва в точке t0 сигнала cy(t) его вариативность на интервале ![]() , где d - средняя длина шва. В качестве меры вариативности примем среднее квадратическое отклонение дискретной случайной величины, чье распределение значений составлено из всех значений cy(t) из этого интервала. Тогда для канала y частная оценочная функция (ЧОФ):
, где d - средняя длина шва. В качестве меры вариативности примем среднее квадратическое отклонение дискретной случайной величины, чье распределение значений составлено из всех значений cy(t) из этого интервала. Тогда для канала y частная оценочная функция (ЧОФ):
Мы получили множество вещественных функций
![]() (5)
(5)
которые являются независимыми ненормированными оценками вероятности обнаружения шва в каждый момент времени t. Поскольку свойства формирующих каналы датчиков различны, то различны и статистики вычисленных мер вариативности. Значит, одна и та же оценка вариативности в разных каналах имеет разный смысл: значительно превышающая другие в рамках одного канала оценка (хороший кандидат в швы) может быть «поглощена» среднестатистической (фоновой) большей по абсолютной величине оценкой в более «дребезжащем» (с большими статистиками оценок) канале при их совместном рассмотрении. Таким образом, общая надежность распознавания уменьшится. Шов «проявляется» в достаточно большом числе каналов, притом довольно слабо. При этом на магнитограмме наличествуют разного рода «шумовые» объекты - порождающие более сильные вариации, но в меньшем числе каналов и, следовательно, могущие иметь сходную суммарную оценку, что также приводит к ухудшению общей надежности распознавания.
Чтобы сократить описание сигнала, нормировать по величине оценки (и тем самым получить возможность прийти к совокупной оценке) и снять влияние высоких случайных «шумовых» оценок, воспользуемся «поканальной бинаризацией» U1, то есть бинаризацией со своим пороговым значением для каждого канала. Для каждого канала y определим пороговое значение by и введем нормированную оценочную функцию (НОФ)
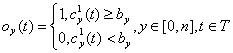 , (6)
, (6)
где «1» будет моделью события «шов обнаружен в канале y в момент времени t», «0» соответствует «шов не обнаружен в канале y в момент времени t». Нормировать частные оценки oy(t) в процессе бинаризации мы можем, получив одинаковое во всех каналах число оценок oy(t), равных 1. Смысл этого в том, что во всех каналах мы получим равное число событий «обнаружен шов» и тем самым выровняем «оценочный вклад» всех каналов независимо от того, насколько сильно отличались в них статистики оценок ![]() . Совокупная оценочная функция (СОФ) будет общей по всем n каналам количественной оценкой вероятности обнаружения шва по сумме нормированных частных оценок:
. Совокупная оценочная функция (СОФ) будет общей по всем n каналам количественной оценкой вероятности обнаружения шва по сумме нормированных частных оценок:
![]() (7)
(7)
В самом простом случае, когда в рассматриваемом фрагменте сигнала всегда имеется один шов, его положение будет определять максимум СОФ на этом фрагменте, а результирующая функция примет вид:
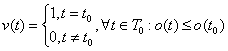 (8)
(8)
Вектор пороговых значений:
![]() (9)
(9)
является оптимальным в смысле надежности распознавания, когда выполняется
![]() (10)
(10)
Надежность распознавания является наилучшей при таком b, когда максимум СОФ отличается от среднего СОФ на наибольшую величину. На практике построение этой зависимости связано с ощутимыми вычислительными затратами, поэтому, если критично время вычисления, удобен другой способ грубой локализации максимума этой зависимости. Максимум зависимости достигается тогда, когда максимум оценочной функции o(t) находится в определенном интервале значений [n1,n2], привязанном к числу каналов n. В практике распознавания швов это интервал [n/5,n/4]. Смысл этого интервала в том, что он обозначает эмпирическое минимально возможное число каналов, «отреагировавших» на шов увеличением вариативности сигнала.
Как правило, в рассматриваемый интервал попадает более одного шва. В этом случае позициям швов соответствуют координаты самых больших локальных максимумов o(t) (назовем их подозрительными точками). При этом, чем круче график o(t) в окрестности подозрительной точки, тем более вероятно, что она порождена швом, а не протяженным шумовым объектом. Имеет смысл анализировать величину локального максимума относительно величины абсолютного (в пределах рассматриваемого фрагмента) максимума. Их отношение редко бывает меньше 1/3. А в качестве меры «крутизны» графика o(t) удобно брать оценку вариативности значений o(t) из некоторой окрестности подозрительной точки, или сумму абсолютных значений производных o(t) в этой же окрестности. При выборе точек локальных максимумов следует учитывать априорное знание о минимальной длине трубы, обуславливающей минимально возможный интервал между координатами подозрительных точек.
Описанный метод реализован в системе экспертного анализа результатов инспекции магистральных газопроводов и успешно применяется в распознавании кольцевых сварных швов. Параметр d (средняя толщина шва) был рассчитан опытным путем, его значение равняется 7. Сигнал обрабатывается пофрагментно, причем длина фрагмента выбирается так, чтобы она превышала максимально возможную длину трубы. Тем самым мы гарантируем наличие хотя бы одного шва в рассматриваемом фрагменте. Значения порогового вектора b вычисляются отдельно для каждого фрагмента. Они выбираются так, чтобы максимум оценочной функции o(t) достигал n/4, а конкретные значения b при этом определяются «шумностью» сигнала в рассматриваемом фрагменте. На сегодняшний день с помощью этого метода обработано 24,73 Тб информации. Было обработано 3010607 кольцевых швов. При этом было пропущено 98361 шов, что составляет 3,2%. Было обнаружено 45468 ложных швов или 1,5% от общего числа обработанных швов. Предпринимались попытки использовать в распознавании швов статистический подход и метод на основе вейвлет-фильтрации, однако они показали гораздо худшую достоверность и гибкость.
СПИСОК ЛИТЕРАТУРЫ
- В. С. Сизиков. Математические методы обработки результатов измерений, С-Пб, 2001
- Ю. В. Визильтер. Методы обнаружения и идентификации объектов сложной формы на изображениях в задачах информационного обеспечения перспективных систем управления : Дис. канд. техн. наук : 05.13.14 Гос. НИИ авиационных систем. М., 1997
- Муратов С. В. Разработка алгоритмов и структур синтаксического распознавания геометрически искаженных изображений : Дис. на соиск. учен. степ. канд. техн. наук : 05.13.13 Ленингр. ин-т точной механики и оптики. Л., 1990
- В. В. Геппенер. Математическое обеспечение многоуровневых систем распознавания сигнальной информации в условиях априорной неопределенности : Дис. ... д-ра техн. наук : 05.13.11 Санкт-Петербург. гос. электротехн. ун-т "ЛЭТИ". СПб., 2000
- А. Х. Нишанов. Разработка и исследование методов определения информационных наборов признаков при распознавании одного типа явлений : Дис. на соиск. учен. степ. канд. техн. наук : 05.13.01 АН УзССР. Узбек. науч.-производ. об-ние "Кибернетика". Ташкент, 1990
- В. В. Моттль. Марковские модели и методы распознавания образов в сигналах с изменяющимися вероятностными свойствами : Дис. на соиск. учен. степ. д-ра техн. наук : 05.13.16 Ин-т проблем управления М., 1993
- М. И. Шлезингер. Теория двумерных грамматик применительно к распознаванию изображений : Дис. на соиск. учен. степ. д-ра физ.-мат. наук : 05.13.16 Ин-т кибернетики им. В. М. Глушкова, Киев, 1990
- Гайдышев И. Анализ и обработка данных, С-Пб, 2001
- Воробьев В. И., Грибунин В. Г. Теория и практика вейвлет-преобразования, С-Пб, 1999
- Sweldens W. The Construction and Application of Wavelets in Numerical Analysis, 1995, PhD Thesis




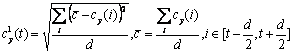 (4)
(4)