Среди систем сухопутной подвижной радиосвязи (ССПР) выделяется особый класс специализированных, или ведомственных систем. Отличительно чертой такого класса является то, что территориальное деление на области/зоны предопределяет ряд внешних, несвязанных с задачей обмена информацией, условий. Например, административное деление территории на округа, районы; разделение зоны действий на участки ответственности между единицами, подразделениями; юридически оформленное разграничение зон застройки и т.п. В таких условиях становиться невозможным применение традиционной техники организации сплошного покрытия с регулярной структурой, широко применяющейся в сотовых сетях. Нерегулярное территориальное деление и неравномерное распределение нагрузки, присущие специализированным сетям, приводят к тому, что методика распределения ресурса канала, становится непригодной. Действительно, указанная методика ориентируется на формирование регулярно повторяющейся частотно-кластерной структуры покрытия территории с помощью операции последовательного спектрального смещения выделенной интермодуляционно совместимой группы частот. В результате сам метод подразумевает регулярную структуру опорной сети и относительно равномерное распределение нагрузки между базовыми станциями.
Второй характерной особенностью специализированных систем является то, что частотный ресурс, выделяемый на каждую область/зону, является фиксированным. Наиболее часто это сводится к тому, что число рабочих частот в области/зоне задается равным некоторому фиксированному значению , достаточному для решения целевой задачи. Кроме того, как правило, существуют нормы частотно-территориального разноса, которые должны обеспечиваться.
Составление частотно-территориального плана при заданных нормах частотно территориального разноса (ЧТР), в общем случае, требует определения групп интермодуляционно совместимых частот присваиваемых базовым радиостанциям системы, покрывающим области, на которые разбита обслуживаемая территория.
Будем полагать, что нормы ЧТР требуют обеспечения интермодуляционной совместимости для частот базовых станций, обслуживающих отдельные области/зоны, на глубину m (областей). Задача частотно-территориального планирования включает в себя два противоречивых условия. С одной стороны требуется на графе зонального деления выделить кластеры минимальной мощности (размеров), каждый из которых имеет радиус не меньше m , а с другой - распределить на них частоты интермодуляционно совместимых групп. Задача выделения кластеров минимальной мощности является классической задачей экспоненциальной сложности, поэтому попытка раздельного решения приводит к неоправданному усложнению. При этом приближенное выделение кластеров приводит к «разрыхлению» пространственной структуры, и, как следствие, к неоправданно высокому использованию частотного ресурса.
Разрешение указанной проблемы вновь предлагается искать на основе развития общего математического аппарата монотонных множеств (систем). Для этого нужно специальным образом сформировать метрику на графе деления рабочей территории на области/зоны.
Примем в качестве меры разноса областей число зон, которые находятся между ними. То есть, если рассмотреть граф, в котором вершины сопоставляются различным областям деления рабочей территории системы, и ребра соединяют вершины, соответствующие граничащим областям, то предлагаемая мера будет однозначно определяться расстоянием на таком графе. При этом ясно, что каждому ребру маршрута присваивается единичный вес, а каждому узлу - нулевой.
Предлагаемый подход позволяет сформулировать задачу следующим образом: на заданной территории, разбитой на некоторые области, необходимо распределить заданное число частот таким образом, чтобы области, отстоящие друг от друга не более чем на m областей, содержали интермодуляционно совместимые частоты.
Решение будем искать без учета возможных эффектов от высоты подъема базовых станций, обслуживающих различные области/зоны, от особенностей рельефа или застройки. Иными словами, ограничимся рассмотрением плоской карты территории, приводящей к однородной метрике маршрутов на эквивалентном графе.
Задача территориального планирования интермодуляционно совместимых частот может быть эффективно решена на базе техники выделения экстремальных подсистем на множествах с монотонной мерой. Только в каждом конкретном случае необходимо специальным образом сконструировать монотонную меру и добиться согласования на уровне физического смысла между решаемой целевой задачей и свойствами формируемого в итоге определимого подмножества (экстремальной подсистемы). Для рассматриваемой задачи также можно воспользоваться указанным подходом.
Сначала введем обозначения:
{
} - множество интервалов частот, из которого следует выбирать необходимые частоты для распределения их на заданной территории, с заданной дискретностью, или просто заданный набор частот.
W - связное ограниченное множество точек плоскости, определяющее территорию, на которой производится частотно-территориальное планирование, 
,
Ai - связное ограниченное множество точек плоскости, определяющее i-ую область (
), причем
, для 
, 
граница между множествами Ai и Aj, представляющая непрерывную кривую на плоскости, либо пустое множество, если Ai и Aj не граничат.
Введем понятие «групп» множеств, отстоящих от заданного множества Aj на расстояние m=0,1..., которые удобно рассматривать как «слои», составляемые узлами, равноудаленными от Aj на эквивалентном графе. В случае m=0 будем под такой «группой» понимать множество 
, элементы которого имеют границы 
с множеством Aj и не содержат сам Aj . Для m=1 - множество 
, элементы которого имеют с множествами границы 
и не содержат ни Aj, ни элементы из . Для m=2 - это множество 
, элементы которого имеют с элементами из границы 
, и которое не содержат элементов из 
, и т.д. Для m=k это такое множество 
, элементы которого имеют с элементами из 
границы 
и не содержат элементов из 
.
Если в качестве множества Aj взять A1, то для m=0 
= {
}, если в качестве множества Aj взять A2, то для m=0 
= {
} = . Аналогично, 
, 
= 
, 
= 
и т.д. Множество 
для A1 при m=1 будет образовано из элементов
= 
.
Обозначим через 
- число элементов множества {
}, или число множеств , входящих в слой с m=0. Тогда 
граница множества Aj. Аналогично определим величину 
- число элементов множества , отстоящих от Aj на один «пролет» (с длинной маршрута 2 на эквивалентном графе). И т. д. Таким образом, для любого целого m можно ввести величины 
, и на их основе определить на множестве W метрику
, (1)
где q - дополнительный операционный параметр, на основе которого ниже вводятся операции воздействия ž и 
на элементы , позволяющие учитывать влияние множеств, отстоящих друг от друга. Чтобы обеспечить согласование с физическим смыслом решаемой целевой задачи вводимые операции для ž и воздействий должны в большей степени проявляться на элементах, близкорасположенных к зоне прямого воздействия, и в меньшей - на удаленных элементах. Это необходимо для корректной работы предлагаемого ниже алгоритма, реализующего технику монотонных множеств. Предлагается подход, позволяющий качественно учитывать три уровня влияния областей/зон по степени создания взаимных интермодуляционных помех. Именно эти уровни определяются значениями параметра q равными 0, 1 или 2. Чем больше величина q, тем более жесткие условия на глубину обеспечения интермодуляционной совместимости по областям накладывает предлагаемая ниже монотонная мера. Следовательно, максимальное значение q=2 приводит к наименьшему коэффициенту повторного пространственного использования частотного спектра. По мере уменьшения q указанный коэффициент растет, но при этом появляется вероятность возникновения ряда пораженных частотных позиций в рабочих диапазонах отдельных областей/зон.
Вес 
определяет максимально допустимую степень влияния частот, распределенных в область/зону Aj, на рабочие частоты, распределенные в соседние множества.
Веденная таким образом метрика позволяет перейти к рассмотрению W как некоторого монотонного множества, на котором могут быть применены быстродействующие процедуры выделения подмножеств областей с заданными экстремальными свойствами, обуславливаемыми взаимным влиянием на уровне ЭМС. Для этого нужно ввести на W операции «отрицательного» ž и «положительного» воздействий. В качестве операции ž, прямо действующей на область/зону Aj, будем понимать преобразование, в результате которого каждому элементу (области/зоне) Ai присваивается новое значение веса:
а) при i=j (рассматривается область/зона прямого воздействия)
, (2)
где k(s,q) =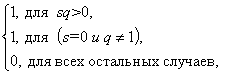 
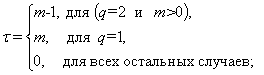
б) при i≠j (рассматривается область/зона вне прямого воздействия)
, (3)
где 
,
= 
Физический смысл введенной операции ž достаточно прост. В начале вес зоны/области Ai равен общему числу других зон (2), для которых она в принципе может создать интермодуляционные помехи. После операции прямого «отрицательного» воздействия на зону Aj вес области Ai в общем случае уменьшается. Действительно, согласно (3), если область Aj находится на расстоянии меньшем, чем задают нормы ЧТР (расстояние на эквивалентном графе меньше m) и q=2, то вес области Ai уменьшается на 1. Это фактически означает об «изъятии» при рассмотрении интермодуляционных помех области Aj.
Аналогично вводится «положительная» операция , прямо воздействующая на элемент (область) Aj. В качестве таковой понимается преобразование, в результате которого каждая область Ai приобретает новое значение веса:
а) при i=j (рассматривается область/зона прямого воздействия)
где 
= 
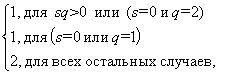
б) при i≠j (рассматривается область/зона вне прямого воздействия)
, (4)
где 
,
= 
Аналогично легко показать, что введенные операции ž, обладают необходимыми свойствами монотонности и коммутативности и, следовательно, однозначно определяют функции множеств 
и 
.
Это позволяет на основе общей процедуры, выделить ž ядро во введенном монотонном множестве W. Выделенное ž ядро содержит элементы (области/зоны), оказывающие наибольшие влияния по интермодуляционному признаку на все остальные элементы (области/зоны) на рассматриваемой территории. Фактически мы получаем в качестве ž ядра некоторое подмножество элементов, которые можно рассматривать как обобщенные центры эквивалентного графа, вычисленные для метрики согласованной с интермодуляционным влиянием зон/областей.
Заранее нужно обратить внимание на то, что приведенный ниже алгоритм предполагает обобщение известной техники выделения ядра (или ядер) монотонного множества, на класс монотонных параметрических мер. В качестве параметров выступают q и m, различные комбинации которых приводят к формированию различных семейств монотонных множеств, к выделению различных определяющих последовательностей, и, как следствие, к формированию параметрического класса ядер, на котором определяется то, которое обеспечивает решение поставленной задачи. При этом экстремальные структуры удается выделить не с помощью полного перебора, а путем алгоритма, имеющего полиномиальную сложность.
Теперь мы можем перейти непосредственно к описанию алгоритма решения поставленной задачи планирования частотно-территориального для специальных ССПР.
Пусть N - максимальное число интермодуляционно совместимых частот, которое можно выбрать из заданного множества частот {φk }. Поскольку способов создания таких множеств может оказаться много, то, в общем случае, будет существовать ни одно такое множество. Будем полагать, что максимальное число множеств из N интермодуляционно совместимых частот 
, таких, что 
, при 
, равно 
. То есть 
.
На множестве зон/областей W выделяем с помощью алгоритма Муллата структуры определяющих подмножеств 
и 
, сходящихся на конечном шаге с номером d к ž ядрам 
и 
, соответственно.
Определяем 
для множеств 
, где 
- это введенные в (2) мощности слоев зон, отстоящих от 
на расстояние s.
Тогда согласно свойствам монотонных множеств (условие монотонности, применительно к введенным весам и операциям), если существует 
, для которого:
1) 
и 
, 
,
2) 
,
3) 
,
4) 
,
то предложенный алгоритм сходится (выделяется последовательность определяющих множеств, сходящихся к соответствующему ядру) к распределению частот, указанному в постановке задачи.