Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Сидоренко Ю.В. Коренькова С.Ф. Стрелкин Е.В.

Статья в формате PDF

157 KB

В настоящее время в строительстве большое внимание уделяется созданию и применению эффективных утеплителей, что связано с повышением требований к теплозащитным свойствам ограждающих конструкций зданий, установленных СНиП II-3-79^**. К числу наиболее перспективных утеплителей относится, в частности, неавтоклавный теплоизоляционный пенобетон, отличающийся эксплуатационной совместимостью с конструкционными материалами, относительно простой технологией производства и распространенностью применяемого (чаще всего - местного) сырья, экологической и  пожарной  безопасностью, долговечностью и т.д.  Его применение особенно востребовано в малоэтажном и сельском строительстве (коттеджи, "теплые" гаражи), для устройства межкомнатных перегородок, наружных стен с использованием керамического кирпича, сайдинга и кругляка (брёвна), чердачных перекрытий и т.п.

Однако часто производимый "легкий" пенобетон (марок D400 и ниже) характеризуется низким уровнем стабильности основных характеристик. Водная составляющая (в цементном тесте и в пене) существенно влияет на формирование структуры пенобетона низкой плотности уже на стадии заливки пенобетонной смеси в форму (индукционный период). Именно для "легких" смесей актуальны вопросы нестабильности, потери устойчивости при укладке их в формы, расслоение фаз. Очевидно, что совершенствованием одного технологического процесса не решить проблему стабильности параметров качества пенобетона. В частности, в научных разработках специалистов все еще остаются открытыми вопросы, затрагивающие теоретическое обоснование  механизма потери устойчивости "легких" пенобетонных смесей с учетом гидродинамических факторов. Трудность решения подобной задачи связана с многофазностью рассматриваемой пенобетонной системы, высокой степенью нестабильности пенной структуры, полидисперсностью твердой и газовой фаз, коллективными явлениями, происходящими  в системе, ее стохастичностью и другими факторами. Таким образом, разработка предложений для решения проблемы нестабильности "легкой" пенобетонной смеси, а, следовательно, и мероприятий по оптимизации неавтоклавной технологии производства теплоизоляционного пенобетона приобретают в настоящее время особую важность и актуальность.

Работы [1-14 и др.] по потере устойчивости пенной структуры показывают, что главная причина этого явления заключается в синерезисе свободной жидкости, происходящем под действием массовых сил. В частности, в [3, 4] рассмотрены частные случаи подобных систем (в основном для вертикального столба пены) и получены математические зависимости по синерезису. Однако реальная пенобетонная структура существенно отличается от классической пенной и, прежде всего - наличием твердой фазы, которая существенно меняет картину и замедляет синерезис по каналам Плато.

Потерю устойчивости легкого пенобетона можно рассматривать как на микроуровне (т.е. отдельной межпоровой перемычке), так и на макроуровне (по отношению к выделенному единичному объему). Решение второй задачи позволило бы, на наш взгляд, определить количественную теоретическую скорость расслоения пенобетонной смеси и выявить влияние на нее различных факторов.

Ценность постановки задачи моделирования устойчивости "легкой" пенобетонной смеси связана с получением модели, которая призвана помочь в прогнозировании поведения пенобетонной системы во время индукционного периода и уточнить  технологические рекомендациями по ее производству. Следует отметить, что к эффективным методам моделирования многофазных систем является применение механики взаимопроникающих континуумов.

Анализ научных работ в этом направлении показывает, что трудность моделирования 3-х фазной системы (пенобетонная смесь) связана с оценкой межфазных взаимодействий по границам фаз. Учитывая это, для формирования математической модели в индукционном периоде (до начала схватывания пенобетонной смеси, находящейся в форме) предлагаем рассматривать 2-х фазную модель, включающую:

твердожидкостную несущую фазу, для которой будут справедливы следующие допущения:

• размеры твердых частиц достаточно малы по сравнению с неоднородностями полей концентраций и скоростей;
• между твердыми частицами отсутствуют процессы агрегации, дробления, а также пренебрегаем взаимодействием между ними;

газотвердожидкостную фазу (так называемый комбинированный кластер), которая равномерно распределена по объему системы и для которой также справедливы вышеизложенные допущения.

Действительно, при формировании структуры легкого пенобетона газовая фаза является каркасом, на котором концентрируется твердая фаза (явление бронирования). Твердая фаза, кроме того, удерживается в области газовой поры связанной водой. Так образуется комбинированный кластер из газовой поры (пузыря), твердых частиц и связанной воды. Подобные кластеры образуют пористую систему, по каналам Плато которой стекает свободная вода в процессе расслоения смеси. Присоединение твердых частиц к кластеру будет определяться балансом Ван-дер-ваальсовой, электростатической, расклинивающей составляющими межчастичного взаимодействия, кинетической энергией присоединенной частицы. При значительной кинетической энергии частица может разрушить кластер или под действием свободной воды покинуть его зону. Частицы, не попавшие в такие кластеры, будут утолщать перемычку, т.е. тем самым способствовать увеличению плотности пенобетона или кольматировать поры. Кстати, правомерность перехода к двухфазной системе находит подтверждение, например,  в работах В.Н. Феклистова [15] по оценке формирования пенобетонной структуры различной плотности.

Предложенная схема позволяет сформировать подходы к математической модели процесса для изотермических условий. Для формируемой модели будем считать справедливыми, помимо изотермичности, требования  монодисперсности фаз, растворения и диффузии газа. Между введенными в рассмотрение выше фазами будем полагать действительными следующие массовые переходы: переход твердых частиц из жидкой фазы на газовый кластер (и наоборот); переход связанной жидкости в свободную (и наоборот). Присвоим несущей фазе индекс 1, а газотвердожидкостной - 2. Рассматриваем движение несущей фазы по капиллярно-пористой системе, в качестве которой будет выступать каркас из упакованных случайным образом кластеров с минимумом энергии их взаимодействия (подобная упаковка характерна для "легких" теплоизоляционных пенобетонов).

Выделим в исследуемой системе элементарный единичный объем  и для каждой из фаз составим:

- уравнения сохранения массы:

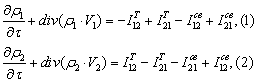
В уравнениях (1) и (2):  I₁₂^T - удельный поток твердых частиц из несущей фазы 1 на поверхность фазы 2; I₂₁^T - то же, но в обратном направлении; I₂₁^св - удельный поток связанной воды с пузырька в несущую фазу; I₁₂^св - то же, но в обратном направлении.

- уравнение изменения импульса несущей фазы 1:

где: V₁ и V₂ - векторы скоростей фаз;F₂₁ - межфазное трение;  ρ₁g - массовая сила.

Левая часть в уравнении (3) представляет инерционную силу от ускорения, действующего на фазу: V₁ = (V_1x , V_2y , V_3z). Первое слагаемое правой части определяет напряжения в фазе, второе - межфазное взаимодействие по внешним границам фаз и зависящее от (V₂ -V₁). Третье слагаемое учитывает действие гравитационных сил, а четвертое и пятое - прирост / убыль импульса фаз от присоединенных масс твердых частиц и связанной воды.

- уравнение изменения импульса фазы 2:

где: σ₂ - напряжение в дисперсной газотвердой фазе; F₁₂ - межфазное трение.

Последнее слагаемое в уравнении (4) характеризует прирост импульса за счет присоединенных масс.

Будем считать, что нестационарный режим истечения жидкости представляет собой совокупность микроравновесных состояний, то есть:

Так как движущей силой синерезиса жидкости является гравитационная составляющая  g, то целесообразно в дальнейшем ограничиться одномерным случаем (по оси Z). Поскольку индукционный период начинается после:  розлива пенобетонной смеси в формы; замедления действия инерционных сил, то ими в дальнейшем упрощении модели можно пренебречь (по сравнению с массовыми силами). Поскольку формирование кластеров обычно заканчивается на этапе приготовления пенобетонной смеси, то присоединенными массами твердых частиц к газовому пузырьку можно пренебречь. Также для упрощения пренебрегаем в математической модели эффектами физико-химической природы (электрокинетические явления, смачиваемость поверхностей и т.п.).

Система уравнений (1-4) после упрощений примет вид:

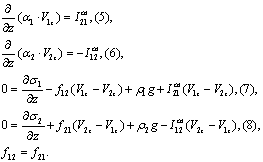
Последние слагаемые в уравнениях (7) и (8) являются приращениями импульсов фаз за счет перехода связанной воды из фазы 2 в вязкую жидкость фазы 1.

Для нахождения межфазного трения  f  можно воспользоваться зависимостью:

где: е = a₁ / a₂ - объемное соотношение фаз; S - удельная поверхность межфазного трения; а - коэффициент фильтрации при синерезисе.  Для ячеистой модели:

где: k - суммарная константа Козени-Кармана; μ - вязкость несущей фазы, которую можно определить по формуле Эйнштейна:

μ₁ = μ_ж (1+ 5a_тж/2a₁),

где:  μ_ж - вязкость жидкости;  a_тж - объемная доля твердой фазы в жидкости.

Напряжение в вязкой несущей среде определяется:

где:   δ^kl - символ Кронекера; τ^kl₁ - тензор вязких напряжений;  Р₁  - давление; е^kl₁ - тензор скоростей деформаций несущей фазы.

Напряжение в дисперсной фазе в общем виде:

Примеры компрессионной характеристики дисперсной фазы приведены, например,  в [16-19].

Для завершения формирования вышеприведенной модели необходимо добавить граничные условия, основываясь на данных:

- для верхней границы - скорость поступления свободной жидкости к верхней границе равна нулю, то есть V_1z = 0;

- на нижней границе раздела жидкости и пенной структуры концентрация дисперсной фазы минимальна, то есть a₂→ min.

Наши дальнейшие исследования по разработке модели предполагают анализ ее замыкания, получение численного решения системы дифференциальных уравнений для граничных условий, проведение экспериментальных исследований по анализу устойчивости модельных систем и сравнение полученных данных с теоретическими предположениями.

Данная работа выполнена в рамках тематического плана, финансируемого Федеральным агентством по образованию РФ в 2006 г., тема НИР: "Теоретические основы формирования пористой структуры в наполненных ячеистых бетонах".

СПИСОК ЛИТЕРАТУРЫ:

1. Тихомиров В.К. Пены. Теория и практика их получения и разрушения. М.: Химия, 1983.
2. Трапезников А.А. Некоторые свойства пленок и пен и вопросы их устойчивости. // Пены. Получение и применение. / Материалы Всесоюзной научно-технической конференции. Часть 1. Физико-химия пен.- М.: 1974. - С.6-37.
3. Канн К.Б. Некоторые закономерности синерезиса пен. // Коллоидный журнал.- 1978.- т. 40.- с.858.
4. Кротов В.В. Обобщенные уравнения синерезиса. // Коллоидный журнал.- 1984.- т. 4 - с.14.
5. Канн К.Б. Капиллярная гидродинамика пен. - Новосибирск: Наука, 1989.
6. Волков П.К. Гидродинамика всплывающих пузырей и капель: Автореферат дисс.... д-ра физ.-мат.наук:-Новосибирск, 1992. - 34 с.
7. Гудов А.М. Численное моделирование взаимодействия пузыря с различными типами границ в жидкости: Автореферат дисс... канд. физ.- мат. наук: - Кемерово, 1996. - 24 с.
8. Сахабутдинов А.Ж. Численное трехмерное моделирование динамики газового пузырька: Автореферат дисс... канд. физ.-мат. наук: - Уфа, 1999. - 19 с.
9. Кондратьев С.А. Развитие теоретической базы интенсификации процесса пенной флотации на основе оптимизации гидродинамики и физико-химических свойств поверхности раздела "газ - жидкость": Автореферат дисс... д-ра техн. наук: - М., 2002. - 36 с.
10. Хисматуллин Д.Б. Математическое моделирование резонансных явлений в динамике пузырьковых жидкостей: Автореферат дисс... канд. физ.-мат. наук: 05.13.16. -Уфа, 1998. - 23 с.
11. Кутателадзе С.С., Стырикович М.А. Гидродинамика газожидкостных систем. - М.: Энергия, 1976. - С.295.
12. Гегузин Я.Е. Пузыри - М.: Наука, Физматгиз, библ. «Квант», вып. 46. - 1985.- С. 177.
13. Островский Г.М. Прикладная механика неоднородных систем. - СПб.: Наука, 2000. - С. 359.
14. Островский Г.М., Некрасов В.А. Математическое моделирование процессов истечения жидкости из пен. // ТОХТ- 1966.- Т.30. - №6. - С.657 - 661.
15. Феклистов В.Н. К оценке формирования пенобетонной структуры различной плотности. // Строительные материалы. - 2002.- №10.- С.16.
16. Штакельберг Д.И., Сычев М.М. Самоорганизация в дисперсных системах. - Рига: Зинатне, 1990. - 175 с.
17. Федоткин И.М. Интенсификация технологических процессов. - Киев: Вища школа, 1979. - 342 с.
18. Федоткин И.М., Воробьёв Е.И., Вьюн В.И. Гидродинамическая теория фильтрования суспензий. - Киев: Вища школа, 1986. - 166 с.
19. Нигматулин Р.И. Динамика многофазных сред.- М.: Наука, 1987. - 360 с.

Работа представлена на заочную электронную конференцию «Новые технологии, инновации, изобретения», 15-20 июля 2006 г.

Библиографическая ссылка