Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Тимофеев И.А.

Статья в формате PDF

125 KB

Одной из главных задач, является контроль магнитных характеристик, немаловажным фактором является также контроль удельных потерь.

Если удельные потери имеют завышенные величины, то использование магнитных материалов в электротехнических устройствах имеет ограниченное применение или вообще становится нецелесообразным. Наиболее конкурентоспособным становится то электротехническое изделие, магнитномягкий материал которого имеет высокие магнитные свойства и низкие удельные потери.

Легирование кремнием, который образует с железом твердый раствор замещения, обусловливает увеличение удельного электрического сопротивления. Влияние кремния на удельное электрическое сопротивление определяется следующей приближенной эмпирической формулой [1]:

                .              (1)

Железокремнистые сплавы с низкими значениями удельного электрического сопротивления не находят широкого применения даже в технике низких частот из-за повышенных величин вихревых токов. На величину и направление вихревых токов, кроме размеров магнитного сердечника, влияют его удельное электрическое сопротивление, частота электрического тока и магнитная проницаемость. Соответственно вихревые токи, вызываемые перемагничиванием магнитных материалов, влияют на удельные потери.

Уточнение расчетной формулы

Современные формулы для подсчета удельных потерь дают определенные погрешности. Рассмотрим это на примерах.

Попытка произвести расчет удельных потерь на вихревые токи в ферромагнетике была предпринята в 1926 г. Б.А. Введенским [2]. Он предложил следующую формулу:

,                             (2)

где  d - толщина пластинки;

В_о - магнитная индукция, В_о=μ×Н_о;

ω - циклическая частота;

q - магнитная проводимость.

Однако формула (2) весьма приближенно определяет удельные потери на вихревые токи. Ошибки Введенского состояли в том, что значение магнитной проводимости q необходимо было ввести в числитель, а не в знаменатель. Кроме того, в числитель необходимо было ввести значение циклической частоты не в первой степени, а во второй, т.е. ω², а в знаменателе необходимо было учесть значение плотности материала.

Интерес к определению удельных потерь в магнитных материалах появился в связи с возможностью широкого их применения при создании горячекатаной электротехнической стали для электрических машин. После того, как в 1935 г. Госс [3] обнаружил высокие магнитные свойства у холоднокатаной электротехнической стали вдоль направления прокатки, интерес к изучению удельных потерь повысился. В последующие годы активизируются исследования по улучшению электрических характеристик стали.

Первое приближенное полуфеноменологическое уравнение для расчета полных потерь в проводящем ферромагнетике в 1937 г. дали Елвуд и Легг [4]:

 Р_полн. = ,                 (3)

где  В₀ - постоянная для данного сплава величина;

μ - магнитная проницаемость;

С - не зависящая от В_о и w величина.

Экспериментальная проверка показала, что ошибки Елвуда и Легга состояли в том, что кроме тех ошибок, которые были сделаны Введенским в приближенное полуфеноменологическое уравнение (3) необходимо было ввести значения плотности материала и коэрцитивной силы. Введенные параметры  и μ³ в уравнение (3) дополнительно искажают результаты расчета.

Приведенная формула (3) не учитывает дислокационную теорию магнитных свойств материалов. Более точную зависимостьопределения потерь энергии от физических величин при перемагничивании ферромагнетика дал Мишин [5]:

  ,      (4)

где    - магнитострикционная константа;

L - средняя толщина дислокационного сегмента;

δ - толщина доменной структуры;

в - вектор Бюргерса;

N - плотность дислокаций;

S - площадь смещающихся границ доменов;

n - число доменов в единичном объеме ферромагнетика.

В этой зависимости учтено поглощение энергии изгибающимися под действием упругого поля доменными границами с дислокационными сегментами, но не учтена гистерезисная составляющая потерь и не принято во внимание удельное электрическое сопротивление материала. Однако эта зависимость позволяет определять потери энергии от физических величин и не позволяет практически определять удельные потери на промышленных магнитных материалах в зависимости от технических величин.

Практическую формулу для инженерных расчетов удельных электрических потерь на вихревые токи предложил круг [6]. Он, суммируя множество замкнутых электрических контуров, учел потери по всем контурам и привел следующее выражение:

 Р_в= ,        (5)

где В_м - амплитуда магнитной индукции, Тл;

f -частота переменного тока, Гц;

d - толщина пластин, мм;

k_f - коэффициент формы кривой магнитной индукции;

γ - плотность материала пластины, кг/м³;

ρ - удельное электрическое сопротивление материала пластины, Ом×м.

Применяя формулу (5), результаты практических вычислений становятся заниженными в среднем на четыре порядка, т.е. в 10⁴ раз.

Однако, чтобы формула (5) была полностью представлена в системе СИ и соответствовала примерно реальным показателям по потерям на вихревые токи, необходимо подставить в формулу толщину пластин в метрах и упразднить коэффициент 10^-10, т.е.:

 Р_в=   .         (6)

Из работы Дружинина [1] известно, что потери на гистерезис пропорциональны площади статистического цикла гистерезиса, частоте перемагничивания и обратно пропорциональны плотности материала пластины, и определяются из следующего выражения:

 Р_г= 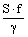,                              (7)

где S - площадь статического цикла гистерезиса, Тл×А/м.

Преобразовав петлю гистерезиса в виде прямоугольника, можно площадь статического цикла гистерезиса приблизительно определить по следующее простой формуле:

 S= 4В_м×Н_с,                           (8)

где Н_с - коэрцитивная сила.

Следовательно, удельные потери на гистерезис с учетом формулы (8) можно определить по следующей формуле:

 Р_r= .                    (9)

Определив составляющие потерь по формулам (6) и (9), можно найти общие удельные потери на перемагничивание магнитномягких материалов:

Р=Р_в+Р_г = 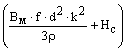, (10)

где Н_с - значение коэрцитивной силы приведено без учета плотности дислокаций и концентрации доменов.

На коэрцитивную силу на основе современной дислокационной теории магнитных свойств материалов оказывает влияние взаимодействие доменной и дислокационной структур. Для этого случая коэрцитивная сила может быть представлена в виде [7]:

Н_с=1,5 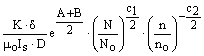,                        (11)

Здесь К - константа магнитной анизотропии; δ- толщина доменной стенки; μ₀ - магнитная постоянная, μ₀ = 4π×1 0^-7 Гн/м; I_S - самопроизвольная намагниченность; D - диаметр кристаллита; N - текущая плотность дислокаций; N_о - максимальная плотность дислокаций; с₁ - постоянная для отношения плотности дислокаций; n - текущая концентрация доменов; n_о - максимальная концентрация доменов; с₂ - постоянная для отношения концентрации доменов.

Следовательно, окончательно общие удельные потери с учетом формулы (11) можно представить следующей формулой:

 Р= 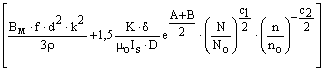.                          (12)

Удельное электрическое сопротивление магнитного материала является структурно чувствительной величиной поэтому запишем уравнение для зависимости удельного электрического сопротивления от плотности дислокаций и концентрации доменов в следующем виде с учетом уравнения (1):

                 (13)

где  в - коэффициент, в=0,1...0,9;

q - постоянная для отношения плотности дислокаций;

ε - постоянная для отношения концентрации доменов.

Таким образом, на удельное электрическое сопротивление магнитного материала существенно влияет взаимодействие доменной и дислокационной структур.

Вывод

Выведена расчетная формула удельных электрических потерь для магнитных материалов в зависимости от плотности дислокаций и концентрации доменов.

СПИСОК ЛИТЕРАТУРЫ:

1. Дружинин В.В. Магнитные свойства электротехнической стали. - М.: Энергия, 1974. - 239 с.
2. Введенский Б.А. ЖРФХО, часть физ. 58,241 (1926).
3. Goss N.P. New development in electrical strip steels characterized by fine grain structure approaching the properties of a single crystal. - TASM, 1935, VI, v. 23, № 2, p. 511-544
4. Elwood W.B., Legg V.E., J. Appl. Phys. 8, 351 (1937).
5. Мишин Д.Д. Магнитные материалы. - М.: Высшая школа, 1991. - 384 с.
6. Круг К.А. Основы электротехники. - М.-Л.: ОНТИ, 1936.
7. Тимофеев И.А. Современные наукоемкие технологии. - 2005. -№ 11. - С. 84-86.

Библиографическая ссылка