В современных условиях при разработке математических моделей широко используются принципы системного подхода, основными среди которых являются:
- принцип единства: совместное рассмотрение системы как целого и как совокупности элементов с позиции реализации общей цели;
- принцип связности: рассмотрение, как правило, количественно, любой части совместно с ее связями с окружением;
- структурное описание системы, построенное для большинства случаев по иерархическому принципу.
Математические модели оптимального управления ЛПУ должны реализовывать принципы системного подхода, учитывающие специфические особенности ЛПУ. Е.Н. Шиганом в 1982 году изложена методология системного подхода, произведена классификация методов системных исследований в области медицины в работе «Системный анализ в здравоохранении» [1, 2].
Изучению динамики процесса оказания медицинской помощи посвящено достаточно большое количество работ, отражающих те или иные аспекты этого сложного социально-психологического вида человеческой деятельности. При этом вопрос рассматривается с социальной, физиологической, медицинской и психологической точек зрения. Поэтому каждый вид исследования сопровождается созданием тех или иных формальных математических моделей, основанных на определенных допущениях, отражающих специфику данного исследования. В данном случае нас будет интересовать изучение процесса оказания медицинской помощи, а точнее одного из его видов - диспансеризация населения.
Диспансеризация работающих в разных областях экономики - это национальный проект «Здоровье», которым начинается новый важный этап развития здравоохранения. Углубленное обследование здоровья в 2006 году пройдут 4 млн. россиян, в 2008 - еще 8 млн. Авторы реформы считают, что диспансеризация станет реальным шагом на пути поворота нашего здравоохранения от «лечения болезней» к «сохранению здоровья».
Обязательные обследования, сходящие в состав диспансеризации на сегодняшний день: флюорография (для женщин и мужчин), осмотр гинеколога (для женщин), осмотр уролога (для мужчин старше 30лет), ВГД (для мужчин и женщин старше 40 лет).
Рассмотрим процесс диспансеризации как массовое вероятностное явление, основой моделирования которого служит теория случайных процессов. При этом процесс диспансеризации можно представить в виде последовательности случайных событий, переводящих объект из одного состояния в другое.
Введем следующие допущения:
- процесс перехода от одного этапа диспансеризации к другому происходит скачкообразно;
- вероятность перехода в каждое последующее состояние зависит только от предыдущего состояния (отсутствие последействия).
Эти допущения позволяют интерпретировать процесс диспансеризации как дискретную Марковскую цепь.
В процессе диспансеризации пациента могут произойти события:
А1 - пациент получает информацию о необходимости пройти обследование;
А2 - у пациента возникает желание (возможность) пройти обследование.
В результате пациент может оказаться в одном из следующих состояний:
S1 - пациент не знает о необходимости пройти обследование.
S2 - пациент знает и желает пройти обследование;
S3 - пациент знает и не желает (не может) пройти обследование;
S4 - пациент прошел необходимое обследование:
Рассмотрим приведенное множество состояний с точки зрения его структуры - возможности перехода из состояния Si в состояние Sj непосредственно или через другие состояния.
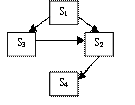
по оценкам экспертов переходные вероятности могут быть следующими
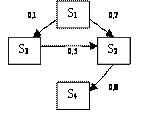
Состояние S4 является поглощающим, в каждом из состояний S3, S2, S1 система может «задерживаться». Обозначим S(t) состояние системы S в момент времени t. Вероятность i-ого состояния обозначим pi(t). Очевидно, что для системы с дискретными состояниями в любой момент времени ![]() .
.
Основной задачей исследования Марковской цепи является нахождение безусловных вероятностей системы pi(k)на любом k-м шаге. Для их нахождения необходимо знать условные вероятности pij(k) перехода системы s на k-м шаге в состояние sj, если известно, что на предыдущем шаге она была в состоянии si. Вероятность pii(k) - это вероятность того, что система «задержится» в состоянии sj. В предложенной системе существуют невозможные переходы s41, s14, s34,s31, s21, s23, s42, s43, s41. Следовательно, условные вероятности таких переходов равны 0. Матрица переходных вероятностей имеет вид
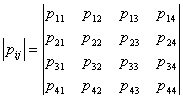
Сумма вероятностей по строке равна 1. Поскольку состояние системы S4 является поглощающим, следовательно, p44=1, p42= p43= p41=0. Условная вероятность перехода из состояния S2 в состояние S4 - p24 (физическая возможность пройти нужные обследования, если есть желание, т.е. возможность попасть, например, к нужному врачу, не тратя на это чрезмерных усилий), p23= p21=0. p11=1-(p12+ p13). P33=1- p32, p22= 1- p24.
Используя предложенные экспертами оценки составим матрицу переходных состояний.

 (1)
(1)
Применяя предложенную в [3] формулу для подсчета распределения вероятностей системы на k-м шаге:
![]() (2)
(2)
Так как в начальный момент времени система заведомо находится в состоянии s1, то p1(0)=1, p2(0)=0, p3(0)=0, p4(0)=0. Применяя предложенную выше формулу (2), найдем вероятности состояний. Результаты расчета вероятностей для переходных состояний, указанных в матрице (1) представлены в таблице 1.
Таблица 1. Распределения вероятностей состояния пациента при диспансеризации
|
шаг (k) |
Распределение вероятностей на k-м шаге по состояниям |
|||
|
s1 |
s2 |
s3 |
s4 |
|
|
0 |
1 |
0 |
0 |
0 |
|
1 |
0,20 |
0,70 |
0,10 |
0,00 |
|
2 |
0,04 |
0,33 |
0,07 |
0,56 |
|
3 |
0,01 |
0,13 |
0,04 |
0,82 |
|
4 |
0,00 |
0,05 |
0,02 |
0,93 |
Можно сделать вывод, что с возрастанием k, вероятность поглощающего состояния (пациент прошел необходимые обследования) возрастает.
Предположим, что вероятности переходных состояний значительно ухудшены, т.е. некоторые врачи принимают пациентов без необходимых обследований и число пациентов, не желающих проходить обследование, увеличится (матрица 3), то и тогда для k=4 вероятность поглощающего состояния не изменится (табл.2).
 (3)
(3)
Таблица 2. Распределения вероятностей состояния пациента при диспансеризации для матрицы 3
|
шаг (k) |
Распределение вероятностей на k-м шаге по состояниям |
|||
|
s1 |
s2 |
s3 |
s4 |
|
|
0 |
1 |
0 |
0 |
0 |
|
1 |
0,10 |
0,50 |
0,40 |
0,00 |
|
2 |
0,02 |
0,29 |
0,13 |
0,56 |
|
3 |
0,00 |
0,12 |
0,05 |
0,82 |
|
4 |
0,00 |
0,05 |
0,02 |
0,93 |
Однако, если предположить, что пациент знает о необходимости обследования и желает, но в силу объективных причин (нет врача или нет оборудования) вероятность перехода из состояния S2 в состояние S4 уменьшена (матрица 4), то вероятность поглощающего состояния значительно уменьшиться (табл.3).
 (4)
(4)
Таблица 3. Распределения вероятностей состояния пациента при диспансеризации для матрицы 4
|
шаг (k) |
Распределение вероятностей на k шаге по состояниям |
|||
|
s1 |
s2 |
s3 |
s4 |
|
|
0 |
1 |
0 |
0 |
0 |
|
1 |
0,20 |
0,70 |
0,10 |
0,00 |
|
2 |
0,04 |
0,54 |
0,07 |
0,35 |
|
3 |
0,01 |
0,23 |
0,04 |
0,73 |
|
4 |
0,00 |
0,09 |
0,02 |
0,89 |
Следовательно, одним из важнейших условий диспансеризации населения является наличие необходимого оборудования и достаточного количества врачей, и в меньшей степени наличие доброй воли пациентов. Этот вывод подтверждается уменьшением вероятности достижения поглощающего состояния (на шаге 2 - 0,35, на шаге 3 - 0,73, на шаге 4 -0,89), приведенных в таблице 3, в которой расчет производился для варианта, в котором вероятность перехода из состояния S2 в состояние S4 уменьшена, в то время как вероятности, приведенные в таблицах 1и 2, для расчета которых были использованы экспертные оценки, равны 0,56, 0,73, 0,93 соответственно.
СПИСОК ЛИТЕРАТУРЫ
- Шиган Е.Н. Системный анализ в здравоохранении. М.: ЦОЛИУВ, 1982, 70 с.
- Шиган Е.Н. Системный анализ в управлении здравоохранением: Руководство по социальной гигиене и организации здравоохранения./Под ред. Ю.П. Лисицына.-М.: Медицина, 1987, т.2, с.41-65.
- Вентцель Е.С., Теория случайных процессов и ее инженерные приложения: Учеб. пособие для студ. втузов /Е.С. Вентцель, Л.А. Овчаров. - 3-е изд., перераб. и доп. - М.: Издательский центр «Академия», 2003. - 432 с.
Библиографическая ссылка
Алмазова Е.Г., Микшина В.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ДИСПАНСЕРИЗАЦИИ НАСЕЛЕНИЯ // Успехи современного естествознания. 2006. № 11. С. 99-101;URL: https://natural-sciences.ru/ru/article/view?id=12214 (дата обращения: 25.02.2026).



