Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Гура П.С. Сысун В.И.

Статья в формате PDF

125 KB

Удержание плазмы магнитным полем (МП) является ключевым вопросом проблемы управляемых термоядерных реакций, неистощимого источника энергии. Однако и в других технических приложениях (лазеры, источники света, плазменные источники для покрытия и обработки поверхностей) удержание и отрыв плазмы от стенок позволяет существенно повысить параметры плазмы и технические характеристики устройств. При этом отсутствие необходимости полной изоляции плазмы от стенок в этих приложениях и существенно более низкие параметры плазмы снимают проблему появления большей части плазменных неустойчивостей и снижают требования к параметрам удержания. Часто достаточно лишь достичь значительного уменьшения концентрации вблизи стенки. В настоящей работе рассматривается возможность удержания плазмы модулированным продольным МП при наличии осевого разрядного тока в плазме [1].

Пусть продольное МП модулировано отрезками прямых (рис.1). Разрядный электронный ток направлен вдоль оси Z с электронной скоростью V_z . Рассмотрим равновесие плазмы в поперечном направлении r , считая изменение радиуса плазмы малым на периоде модуляции. Для удержания плазмы в среднем за период модуляции должно выполнятся соотношение:

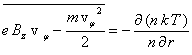,             (1)

где v_φ  - азимутальная холловская скорость электронов, уравнением для которой будет:

,                  (2)

где ν_e - частота электронных столкновений, - радиальная составляющая МП.

При постоянном B_r уравнение (2) есть линейное уравнение для v_φ и оно имеет решение:

 (3)

Отсюда видно, что v_φ  пропорционально , тогда можно положить:

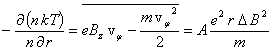,  (4)

где коэффициент А зависит от отношения  и параметров модуляции МП. Решением уравнения (4), при слабом изменении температуры электронов, будет:

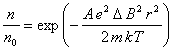,                    (5)

где n₀ - концентрация на оси.

Формула (5) даёт резкий спад концентрации по радиусу и, предполагая её значение на границе , можно определить необходимое для удержания значение  АDВ² :

.                  (6)

Рассмотрим конкретное значение коэффициента А.

При отсутствии столкновений, согласно (2), v_φ  определяется локальным значением магнитного поля (известная теорема Буша):

.

Тогда

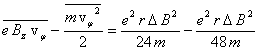  и  . 

Согласно (6) будем иметь: ; .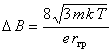

Таким образом, необходимая скорость превышает тепловую скорость, что приводит к бунемановской неустойчивости и турбулентности плазмы. При этом скорость v_j  ограничивается тепловой и удержание плазмы не достигается. Отметим, что постоянная составляющая магнитного поля В₀ не влияет на эффект удержания.

При большой частоте столкновений ;          .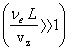

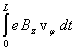  на участках нарастания и спада магнитного поля равен  и противоположен по знаку, так что его среднее значение на периоде равно нулю и А → 0.

Однако, при L₂ << L₁ возможен вариант, когда ограничение v_φ  тепловой скоростью будет только на участке расширения L₂ и тогда эффект сжатия на участке L₁ будет превышать эффект расширения на участке L₂ с суммарным сжимающим эффектом. Постоянная составляющая магнитного поля B₀ в этом случае может увеличить этот эффект сжатия. Действительно:

;

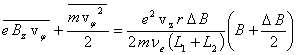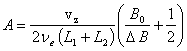
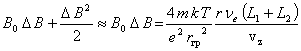
.       (7)

И условие v_{φ max} <  v_T    на первом участке равносильно условию:

4 r _eл < r _гр                                                                     (8)

где v_T    тепловая скорость электронов; 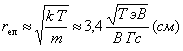- ларморовский радиус электрона в постоянной составляющей магнитного поля.

Таким образом, для удержания плазмы необходимо выполнение условий:

L₁ >> L₂ ;  ;   а также выполнение условий (7) и (8).

Экспериментальные исследования сжатия канала продольного разряда проводились нами для двух случаев распределения напряжённости магнитного поля вдоль оси трубки - модулированного магнитного поля с постоянной составляющей (рис.1) и знакопеременного магнитного поля (рис.2). Требуемая конфигурация и величина магнитного поля достигалась при протекании импульсного тока в плоских электромагнитных катушках, составляющих магнитную систему. Для обеспечения большей протяжённости участка нарастания магнитного поля по сравнению с участком уменьшения использовались ферромагнитные диски. Разряд зажигался в стеклянной трубке с внутренним диаметром 12мм в аргоне при давлении 0,05 ÷ 0.2 Торр.

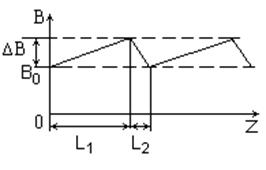
Рисунок 1. Распределение индукции магнитного поля, модулированного отрезками прямых, вдоль оси продольного разряда

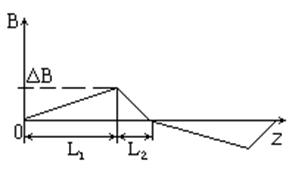
Рисунок 2. Распределение знакопеременного магнитного поля вдоль оси продольного разряда

Ток разряда имел прямоугольную форму, а магнитное поле практически постоянно во время горения разряда. Величина тока разряда варьировалась от 0,5А до 130А, а длительность импульсов от 0,2мс до 1мс. Максимальное значение индукции магнитного поля составляло 700Гс. Для регистрации эффекта сжатия канала разряда производилось фотографирование свечения канала разряда в промежутках меду катушками магнитной системы.

Полученные экспериментальные результаты можно свести к следующему:

- Особенно эффективно сжатие канала разряда в случае знакопеременного магнитного поля.

- Эффективность сжатия повышалась при уменьшении давления газа и с увеличением крутизны нарастания магнитного поля, которая определялась величиной тока в катушках и расстоянием между катушками.

- В плоскости прохождения B_z через нуль (реверс магнитного поля) наблюдалась яркая область свечения плазмы, достигающая стенок трубки. Воздействие плазмы в местах реверса магнитного поля на стенки усиливалось по направлению от катода к аноду.

- В режимах с эффективным сжатием в знакопеременном поле наблюдался существенный рост падения напряжения на разрядном канале, находящемся в магнитном поле.

- Сжатие канала разряда при тех же значениях тока в магнитных катушках проявлялось намного слабее в случае модулированного магнитного поля по сравнению с знакопеременным полем, однако, из-за локального выброса плазмы на стенку и наличия постоянной составляющей B_z , именно случай модулированного магнитного поля с постоянной составляющей представляется более перспективным.

Исследования, описанные в данной работе, были проведены в рамках проекта PZ-013-02, поддерживаемого совместно Американским фондом гражданских исследований и развития (АФГИР), Министерством образования РФ и правительством Республики Карелия.

Литература:

1. Сысун В.И., Хромой Ю.Д., Яковлев Д.В. и др. Авторское свидетельство СССР, №280772, 01.03.88. Дополнительное авторское свидетельство №324404, 10.03.91.

Библиографическая ссылка