ГРАВИТАЦИЯ: 1. ТЕОРИЯ БЕЗ СИНГУЛЯРНОСТЕЙ И «ЧЕРНЫХ ДЫР»
Методы подобия в механике и гидродинамике рассматривались в [7, 8]. Взаимная редукция математики, механики и физики - более общий подход. Возможна редукция отображения φ | DQ → Ф(R8) на структуру S тела элементарных частиц в октетной сигнатуре матрицы операторов [2]. Обратная редукция ψ из S тела элементарных частиц в гравитационную субстанцию 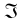 предполагает, что фрагмент физической картины мира «элементарные частицы» подобен фрагменту «гравитационное взаимодействие». По аналогии с углами смешивания для осцилляций частиц [9] строится локальная динамика смены гравитации (например, уровни Н1 и Н2 - тяготеющее состояние и индифферентное или отталкивающее состояние, соответственно [10], - получены в квазигамильтоновом приближении обобщенной механики). Произведено обобщение семи углов в R8, а именно:
предполагает, что фрагмент физической картины мира «элементарные частицы» подобен фрагменту «гравитационное взаимодействие». По аналогии с углами смешивания для осцилляций частиц [9] строится локальная динамика смены гравитации (например, уровни Н1 и Н2 - тяготеющее состояние и индифферентное или отталкивающее состояние, соответственно [10], - получены в квазигамильтоновом приближении обобщенной механики). Произведено обобщение семи углов в R8, а именно: ![]() , и операторов сложения / умножения:
, и операторов сложения / умножения: ![]() и
и ![]() , « + » и « * » и т.п. Восемь уравнений, описывающих осцилляции гравитации, в данном обобщении имеют вид:
, « + » и « * » и т.п. Восемь уравнений, описывающих осцилляции гравитации, в данном обобщении имеют вид:
|g+> = COSη1|f1> + SINη2|![]() >,
>,
|g-> = COSη2|f2> - SINη1| ![]() >, (a)
>, (a)
где антигравитирующие g+ и гравитирующие g- состояния и соответствующие им функции справа представлены в 4-векторном виде, f1, f2,![]() ,
, ![]() - состояния постэфирной материи (частиц), COS η, SIN η - функции смешивания, отличные от тригонометрических функций cos h, sin h.
- состояния постэфирной материи (частиц), COS η, SIN η - функции смешивания, отличные от тригонометрических функций cos h, sin h.
Теория {dzU = 0} / φ изоморфна теории ||dz|| U = 0, где матрица слева - латинский квадрат с восемью различными операторами [2]. Тригонометрические функции от углов смешивания (Кабиббо) записываются как операторы матрицы || ![]() ||, а совокупность состояний U рассматривается по фактору систематики частиц: U / S.
||, а совокупность состояний U рассматривается по фактору систематики частиц: U / S.
Некалибровочный вариант: || ![]() || (U/S) = G, где G - матрица состояний гравитации. Калибровочные варианты предполагают: 1) сохранение энергии всей (замкнутой) системы; 2) устранение физического времени Т (провремени). Тогда при g ∈ S и g ⊂ G прямая задача тоже корректна. Обратная задача описания частиц через состояния гравитации решается при || θ || ≠ 0 - если есть источники полей.
|| (U/S) = G, где G - матрица состояний гравитации. Калибровочные варианты предполагают: 1) сохранение энергии всей (замкнутой) системы; 2) устранение физического времени Т (провремени). Тогда при g ∈ S и g ⊂ G прямая задача тоже корректна. Обратная задача описания частиц через состояния гравитации решается при || θ || ≠ 0 - если есть источники полей.
«Спин» субстрата U / S зависит от времени жизни компонент, фрактален и определяет «спин» состояний гравитации. «Суммарный спин» локального гравитационного состояния - величина стохастическая. Так как генерация материи происходит в недрах массивных небесных тел с последующим ее распространением на периферию, «черных дыр» не существует. Ввиду рождения «ощущаемой материи» и, следовательно, всех ее взаимодействий преимущественно внутри тел, возможно наблюдение эффекта экранировки гравитации.
Сингулярных «точек», подобных полученной в решении уравнений ОТО (А.Фридман), в гравитации || ![]() ||(U/S) = G нет. Напротив, в ч. 4 статьи, как основное, аналитически рассматривается эфирное состояние Вселенной, аддитивное c физическими вселенными.
||(U/S) = G нет. Напротив, в ч. 4 статьи, как основное, аналитически рассматривается эфирное состояние Вселенной, аддитивное c физическими вселенными.
2. МНОГОЛИСТНАЯ ГРАВИТАЦИЯ В ПОСТ´ОКТЕТНОЙ МЕХАНИКЕ
Если U = - γmгпMга / r, где γ - аналог постоянной тяготения G в теории Ньютона, mгп - гравитационная пассивная масса тела, Мга - гравитационная активная масса центрального тела, r - расстояние между ними, то из (3"), см. ч. 1, получаем:
dr/dt = p(1 + gmгпMга / rm2иu2) / mи,
dp/dt = - rγmгпMга / r3, (1)
где γ = 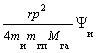 , ψи =
, ψи = 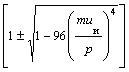 ,
,
где р - модуль импульса тела. Множитель при ψи при соответствующих значениях радиусов, масс и импульсов коррелирует с законами И. Кеплера для движения планет.
Из формулы γ = γ(xs, ps) получаем пять вариантов для решений системы (1):
|р| > ξ, (2)
|р| = ξ, (3)
|p| < ξ, (4)
где ξ = 2 ![]() mиu (вариант * : р = ±2
mиu (вариант * : р = ±2![]() jmиu, где j - любая единица алгебры октав, здесь не рассмотрен). В варианте (2) взаимодействие расслаивается: γ+= g1 + g2, γ- = g1 - g2. «Невозмущенная картина» из (3) - это γ0 =
jmиu, где j - любая единица алгебры октав, здесь не рассмотрен). В варианте (2) взаимодействие расслаивается: γ+= g1 + g2, γ- = g1 - g2. «Невозмущенная картина» из (3) - это γ0 = ![]() ru2 / Mга в рамках ньютонова приближения по тяготению квазиоктетной механики в гамильтоновом варианте. В случае (4) гравитация имеет две гармонические (осциллирующие в пространстве и времени) добавки:
ru2 / Mга в рамках ньютонова приближения по тяготению квазиоктетной механики в гамильтоновом варианте. В случае (4) гравитация имеет две гармонические (осциллирующие в пространстве и времени) добавки: ![]() =
= ![]() + i
+ i ![]() ,
, ![]() =
= ![]() - i
- i ![]() .
.
Таким образом, при |р| > ξ имеется два слоя взаимодействия, если |р| = ξ - квазиклассическое притяжение, при |р| < ξ - присутствует двойное волновое состояние. Чисто гармоническое взаимодействие: ![]() = ± i
= ± i ![]() ru2 / Mга, когда р = 0. Единица i =
ru2 / Mга, когда р = 0. Единица i =![]() - элемент С, отличный от единиц алгебры октав.
- элемент С, отличный от единиц алгебры октав.
В последнем случае тело, в начальный момент времени покоящееся в системе отсчета, связанной с центром гравитации, испытывает с ним только «волновое» взаимодействие - в отличие от феноменологической аппроксимации Ньютона. В этом проявляется давление волновой субстанции гравитационного «поля». Такова же ситуация при рождении вещества в кратерах звезд и после падения тела в центр гравитации. По мере «раскачки» вещества в недрах небесного объекта приобретается импульс, и тело покидает область рождения (фаза (4)). Затем тело проходит фазу (3) квазиклассического притяжения, медленно удаляясь в Космос. В фазе (2) материя «расщепляется» под действием антиподов γ+ ![]() γ-. Такова интерпретация ньютоновой формулы U =
γ-. Такова интерпретация ньютоновой формулы U = ![]() , где γ определяется по (2 - 4). Подстановка γ в систему (1) позволяет построить картину отклонений от классических теорий тяготения:
, где γ определяется по (2 - 4). Подстановка γ в систему (1) позволяет построить картину отклонений от классических теорий тяготения:
dr/dt = p(1 + р2/4mи2u2 ψи) / mи,
dp/dt = - rp2/4mиr2 ψи. (5)
В уравнениях (1) первые три из них отвечают поправке к инертной массе, зависящей от mгп, Mга. Уравнения (5) не зависят от гравитационных масс mгп, Mга. При переходе u → ∞исчезает зависимость и от инертной массы. Остается только фундаментальное беспричинное движение двух типов: 1) прямолинейное (называемое в феноменологии движением по инерции); 2) по экспоненте с расширением или сжатием - необратимость времени (из различимости уменьшения размеров объекта и их увеличения). Таким образом, даже при ньютоновом варианте тяготения в октетной и пост´октетной физике есть состояния (см. (3")), не зависящие от какой-либо из масс. То есть движение есть, а масс нет. Эфемерность массы означает, что масса - очередной флогистон.
При mu = 0 будет ψи = 1 ± 1, и второе слагаемое в первых 3-х уравнениях (5) равно ∞(+) или 0(-). При скорости передачи взаимодействия u > 0 в варианте 0(-) получаем: m = 0, dr/dt = ∞, dp/dt = 0, а в варианте ∞(+) имеем: m = 0, dr/dt = ∞, dp/dt = ∞. Если mu = 0 и m ≠ 0, то в варианте 0(-) в общем случае будет dp/dt ≠ 0, dp/dt = 0, а в варианте ∞(+) имеем: dr/dt = ∞, dp/dt ≠ 0. Эти случаи показывают, что взаимодействующее тело с m = 0 может находиться: 1) на ∞ и не испытывать действия сил с их источниками вблизи наблюдателя; 2) на ∞ и испытывать ∞-действие сил (сжатие пространства на оптическом горизонте в СТО, но с точки зрения наблюдателя), а невзаимодействующее тело с m ≠ 0 может находиться: 1) в состоянии расширения пространства, в котором оно существует, без действия сил; 2) на ∞ под действием эфемерных сил с их источниками рядом с неопозитивистом-наблюдателем. Третий случай обусловлен структурой свободного октетного пространства, приведенного, по А. И. Мальцеву: 1) на гиперсфере U 2 = R 2 ее фиксацией; 2) уравнением dU/dz = 0.
Решения (1) с учетом варианта * приводят к описанию многолистного гравитационного взаимодействия. Механизм переходов между листами (осцилляции гравитации) зависит от физики взаимных превращений частиц.
ТЕРМОДИНАМИКА
Реальная часть интервала в Q имеет вид * : ds2 = dt2 - dr2 - dH2 - dp2 - dφ2 - dψ2 - dΘX2 - ..., где для краткости опущены коэффициенты размерности и связи. Отсюда (для удельных величин) получаем ** : Тds = dr(dr/dt) + dh(dh/dt) + da(da/dt) + ..., где Т = γ - 1/γ, γ = 1/(1 - v2 - w2 - f2 - ...)1/2, dr/dt - скорость, w = dh/dt - плотность мощности, f = dp/dt - плотность (механической) силы, а - совокупность обобщенных параметров, da/dt - совокупность плотностей обобщенных сил, сопряженных а. Положим u = dh(dh/dt) - внутренняя энергия, dr - линейный объем, пропорциональный 3-объему dv, dr/dt - (среднеквадратическая) величина, пропорциональная (микроскопическим) вариациям объема dv, вызванных соударениями континуума точек (идеального) газа «со стенками», т.е. пропорциональная давлению р. Тогда, вводя аксиомы термодинамики:
АТ: Между формами * и ** существует простая редукция, сопровождающаяся переобозначением и умножением слагаемых на константы (размерности),
АТ1: Энтропия S подобна интервалу s системной физики (то же для дифференциалов этих функций),
АТ2: Температура Т подобна функции g - 1/g,
получим уравнение состояния системной термодинамики *** : Tds = u + pdv + Ada, где A = da/dt. Из этого вытекает, что системная физика является равновесной теорией. Поскольку из определенных вполне корректных предположений из * следует ***, а ds дефинирует состояние системы, то отсюда видно, что ПНД и лагранж-гамильтонов формализм в системном подходе - лишь частности. Относительно роли введенного понятия системной энтропии заметим, что уже в случае кватернионов скорость прямолинейного движения «точки» по инерции в фрактальном пространстве со временем падает по экспоненте (см. (2), с. 214 в [3]) до нуля (до минимальной скорости).
Имеем dS = a´ds, где [a´] = 1эрг/(1см*1К), Т = a"(γ - 1/γ), где [a"] = 1K, а слагаемые справа в *** умножаются на константу a"´: [a"´] = 1эрг*1с/1см. Энтропия АТ1 является инвариантом квазигруппы SU(n, Q), экстремальна при отсутствии любых изменений, процессов и развития системы и минимальна при ее максимально интенсивных в рамках размерности гиперкомплексной системы процессах. Температура АТ2 равна нулю при отсутствии каких-либо процессов, максимальна (стремится к бесконечности) при процессах, максимально интенсивных в данной (изолированной) системе, и инвариантом относительно SU(n, Q) не является. В этом состоит макроскопическая сущность октетной и системной параметризации. Однако в последовательном подходе интервал должен иметь "разрывы", обязанные несохранению числа частиц N макросистемы, количества ее микросостояний W и концентрации вещества r в интенсивных процессах (например, причиной этого могут служить появление адронных струй, аннигиляция и другие реакции ЭЧ).
Температура и энтропия в данном формализме не могут быть отрицательными величинами. Другие свойства величин, согласованных с определенными выше энтропией и температурой, можно получить из рассмотрения чисто гиперкомплексной части интервала. Решения системы уравнений биоктетной физики указывают на реверберацию автосолитона Метагалактики - без каких-либо предположений о том, что было до появления наблюдателя. То есть закон возрастания энтропии системной термодинамики содержится в аксиомах системной физики, в ее структуре, и связан с уменьшением амплитуды и с увеличением периода пульсаций проявленной части антропогенной вселенной [2]. Если температура и энтропия вводятся в системную термодинамику определениями, задающими их свойства на «границах применимости», то 1-е начало имеет то же статус, что и постулаты существования величин, входящих в интервал. Второе начало в системной термодинамике - теорема. Отсюда следует, что кроме параметрического времени t и семейства локальных времен {τ} существует идея времени, связанная со структурой аксиом системной физики и эксплуатацией ее теоремы - закона возрастания энтропии.
АТ3: Темп термодинамического времени {dt} является функцией температуры Т.
АТ3´: Существует термодинамическое время τ(ST) - комбинированное интровертное [2].
Основная теорема: При температуре Т = 0 энтропия S системной термодинамики является линейной функцией внешнего параметрического экстравертного экстенсивного времени t.
Действительно, равенство Т = 0 означает, что все термодинамические процессы в системе отсутствуют: γ = 1. Так как в этом случае ds = dt, то s = t + C (и S = t + C). Причем экстенсивный экстравертный априорный параметр t по отношению к интровертному комбинированному апостериорному термодинамическому времени τ(ST) является внешним. Поэтому в термодинамической теории можно положить S| T=0 = const (= 0).
Следствие 1: Третье начало термодинамики является теоремой системной физики.
Главная теорема: Энтропия S системной термодинамики самопроизвольных и равновесных систем не убывает.
Действительно, т.к. ds = dt/γ и γ > 0, энтропия среды для внешнего наблюдателя возрастает, поскольку «стрела» параметрического времени задается условием dt > 0. Для внутреннего наблюдателя, находящегося в равновесии с средой и измеряющего интровертное время τ(ST), ∂t/∂t = 0, т.к. τ и параметры системы явно от τ не зависят. Отсюда dτ = 0 и dS = 0.
Следствие 2: Второе начало термодинамики содержится в аксиомах системной физики, дополненных экстенциональными аксиомами:
АТ4: Существует мера близости r интровертного времени τ, определяемого в изолированной системе, и экстравертного времени t, определяемого в открытой системе.
АТ5: Существует мера l (для Т) изменения параметров частной системы s по отношению к общей системе Σ, характеризующая надсистемное время.
Такая «эргодичость» термодинамических систем устанавливает более общий смысл времени и она же его ограничивает. Здесь развитие теории времени возможно с привлечением теории меры, методов топологии, при варьировании 2-го начала по способам измерения входящих в уравнения экстенсивных и интенсивных величин.
Замечание: Температура Т = a"(γ - 1/γ) при постоянных малых значениях s (=ds) определяет термодинамическое время τ*. В кинематическом варианте при больших v (ввиду определения Т как функции от скорости) время τ* ~ t ~ γ. В системе отсчета, связанной с летящим телом, время в которой t´, отношение t´/t ~ 1/γ, т.е. t = t´ ![]() .
.
ПРОИЗВОДНЫЕ ТЕОРИИ
Пост´октетная механика уровня 1:
∂T/∂t = ĤH / m2u4 + ς,
dr/dt = gradp H - Ĥp / m2u2 - u2grad T ,
∂H/∂t = - μ2ĤТ ,
dp/dt = - grad H + μ2Ĥr / u2 - μ2m2u2gradpТ, (6)
где u - характерная скорость процесса, в системе, ς - мера необратимости провремени.
Пост´октетная механика уровня 2:
∂T/∂t = ĤH / m2u4 + ς,
dr/dt = gradp H - Ĥp / m2u2 - u2grad T ,
∂H/∂t = 0,
dp/dt = - grad H, (7)
где полная энергия не меняется со временем, μ=0.
Уравнения для быстрых процессов (частиц):
∂T/∂t =![]() А +
А +![]() Р,
Р,
∂А/∂t = - u( ![]() А -
А - ![]() Р + u
Р + u ![]() T),
T),
∂H/∂t = u2(![]() P - μ2m2
P - μ2m2![]() A)
A)
∂P/∂t = u( ![]() P + μ2m2
P + μ2m2 ![]() A - μ2m2u
A - μ2m2u ![]() T), (8)
T), (8)
где u → ∞,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() - обобщенные операторы по координатам и импульсам Дивергенции, Ротора, Градиента.
- обобщенные операторы по координатам и импульсам Дивергенции, Ротора, Градиента.
Уравнения для медленных процессов (частиц):
∂T/∂t = ĤH / m2u4,
∂А/∂t = - Ĥp / m2u2 {+ ![]() H }
H }
∂H/∂t = {- μ2ĤТ },
∂P/∂t = μ2ĤA / u2 {- ![]() H}, (9)
H}, (9)
где u → 0, а операторы и функции в фигурных скобках - расширение теории.
ПРИМЕЧАНИЯ К ТРЕМ ЧАСТЯМ СТАТЬИ
Термины «октетная физика», «биоктетная механика» и т.д. вводятся на тех же основаниях, что и термины «математическая физика», «статистическая физика», «фрактальная физика» и т.п., - за определением в терминах стоит соответствующий математический аппарат (см. [1 - 5]).
Гиперсфера U*U в О задана уравнением: U02 - U12 - ... - U72 = R 2. Для существования уравнений движения и состояний физики О необходимо постоянство размеров и формы гиперсферы U 2, но не имеет значения, какие локальные натяжения, деформации, потоки и процессы имеются в 7-мерном касательном слое к U 2 в каждой ее «точке» или протекают глобально, на всем ее «глобусе» (условие существования мира явлений - неизменная сущность отношения «субъект - объект»).
Число ς = 6 имеет топологическое происхождение, так как является суммой размерностей координатного пространства Vr и импульсного пространства Vp. То есть как только дополнительно к измерению времени t «появляются» другие, пространственные измерения, так сразу же возникает явление необратимости t. В биоктетной механике наряду с Vr , Vр рассматриваются пространство момента импульса Vrр и пространство момента силы Vrf , и поэтому ς = 12. Такое «теоретическое» повышение степени необратимости времени связано с учетом явлений поглощения и испускания различной радиации при изменении ускорения и ориентации частиц. Поэтому при росте массы (4-е уравнение в (1)) в поле тяжести U = - α/r при t > 0 имеем (I): ∂h(t)/∂t = (-a/r + h(t)) (C + ςt), а при t < 0 будет (II): ∂h(-τ)/∂t = (a/r - h(-τ)) (C - ςt), t > 0. Отсюда видно, что при левой ориентации аксиальной составляющей в С первое уравнение энергетически более выгодное (по модулю изменений), чем второе. То есть физическая система стремится к нарушению РТ-четности. При t > 0 и t ≈ 0 излучению энергетически выгодно иметь левую ориентацию (ср. с преобладанием левого нейтрино в солнечной радиации, что указывает на креатистское происхождение звезд и на источник их энергии в провремени, см. также об источнике энергии звезд сообщение Н.А.Козырева [6]).
Если изучается микро- или мегаобъект и сохраняется отброшенное слагаемое первого уравнения системы (4) в [3], то показатель асимметрии физического мира будет иметь вид: ς = ĤН/mи2u4 + ς, а постоянная С может изменить свою зависимость от обобщенных координат; в этом случае появляются дополнительные нюансы в теориях необратимости параметра t, нечетности Vr и несохранения РТ-четности. Данная асимметрия «поддерживается онтологически»: при отражениях t → - t, xs → - xs меняется вид систем уравнений типа (3, 4) в [3], что можно связать с необходимостью «брать энергетический барьер», обусловленный изменением топологии. Вообще, предполагается, что существует два взаимодополнительных подхода к интерпретации решений систем уравнений - первый: а) координаты вектора r в Vr (и вектора p в Vp) относятся к собственно пространству Vr (к Vр), а не к какому-либо конкретному (пробному) телу в нем (в Vр); б) компоненты вектора r координатного пространства Vr (или вектора импульса р в Vp) относятся к материальному (пробному) телу, «помещенному» в пространство Vr (в Vр), и в этом случае механика имеет дело с проявленной и «сгустившейся» материей, с конденсатом; второй: по возможности в исследованиях решений систем дифференциальных уравнений устраняется представление о ковариантности физических законов, связанной с линейными преобразованиями обобщенных координат (кроме, возможно, отражений). Это допускается, во-первых, потому, что в природе, по большому счету, нет ковариантности, особенно в том виде, который широко обсуждается при построении теорий над множествами ассоциативных элементов (любые преобразования координат - это умозрительная фикция; в объективном физическом мире для осуществления этой фикции требуются определенные усилия и мощность, но все реальные действия в общем случае некоммутативны и неассоциативны, т.е. теорема Э.Нетер об инвариантах, базирующаяся на теоретико-групповом подходе к проблеме геометризации физики, в общем случае не выполняется), а во-вторых - по причине того, что система (всех) координат мысленно ориентирована, растянута, деформирована, вращается, если это допустимо по смыслу задачи, подвергается переносам с изменяющимся ускорением и т.д. произвольным образом сама еще до «привнесения в нее» объектов изучения. Зато объекты изучения в «зафиксированной» произвольно выбранной системе координат (системе отсчета) «ведут себя» произвольно, но по установленным правилам поведения. Таким образом, меняются и выводы о симметрии или асимметрии состояний и процессов, описываемых с помощью представлений квазигрупп, и выводы о плодотворности идеи ковариантности.
В «современной» теоретической физике, в частности в ОТО, априорное принятие какой-либо локальной калибровочной симметрии требует затем введения определенного конкретного взаимодействия (гравитационного). В октетной физике экспериментальное обнаружение определенной локальной калибровочной симметрии (или асимметрии) приводит к апостериорным теориям взаимодействий. Таким образом, на первый план выступают не воображаемые взаимодействия с целью подогнать их под фантастику частных симметрий, но построение картины взаимодействий на эмпирическом фундаменте наиболее общих симметрий и нарушения или отсутствия частных симметрий.
Вид функции h(t) получен на первом шаге рекуррентного процесса в приближении ĤН/mи2u4 = 0. Далее, учитывая уравнение ∂Т/∂t = ĤН/mи2u4 + ς, полученная функция h(t) подставляется в Ĥ и Н, затем определяется новая, скорректированная зависимость Т = Т(t, x, y, z, px, py, pz) и решается 4-е уравнение системы, и т.д.
Уравнения 1 и 5 системы (3) в [3] в наших приближениях допускают разрешение относительно функции h(t). Дифференцируя 5-е уравнение по t и подставляя в него значение ∂Т/∂t из 1-го уравнения, придем к интегро-дифференциальному уравнению:
 ,
,
которое бигармоническое, существенно нелинейное (т.е. имеет автосолитонные решения и не только их). В развернутом виде после некоторых сокращений
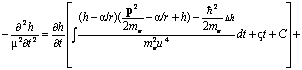
 ,
,
где Ĥ = - ( h2/2mи)Δ - α/r + h(t), ς = 6 - показатель необратимости провремени Т, определяемый размерностью пространств Vr ,Vр ...
Аксиоматика классической квантовой механики (в ее центральных утверждениях) выбирается независимо от аксиоматики ОТО. Квантовать ОТО - это скрещивать ужа и ежа, или «более научно»: это подобно тому, как в геоцентрической системе Птолемея объясняется реальное движение планет и Солнца «нанизыванием» на их круговые орбиты все новых «сфер обращения». В «квантовой гравитации», базирующейся на паллиативной квантовой механике и ассоциативной теории сингулярной точки - ОТО, нет фундаментальной объединяющей идеи, т.е. содержательного основания. Над тяжелым мышлением механистических квантистов все еще висит обоюдоострый «дамоклов меч»: 1) классической механики с ее законами сохранения; 2) принципа наименьшего действия. Более того, уравнение Шредингера, являющееся, в сущности, расщеплением над комплексным полем С очень частного случая уравнения Колмогорова - Чепмена в теории марковских процессов, построено по аналогии с приближением геометрической оптики на базе аксиомы «отсутствия памяти» системы: ∂ψ/∂t ~ aψ, т.е. принимается, что изменение волновой функции определяется только ее значением в настоящий момент времени. Тем самым вводится этакая «броуновская забывчивость» для мира, инертная масса в котором является синонимом памяти. Все очарование таких теорий состоит, по-видимому, в том, что сначала в них постулируется отсутствие способности искать и находить причинно-следственные связи во времени, а затем на основе их теорем удовлетворяются глубинные потребности субъекта в тайнах и волнующих душу «вероятностных» гаданиях. При этом «расщепленная вероятность» - волновая функция используется не в качестве основы для изучения потенциала упругих натяжений квантовой субстанции, а как цифровой гороскоп. Нормировка волновой функции упускает фазовые множители и, кроме того, нивелирует амплитуду гармонических потенциалов: нет ни порядка наступления событий, ни интенсивности перехода между ними - метафизическая данность мира, как таковая. Но даже в постгамильтоновой механике гравитационную и инертную массы необходимо рассматривать как результат эволюции материи от начала ее рождения до современной космологической эпохи. Между тем «квантовать» (вводом волновой функции под действие обобщенного оператора Гамильтона и под гамильтониан) уравнения октетной физики в общем случае не надо: волновой характер движения в них заложен уже при рождении материи.
Нижний уровень bC ~ kBT, где Т - температура Гамова. Отсюда (1 - ![]() )α/2r ~ kBT и b(kBT) ~ 5.7668.105 Дж/с. Характерно, что «средний уровень» b(kBT)/VМг ~ 2.9578.10-75 Дж/c, где VМг - объем пространства под оптическим горизонтом, а планковское значение bPl ~ 3.1321.10-70 Дж/c. То есть для разных тел (для различных задач) удельная мощность имеет разные значения.
)α/2r ~ kBT и b(kBT) ~ 5.7668.105 Дж/с. Характерно, что «средний уровень» b(kBT)/VМг ~ 2.9578.10-75 Дж/c, где VМг - объем пространства под оптическим горизонтом, а планковское значение bPl ~ 3.1321.10-70 Дж/c. То есть для разных тел (для различных задач) удельная мощность имеет разные значения.
Инертная масса тахионов, обеспечивающих эффект гравитации, «безопасна» для вещества, т.к. тахионы ввиду свойств октетного пространства с вероятностью р » 1 его огибают, не сталкиваясь [3]. В ОТО данное фундаментальное свойство физического пространства названо эффектом искривления луча света при прохождении вблизи массивных небесных тел.
ЛИТЕРАТУРА
- Верещагин И.А. Введение в октетную физику // Связь времен, в. 4. - Березники: ТКТ, 1997, с. 50.
- Верещагин И.А. Волны гравитации // Связь времен, в. 5. - Березники: ПрессА, 1998, сс. 44, 49, 60, 78, 96, 111 - 115.
- Верещагин И.А. Гиперкомплексная физика // Связь времен, в. 3. - Березники: ТКТ, 1996, сс. 88, 91, 186, 189, 215, 218 - 222.
- Верещагин И.А. Биоктетная механика // Связь времен, в. 6. - Соликамск: СТ, 1999, сс. 16, 106, 117.
- Верещагин И.А. Тахионы и масса // Связь времен, в. 7. - Березники: ДС СФЕРА, 2000, с. 70, 73.
- Козырев Н.А. // Изв. Крым. астр. общ., т. 2, в. 1, 1948.
- Седов Л.И. Методы подобия и размерностей в механике. - М.: Гостехиздат, 1957.
- Birkhoff G. Hydrodynamics. - Princeton: Univ. Press, 1960.
- Bilenky S.M., Pontecorvo B. // Phys. Rep., 1978, v. 41. P. 225.
- Верещагин И.А. Два уровня гравитационного взаимодействия / Тезисы докладов 11 Российской гравитационной конференции. - Томск: Изд. ТГПУ, 2002.
Библиографическая ссылка
Верещагин И.А. ПОСТЭФИРНАЯ ГИПЕРСИММЕТРИЯ ВСЕЛЕННОЙ. ЧАСТЬ 3 // Успехи современного естествознания. 2004. № 6. С. 11-16;URL: https://natural-sciences.ru/ru/article/view?id=12763 (дата обращения: 14.02.2026).



