В основе вычислений параметров у исходной конструкции идентифицируемой модели [1] лежат методы случайного поиска. По мнению проф. Л.А. Растригина [2, с.405] методы случайного поиска являются прямым развитием метода «проб и ошибок», когда решение принимается случайно. При удаче приближения выходных результатов математической модели к результатам объекта исследования решение оставляется, а в ином случае - отвергается. Случайность поиска становится источником возможностей.
Наше уточнение состоит лишь в том, что сама случайность является проявлением неизвестной биотехнической закономерности. Поэтому поиск при случайных вариациях значений и состава параметров модели в программной среде типа CurveExpert-1.3 внутри ПЭВМ ведется закономерно итерациями (сеансами) от простого к сложному в конструкции модели. Постепенно, в ходе структурно-параметрической идентификации и эвристического осмысления получаемых результатов, происходит наращивание модели. Она структурируется по типу - от простого фрагмента биотехнического закона к сложной аддитивной структуре волновых составляющих с переменными амплитудами и частотами колебаний у готовой статистической модели.
Пусть функционирование объекта описывается математической моделью вида
, (1)
где y - показатель (критерий) функционирования по выходному результату математической модели, x - множество объясняющих факторов (переменных), A - параметры модели, требующие определения.
Для модели (1) пусть известна исходная информация 
и 
по регистрации данных функционирования объекта исследования. Тогда задача идентификации сводится к задаче нелинейного программирования. Критерием качества (параметрической верификации) принимается сумма квадратов остатков, то есть
, (2)
где K - целевая функция минимизации остатков, n - общее число наблюдений.
По модели (2) параметры А исходной модели принимаются за независимые переменные. При этом имеем множества
, (2а)
. (2б)
При этом справедливо соотношение, что 
,(3) где 
- остатки между выходными результатами объекта исследования и его модели.
Сущность поиска значений множества 
сводится к тому, чтобы свести остатки к минимально возможным значениям пори постепенном наращивании фрагмента биотехнического закона до полной конструкции. Затем происходит переход к следующей аддитивной составляющей.
Адекватность модели оценивается по остаткам, которые принимаются как единицы статистической совокупности. Средняя арифметическая остатков будет равна
. (4)
При 
получим улучшение сходимости модели к фактическим данным.
Процедурная модель параметрической идентификации в специализированной программной среде РЕК (до 1600 точек, 25 факторов и 40 параметрах модели) приведена на рис. 1.
Рис. 1. Процедурная модель параметрической идентификации математической модели случайным поиском значений параметров
Из схемы видно, что исходная модель предполагается заданной, то есть до параметрической идентификации проведены этапы концептуальной и структурной идентификации моделей в виде эвроритмов. Процедурой 17 завершается создание готовой модели, которая в дальнейшем направляется для исследования влияния объясняющих переменных x на показатели y . После такого исследования проводится обратная идентификация объекта исследования по модели, то есть выводы и рекомендации, полученные после моделирования и исследования готовой модели, внедряются в производство и учебный процесс с целью улучшения процесса функционирования объекта исследования. Так происходит итерация исследований. Процедуры 3, 8 и 12 выполняются исследователем на ЭВМ. Для этого была разработана программа ПЭК(РЕК), полностью отражающая содержание процедуры 3. Все остальные процедуры выполняются вручную, то есть в неавтоматизированном режиме. Причем процедуры 5, 6, 7, 9, 12, 13, 16 требуют применения эвристик. Например, процедура 13 предполагает два случая: а) изъятие малозначимых факторов и соответственно их массивов данных; б) трансформация (чаще всего в сторону упрощения) частных функций, что не приводит к изменению массива исходных данных. В первом случае далее выполняется процедура 15, а во втором - деятельность исследователя направляется к процедуре 7.
Сходимость модели по процедуре 7 оценивается по снижению статистических показателей остатков, сравненных относительно выходных результатов объекта по данным блока 4.
Сходимость считается удовлетворительной, если происходит «рысканье» статистического показателя точности относительно некоторого минимально достигнутого значения. Если такой тремор наблюдается, то исследователь переходит к выполнению процедуры 8, иначе к процедуре 12, в котором корректируются параметры гипер-параллелепипеда выбора стартовых значений 
.
Уравнения для расчета статистических показателей остатков приведены далее. При высокой адекватности возможно исключение тех наблюдений, которые отклоняются от границ доверительного интервала наблюдений. Причем в процедуре 16 выполняется содержательный анализ причин «аномальных» отклонений. Если дополнительные факторы выявить невозможно, то исследователь переходит к процедуре 11.
От процедуры 16, если найдено объяснение отклоняющимся точкам, возможно два случая:
а) отбросить резко отклоняющиеся точки и перейти к 15;
б) найденное содержательное объяснение выразить в виде дополнительного фактора с его частной функцией и затем перейти к процедуре 13 с целью усложнения структуры математической модели.
Из схемы на рис. 1 видно, что чем лучше подготовлена конструкция исходной модели, то тем быстрее происходит процесс перехода к готовой модели. Чем больше число факторов х, то тем труднее мысленно охватывать конструкцию модели, поэтому здесь необходимо выполнять принципы поискового иерархического проектирования конструкции (в данной книге не рассматривается), например, по методике [3].
Алгоритм поиска параметров модели. Инструмент параметрической идентификации находится в процедуре 3 по схеме на рис. 1, реализованный в виде программы ПЭК. В процедурах 8 и 11 нами использовались стандартные известные программы.
Практически сеанс автоматического поиска содержит 5-15 циклов, а в каждом цикле принимается 300-2000 шагов поиска (в зависимости от числа факторов, числа наблюдений, а также заданного лимита машиносчетного времени). Программа ПЭК используется в итеративном режиме расчетов на ПЭВМ, что облегчает использование вычислительной машины и позволяет, в перерывах между сеансами, без спешки обдумывать эвристические приемы в соответствующих процедурах по схеме на рис. 1. В диалоговом режиме практически на ПЭВМ возможна идентификация только относительно небольших моделей, сущность которых и выходной результат (готовая модель) уже априори предугаданы. Диалоговый режим эффективен для идентификации функционирования различных объектов. В математической среде «Эврика» для ПЭВМ возможна идентификация регрессионных моделей с числом наблюдений до 24 и числом факторов до 4 (версия 1.0 Eureka).
После завершения каждого цикла на печать или на дисплей выводятся значения: 
. Здесь: 
- улучшенные значения параметров модели, приведшие к приближению ; 
- число заданных шагов поиска;
- число удачных шагов поиска; 
- сумма квадратов отклонений (остатков);
- среднеквадратичное отклонение; 
- ошибка среднеквадратичного отклонения; 
- показатель изменчивости остатков относительно выходных результатов объекта исследования;
- показатель точности (риска) сходимости модели относительно выходных результатов объекта исследования (100 - -доверительная вероятность математической модели); 
- относительное отклонение (относительная погрешность) выходных результатов объекта и модели y .
От цикла к циклу происходит изменение 
при . Первые (стартовые) значения выбираются случайно в некотором гипер-параллелепипеде.
, (5)
где a,b - границы интервалов, задаваемые ориентировочно, N - общее число параметров модели. В программе РЕК для ПЭВМ принимались просто некоторые значения 
, которые исследователю кажутся правдоподобными.
Внутри цикла поиск продолжается при снятых ограничениях (5). В последующих циклах в целях расширения стартовой области поиска принимается
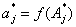и 
. (6)
Например, для автоматического переключения конфигурации гипер-параллелепипеда в стартах последующих циклов (после первого) поиска принимались
и 
. (6а)
После коррекции гипер-параллелепипеда новые значения 
снова случайно принимаются по условию (5). С учетом итераций по формулам (5) и (6) от цикла к циклу меняется область задания старта исходных значений параметров модели. Поэтому происходит псевдоглобальный поиск значений параметров математической модели (1).
Для решения задачи (2) совместно с В.Г. Грудачевым был предложен алгоритм случайного поиска в «несвязных» подпространствах, имеющий линейную тактику поиска. Случайный шаг выполняется после предыдущего неудачного, а в случае удачи шаги повторяются в одном и том же направлении.
Отличие этого алгоритма от известных алгоритмов случайного поиска [4, с.236-239] заключается в способе выбора приращений. Случайно выбирается целое число S, распределенное на отрезке [1,N] и определяющее количество одновременно изменяемых параметров модели. Номера которых определяются также случайно. Предложенный алгоритм случайного поиска можно записать в виде следующих рекуррентных выражений:
, (7)
при 
, (8)
где h - число последовательно неудачных шагов поиска.
Синтез приращений 
происходит следующим образом:
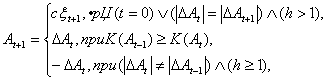(9)
где: 
, 
, - векторы приращений соответственно на t-1-м, t -м, t+1 -м шаге поиска; K(A t-1), K(A t) - значения критериев идентификации после осуществления t-1 и t шагов поиска; c - вектор максимального рабочего шага поиска, c={c j} ;
- (10)
вектор случайных чисел, равномерно распределенных на отрезке [-1;-u;u;1] ; u -коэффициент, учитывающий минимально допустимое значение длины рабочего шага, в нашем случае принималось u =0.001; p - случайный номер параметра математической модели, упорядоченный в интервале [1;N] соотношением, при s=1,N ,
. 
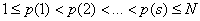(11)
Первые (стартовые) значения параметров математической модели задаются или случайным образом выбираются в заданной стартовой области поиска (5) с помощью соотношения
, (12)
где V j - вектор случайных чисел в интервале [u,1] .
Массив исходных данных (процедура 2 по схеме на рис. 2) включает: массив значений объясняющих факторов 
и выходных результатов 
объекта исследования, массивы границ стартовой области поиска a j и b j , массив вектора максимального рабочего шага поиска c j , а также значения числа наблюдений n , границ структуры математической модели N и m , границ сеанса поиска l (число циклов) и цикла h 0 (число принятых шагов поиска).
О второго цикла поиска значения вектора максимального рабочего шага вычисляются по формуле
. 
(13)
для которого мы принимали α = 0,1.
Анализ сходимости и адекватности модели. Случайность признана жизненным атрибутом любого явления [5, с.12]. Регрессия - это односторонняя стохастическая зависимость, выраженная с помощью функции [5, с.15]. В регрессионном анализе исследуется форма связи. А в корреляционном анализе - сила стохастической связи [5, с.18]. Если структура регрессионной модели подобрана верно, то необходимость в корреляционном анализе в методике МЭРА отпадает.
Сила связей между факторами определяется на основе исследования готовой модели.
Сходимость - это свойство приближаемости теоретической линии регрессии к выходным результатам объекта исследования. Критерием для оценки сходимости является время поиска параметров модели, или общее число шагов поиска по всем сеансам. Поиск прекращается после того, как сходимость модели по значениям её параметров прекращается, что можно оценить уменьшением остатков. Если остатки после нескольких циклов поиска начинают колебаться около одного и того же значения, то поиск прекращается. Далее по конечным остаткам оценивается адекватность модели процессу функционирования объекта исследования.
Такой подход эффективен для решения многих экономических задач. Как отмечается в работе [5, с.154], множественная нелинейная регрессия лучше отражает многообразие связей в экономике. Применение ПЭВМ с высоким быстродействием и большой памятью снимает все вычислительные проблемы, которые раньше были препятствием для создания нелинейных многофакторных моделей.
При применении метода наименьших квадратов (МНК) к оценке адекватности готовой модели к функционированию объекта исследования (а промежуточные значения показателей МНК - к оценке сходимости) будем считать, что стратегия, выбирающая наиболее эффективную проверку, всегда оптимальна. Такая эффективная проверка существует в общей теории статистики [68], в соответствии с которой ниже приведены расчетные показатели анализа адекватности выходных результатов готовой математической модели и объекта исследования.
Из сходных предпосылок получим формулу для расчета остатков
,(14)
где - выходной результат объекта (фактические значения показателя), y i - выходной результат математической модели (теоретические значения показателя), i - номер наблюдения, n - общее число наблюдений.
Причем теоретическое значение показателя оценивается по формуле (1). Все значения остатков образуют статистическую выборку для следующей составляющей искомой модели при условии, что данная составляющая доведена по сложности конструкции до полной структуры по биотехническому закону как по амплитуде, так и по половине периода колебательного возмущения.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико-математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100 с.
- Растригин, Л.А. Системы экстремального управления / Л.А. Растригин. - М.: Наука. 1974. - 632 с.
- Капустян, В.М. Конструктору о конструировании атомной техники / В.М. Капустян, Ю.А. Махотенко. - М.: Атомиздат, 1981. - 190 с.
- Автоматизация поискового конструирования (искусственный интеллект в машинном проектировании) / Под ред. А.И. Половинкина. - М.: Радио и связь, 1981. - 344 с.
- Фёрстер, Э. Методы корреляционного и регрессионного анализа: Руководство для экономистов / Э. Фёрстер, Б. Рёнц. - М.: Экономика и статистика, 1983. - 302 с.
Библиографическая ссылка
Мазуркин П.М. БИОТЕХНИЧЕСКИЙ ЗАКОН, ЭВРОРИТМ И АЛГОРИТМ ПОИСКА ПАРАМЕТРОВ // Успехи современного естествознания. – 2009. – № 9. – С. 88-92;URL: https://natural-sciences.ru/ru/article/view?id=12837 (дата обращения: 04.12.2024).